弓形截面螺旋半管夾套內流體流動與換熱

李雅俠, 欒 蘭，吳劍華

（沈陽化工大學 能源與動力工程學院， 遼寧 沈陽 110142）

反應釜是工業生產中的典型設備，通常釜內的反應過程會伴有放熱和吸熱發生，然而嚴格的溫度控制對于產品質量至關重要，此種情況下，反應釜需要配有傳熱裝置來確保最佳的工藝反應條件以便取得最好的反應效果。常采用的傳熱方式是在釜外安裝夾套或釜內設置蛇管的方式。而前者是優先選用的方式，主要是因為此種方式能夠減少容器內構件，便于清洗而且不占有效容積。在各種形式的夾套中，螺旋半管夾套憑借節省材料、承載能力強、傳熱效率高等優點越來越受到青睞[1]，按照其橫截面結構不同，可分為橫截面為半圓形和弓形的螺旋半管夾套，如圖1所示。

目前對于螺旋半管夾套的研究主要集中在橫截面為半圓形的夾套上，如：Dhotre[2]和Jayakumar[3]采用實驗方法對單一結構的螺旋半圓管夾套內流體的宏觀傳熱特性進行了研究；

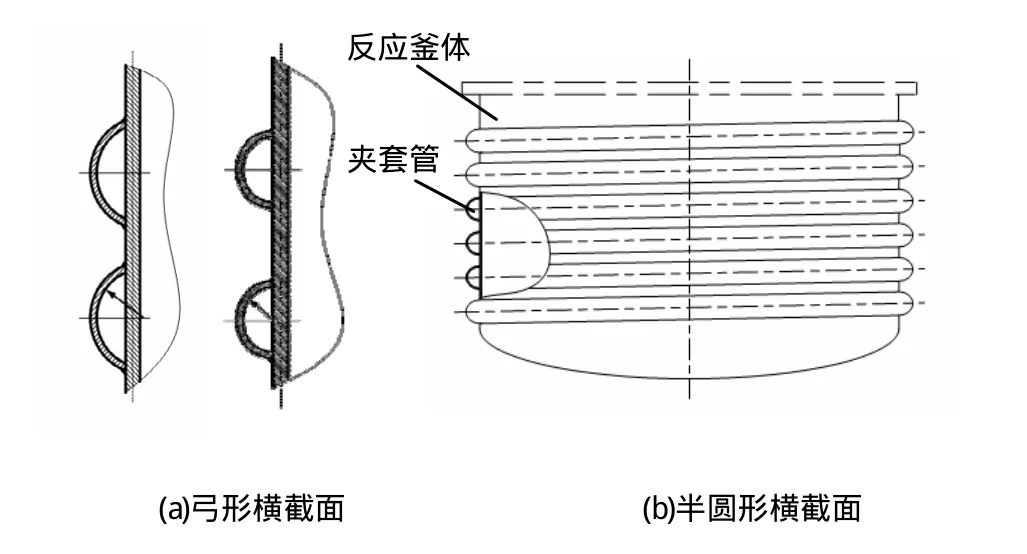
圖1 螺旋半管夾套的示意圖Fig.1 Schematic diagram of the half-pipe coiled jacket

李雅俠等[4,5]對釜外螺旋半圓管夾套內流體層流流動與換熱特性進行了數值模擬，給出了其內的流場與溫度場分布；文獻[6,7]對釜內、外螺旋半圓管夾套內流體充分發展的流動與換熱進行了對比，給出了充分發展層流狀態下的流動阻力和換熱系數的關聯式。

相對于橫截面為半圓形的螺旋半管夾套，在相同流量和換熱面積時，橫截面為弓形的螺旋半管夾套內的傳熱流體更容易獲得較高的流速并且具有節省材料的優點，因此研究其內流體流動及換熱特性具有重要工程實際意義，而目前相關的研究還沒有見到報道。本文采用數值方法對弓形截面螺旋半管夾套內流體湍流流動、換熱特性進行了研究，給出了正交螺旋坐標系下的流場和溫度場分布；研究了雷諾數Re、無量綱曲率δ對流動與換熱特性的影響；并將結果與橫截面為半圓形的螺旋半管夾套進行了對比，為工程實際中合理選擇和設計螺旋半管夾套提供了理論基礎。

1 物理模型

橫截面為弓形的螺旋半管夾套的物理模型可簡化為橫截面為弓形的螺旋通道，如圖2所示。

圖2 弓形截面螺旋半管夾套的物理模型Fig.2 Simplified physical model of half-pipe coiled jacket with arch cross section

其弓形面所在圓的中心角為120o。根據螺旋管道結構定義無量綱曲率δ和無量綱螺距τ為：

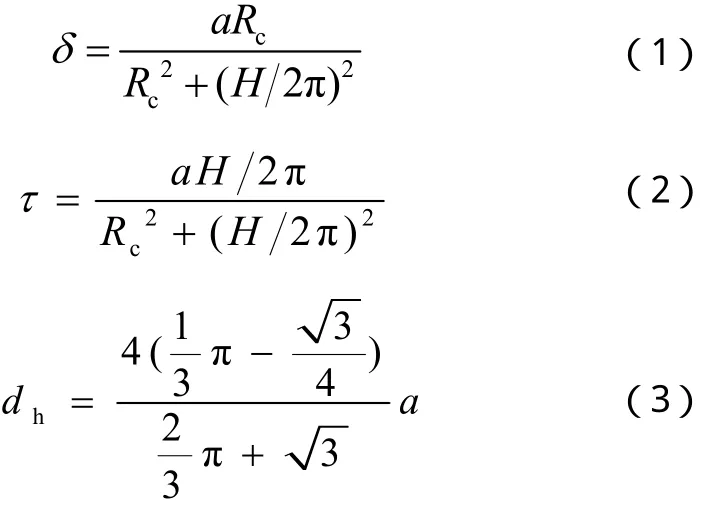
式中： dh—當量直徑；

a —弓形面所在圓的半徑；

H —螺距；

Rc—曲率半徑。

2 數值模擬

2.1 數值模擬方法

應用CFD分析軟件FLUENT，采用Realizable k-ε兩方程模型 ，基于柱坐標系對弓形截面螺旋半管夾套內流體的三維湍流流動與換熱進行了數值模擬。換熱邊界條件如圖2所示，即夾套管的外側彎曲壁面為絕熱壁面，內側直壁面為恒定高溫并設定Tw=393 K。以不可壓縮流體水為工作介質(密度ρ=998.2 kg/m3,動力粘度 μ=0.001 005 Pa?s)，采用均勻速度和溫度(T|θ=0=288 K)入口，出口采用充分發展出口的邊界條件；壁面采用無滑移壁面邊界條件，初始湍流強度按 Iinlet＝0.16Re-1/8估算。其中雷諾數Re 定義為：Re＝(ρvθmdh)/μ，vθm為截面平均速度，本文所研究的當量Re范圍在6 000～12 000之間。

2.2 計算網格

計算網格采用非結構六面體網格，網格節點間距為0.5 mm，橫截面上的網格如圖3所示。為了保證計算精度，進行了網格獨立性實驗，結果表明1 894 241個體積單元網格足可以滿足計算精度的要求。

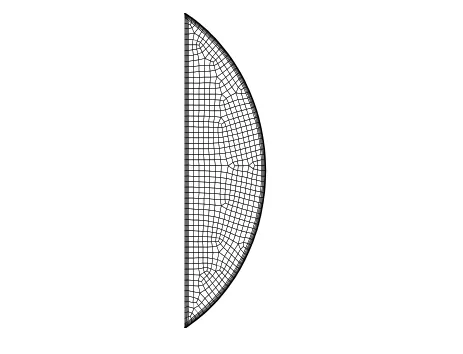
圖3 橫截面上網格分布Fig.3 Mesh of a cross section

2.3 數值計算結果的驗證

為了驗證模擬結果的準確性，采用相同的計算模型，以水為工作介質，計算了3圈的圓形截面螺旋管(Rc=200 mm， H=753.6 mm，圓管直徑d=20 mm)內的湍流流動及換熱，計算其充分發展段（θ=3π~5π之間）的阻力系數f和壁面平均努塞爾數Num，與文獻[9,10]給出的實驗關聯式(4)及(5)進行了對比，結果如圖4所示，其中f的最大誤差為6.67%，Num的最大誤差為7.97%，證明本文所采用的模型是可靠的。

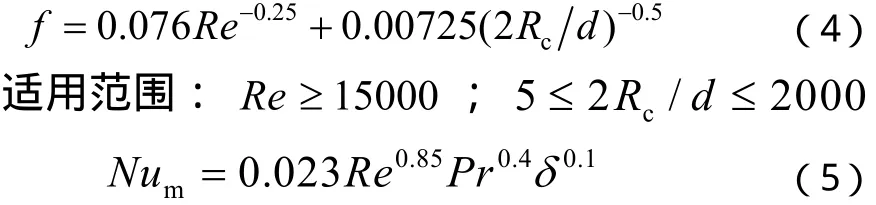
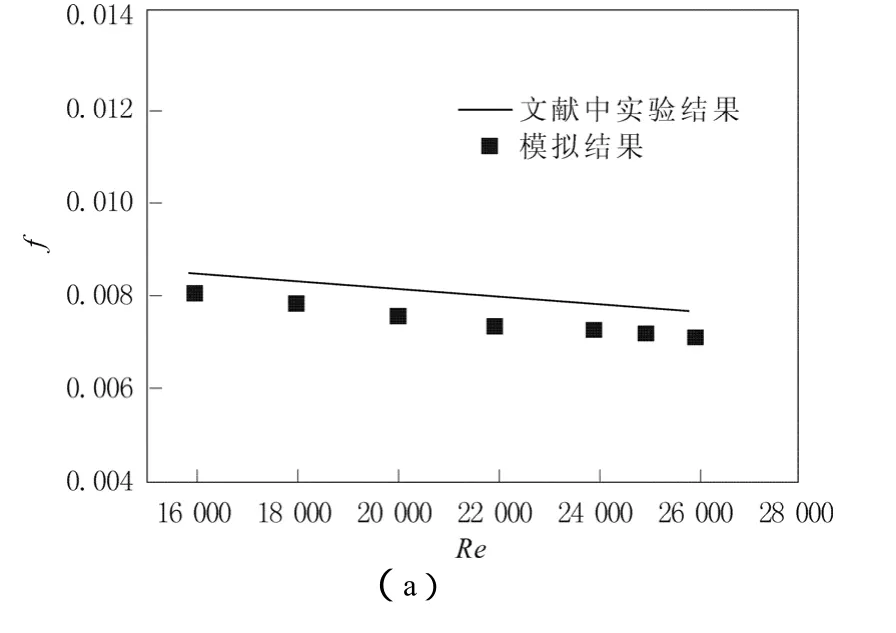
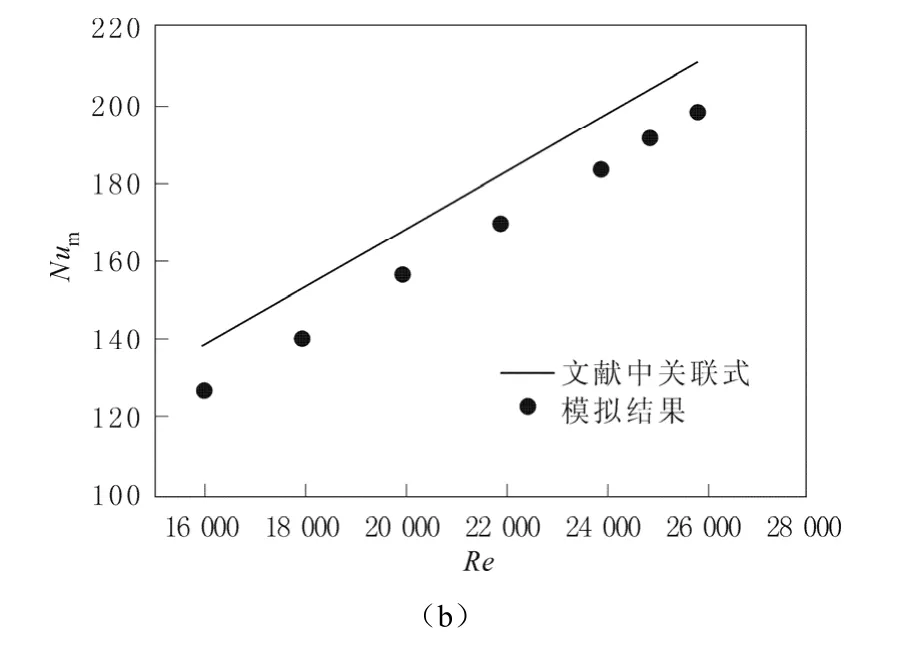
圖4 圓形截面螺旋管模擬結果與文獻結果對比Fig. 4 Comparison of numerical results and data reported in the literature for helical circular tube

2 結果與分析

文獻[11]中的研究結果表明，當反應釜的曲率半徑較大時，螺距對螺旋半管夾套內流體流動與換熱特性影響很小，因此本文主要研究了無量綱曲率 δ的影響。為了便于同半圓截面螺旋半管夾套進行對比并結合工程實際，本文對三種結構的弓形截面螺旋半管夾套(見表1)進行研究，每種結構的夾套均取為3圈。其中a1為半圓形截面夾套管的半徑，見圖5。

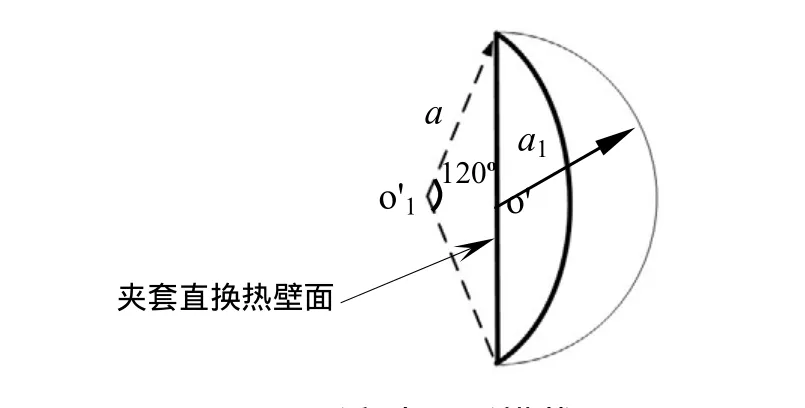
圖5 弓形和半圓形橫截面Fig. 5 Arch cross section and semicircular cross section

根據幾何結構可知：

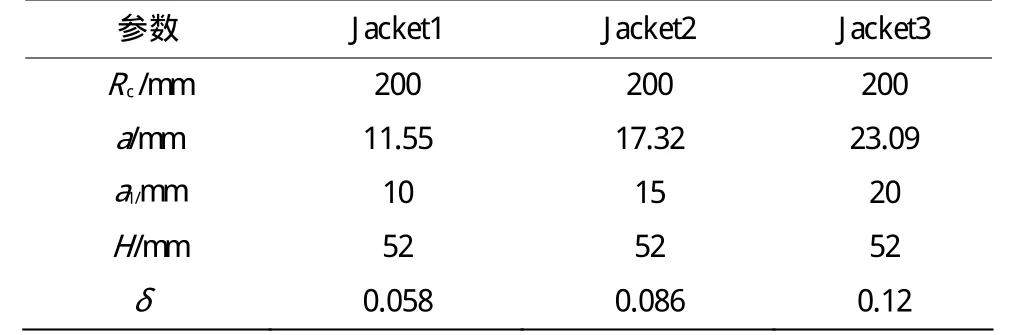
表1 夾套的結構參數Table 1 Structure parameters of jackets

3.1 流場

文獻[12]中指出流動和換熱充分發展時，無量綱速度和溫度與主流方向的位置無關，數值模擬結果表明，流體在本文所研究的夾套管內經過1.5圈后即θ≥3π后流場和溫度場均可達到充分發展。根據文獻[11]中給出的坐標變換方法，將數值模擬得到的柱坐標系下三維速度變換到正交螺旋坐標系x， y，s下(見圖2)，得到三維速度u，v，w。圖6中給出的即為 θ=5π的橫截面上的平均無量綱軸向速度w/wm、二次流速度及二次流函數 ψ的分布圖，wm為平均軸向速度。流函數定義為：

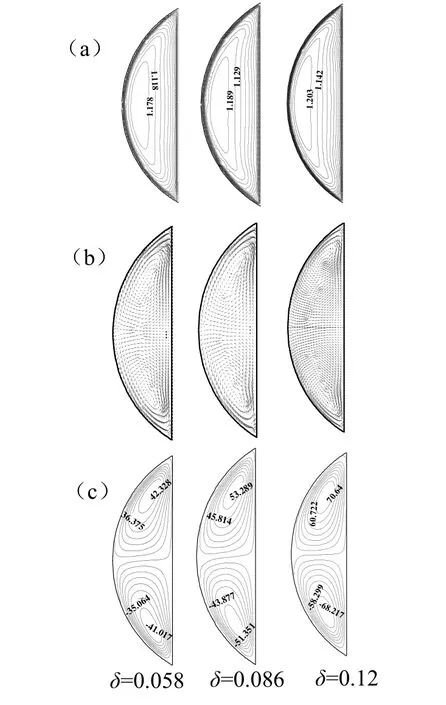
圖6 充分發展的流場分布(Re=10 000)Fig. 6 Fully developed flow fields(Re=10 000)

從圖中可以看出充分發展湍流時，在離心力的作用下，弓形截面螺旋半管夾套橫截面上軸向速度的最大值位置靠近彎曲的外壁側，二次流為旋轉方向相反的兩渦結構。同時可以看出隨著δ的增加，w/wm的最大值逐漸增大，這是由于流動阻力增大的緣故；同時δ增大，二次流函數值逐漸增大，主要是由于離心力增大，二次流強度增強。

3.2 溫度場

圖7中給出的是Re =10 000時，θ=5π的橫截面上無量綱溫度J的等值線，J定義為T為橫截面上各點溫度，Tw為換熱壁面溫度，Tm為截面平均溫度：Tm= òvθT d A ( vθmA)，其中A為換熱面積。從圖中可以看出，隨著δ的增加，橫截面上的溫度分布越來越均勻，說明換熱增強。同時還可以看出換熱壁面中心點附近的溫度梯度遠小于換熱壁面兩側的溫度梯度，這主要是由于二次流的作用，在二次流存在區域，換熱邊界層變薄，換熱增強；而中心點附近受二次流的影響較弱，換熱較差。

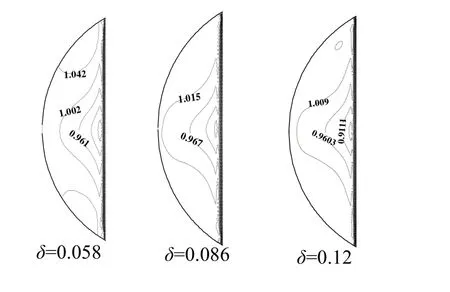
圖7 充分發展的溫度場(Re =10 000，θ=5π)Fig.7 Fully developed temperature fields

3.3 兩種螺旋半管夾套的對比

定義流動阻力系數f和換熱努塞爾數Nu為式（8）和（9）:

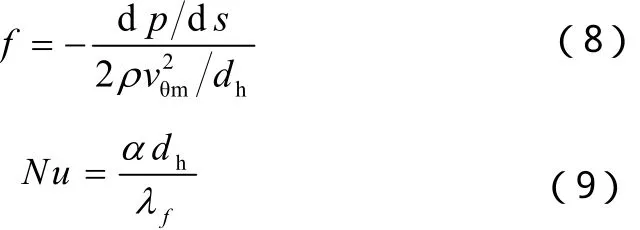
其中 dp/ds為湍流充分發展段(3π≤θ≤5π)，沿螺旋線單位長度的壓力降，α為對流換熱系數，λf為換熱流體的導熱系數。

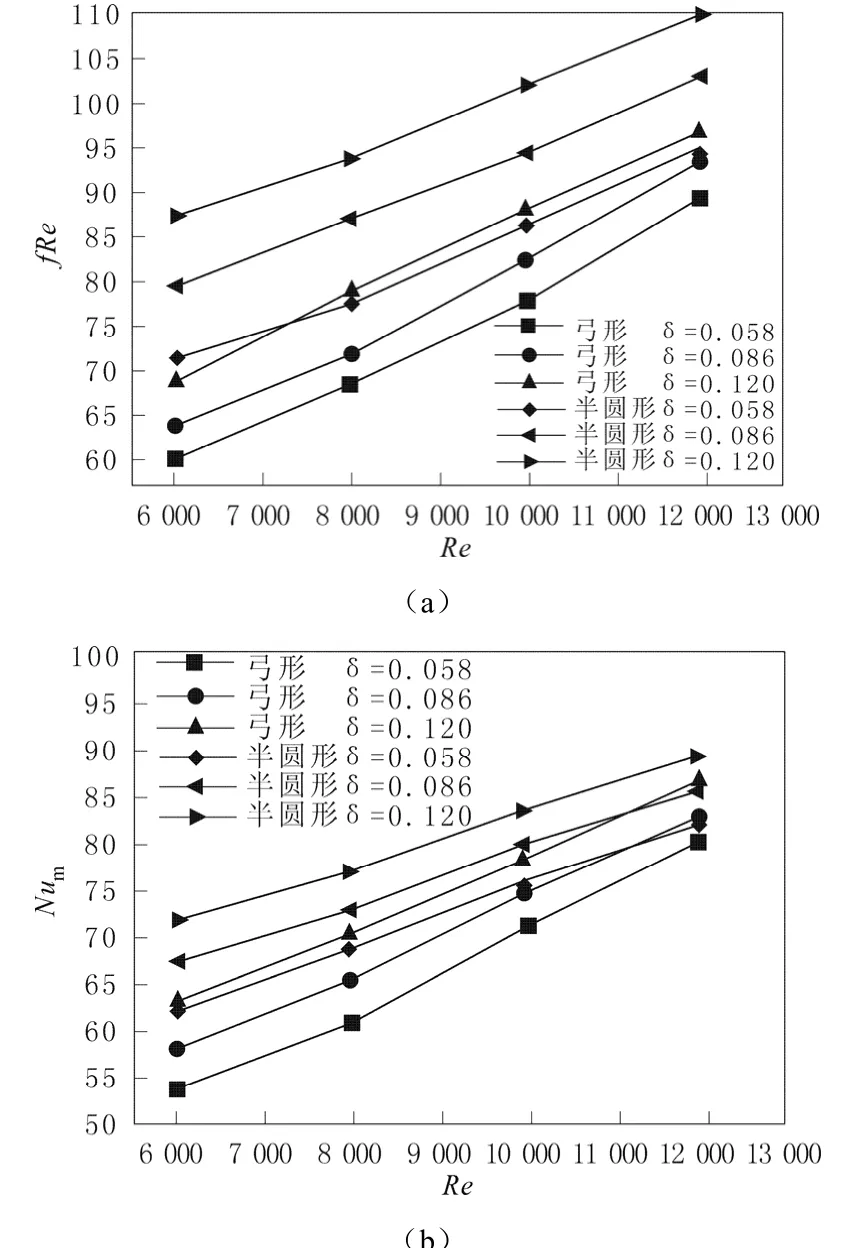
圖8 兩種螺旋半管夾套fRe和Num的對比Fig. 8 Comparison of fRe and Num of two types of half-pipe coiled jacket

圖8中給出的是弓形和半圓形截面螺旋半管夾套內湍流流動阻力fRe和換熱平均努塞爾數Num的對比。其中半圓形的半徑為a1(見表 1)，兩者的換熱面積相同(見圖5)。從圖8中可以看出隨著Re或δ的增加，兩種夾套的Num和fRe均增加。相同條件下，弓形截面夾套的Num小于半圓形截面夾套，同時其內的流動阻力也明顯小于半圓形截面夾套。計算結果表明，在 6 000≤Re≤12 000，0.058≤δ≤0.12 的范圍內，弓形截面夾套的平均努塞爾數 Num為半圓形截面夾套的0.86～0.98倍，而流動阻力fRe是其0.794~0.947倍，可見弓形截面夾套在減小流動阻力方面具有一定的優越性。另一方面，當換熱面積相同時，弓形截面螺旋半管夾套較半圓形截面半管夾套更加節省材料，因此在工程實際中有很大的應用價值。

4 結 論

(1) 流體在弓形截面螺旋半管夾套內作充分發展湍流流動時，軸向速度的最大值靠近彎曲的外壁側，橫截面上的二次流為旋轉方向相反的兩渦結構。

(2) 受二次流的影響，換熱面中心點附近的無量綱溫度梯度遠小于兩側的無量綱溫度梯度。

(3) 當內側直換熱壁面面積相同時，在0.058≤δ≤0.12，6 000≤Re≤12000的范圍內，弓形截面螺旋半管夾套的平均努塞爾數Num為半圓形截面螺旋半管夾套的 0.86～0.98倍，而流動阻力 fRe為其0.794~0.947倍。

［1］ 陳曉寧, 魏光亮, 杜念忠,等. 攪拌反應釜冷卻裝置—半管夾套的設計與制作[J].聚氯乙烯,2006(7):31-33.

［2］ Dhotre T., Murthy Z V P. Modeling and Dynamic Studies of Heat Transfer Cooling of Liquid in Half-Coil Jackets [J]. Chem. Eng. J.,2006,118(3): 183- 188.．

［3］ Jayakumar Natesan Subramanian，Farouq S. Mjalli. The Dynamics of Liquid Cooling in Half-Coil Jackets [J]. Chemical Product and Process Modeling, 2008, 3(1): 1-16.

［4］ 李雅俠, 王航, 吳劍華. 螺旋半圓管夾套內層流流動及換熱特性研究[J]. 化學工程, 2010,38(6):35-38.

［5］ 李雅俠，王航，吳劍華,等.螺旋半圓管夾套內充分發展層流流動與換熱特性[J].化工學報，2011，6(11): 2796-2803.

［6］ Yaxia Li, Jianhua Wu, Hongren Zhan. Fluid Flow and Heat Transfer Characteristic of Outer and Inner Half Coil Jackets[J]. Chinese J. Chem.Eng. , 2011, 19(2): 253-261.

［7］ Yaxia Li, Jianhua Wu, Li Zhang. Comparison of Fluid Flow and Heat Transfer Behavior in Outer and Inner Half Coil Jackets and Field Synergy Analysis[J]. Appl. Therm. Eng., 2011,31: 3078- 3083.

［8］ 王福軍.計算流體動力學分析—CFD軟件原理與應用[J].北京：清華大學出版社，2004:86-87.

［9］ Andrea Cioncolini, Lorenzo Santi. An Experimental Investigation Regarding the Laminar to Turbulent Flow Transition in Helically Coiled Pipes [J]. Exp. Therm. Fluid Sci., 2006, 30: 367–380.

［10］ Lin C X, EBADIANT M A. Developing Turbulent Convective Heat Transfer in Helical Pipes [J]. Int. J. Heat Mass Transfer, 1997, 40(16):3861-3873.

［11］ 李雅俠, 吳劍華, 龔斌. 螺旋半圓管夾套內湍流流動與傳熱的數值模擬[J]. 過程工程學報, 2010,10(4): 644-649.

［12］ 陶文銓．數值傳熱學 [M]. 第2版.西安交通大學出版社, 2008-01:109-111.