基于K-Medoids聚類的多傳感器航跡關(guān)聯(lián)算法

徐 麗，馬培軍，蘇小紅

(1.哈爾濱工業(yè)大學計算機科學與技術(shù)學院，150001哈爾濱，xuli－h(huán)it@126.com;2.哈爾濱工程大學計算機科學與技術(shù)學院，150001哈爾濱)

航跡融合必須以航跡關(guān)聯(lián)為前提，因此關(guān)聯(lián)判定的準確性將直接影響到整個航跡融合系統(tǒng)的性能.航跡關(guān)聯(lián)備受國內(nèi)外學者關(guān)注，一直是研究的熱點問題之一.Ashraf M.Aziz[1]提出了一種基于模糊均值聚類的航跡融合方法來解決分布式多傳感器多目標多屬性重疊覆蓋場景中的航跡關(guān)聯(lián)和融合問題.Baoguo Tian等[2]將航跡關(guān)聯(lián)問題轉(zhuǎn)化成多維分配問題進行求解.Songhwai Oh等[3]用馬爾科夫鏈蒙特卡洛數(shù)據(jù)關(guān)聯(lián)算法較好地解決了目標密集環(huán)境下的航跡關(guān)聯(lián)問題.Huang Youpeng等[4]提出了一種基于灰色關(guān)聯(lián)分析的航跡關(guān)聯(lián)算法，有效地實現(xiàn)了異構(gòu)傳感器的航跡關(guān)聯(lián).Kusha Panta等[5]提出了混合高斯概率假設(shè)密度濾波的航跡關(guān)聯(lián).Mei Duan等[6]提出了基于神經(jīng)網(wǎng)絡(luò)的航跡關(guān)聯(lián)算法.這些算法的提出提高了多傳感器航跡融合系統(tǒng)的效率.近年來，還有很多學者從其他角度研究了航跡關(guān)聯(lián)問題.Donald E.Maurer[7]對關(guān)聯(lián)的信息進行處理，提高了整個系統(tǒng)的效率.Lance M.Kaplan等[8]提出了關(guān)聯(lián)多條航跡的代價函數(shù).Dimitri J.Papageorgiou 等[9]擴展了最佳偏差關(guān)聯(lián)假設(shè)和相應(yīng)的偏差關(guān)聯(lián)似然函數(shù)，使其更適合系統(tǒng)級航跡歧義管理.這些成果很大程度上促進了航跡關(guān)聯(lián)問題的研究.特別是，文獻[10]根據(jù)數(shù)據(jù)列因素之間發(fā)展態(tài)勢的相似或相異程度來衡量航跡間接近的程度，首次用模式識別的方法解決了航跡關(guān)聯(lián)問題，為求解航跡關(guān)聯(lián)問題探索了一條新的途徑.

本文提出了一種新的基于K-Medoids聚類的航跡關(guān)聯(lián)算法.該算法采用局部航跡與系統(tǒng)航跡關(guān)聯(lián)的策略，大大降低了需要關(guān)聯(lián)的航跡對數(shù)量，從而提高了關(guān)聯(lián)算法的效率.

1 系統(tǒng)描述

假設(shè)M個傳感器觀測雜波中的T個目標，在固定時間間隔內(nèi)獲取觀測，每個觀測都由幾個量測組成，共觀測n步.

設(shè)Xi(k)(1≤i≤T)為第k個測量時刻目標i的狀態(tài)向量，假設(shè)輸入項為零，則目標運動模型為

式中:Xi(k+1)為k+1時刻目標i的狀態(tài)向量;F(k)為狀態(tài)轉(zhuǎn)移矩陣;G(k)為輸入控制矩陣;ui(k)為加速度輸入矩陣;vi(k)為離散時間白噪聲序列，滿足

測量方程可表示為

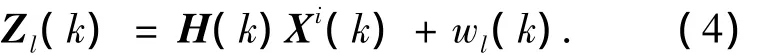
式中:wl(k)為零均值，方差為Rl(k)的Gauss觀測噪聲;H(k)是觀測矩陣.

2 基于K-Medoids聚類的航跡關(guān)聯(lián)算法

在分布式結(jié)構(gòu)的航跡融合系統(tǒng)中，每個傳感器都獨立地處理它的局部量測，產(chǎn)生局部航跡并送至融合中心，融合中心根據(jù)各傳感器的航跡數(shù)據(jù)完成航跡關(guān)聯(lián)和航跡狀態(tài)估計融合，形成全局估計.航跡關(guān)聯(lián)的工作就是將來自不同傳感器的航跡進行分組，使得同一組的航跡代表同一個目標.而聚類是將要處理的對象分成若干個類，使得同一類的對象盡量相似，不同類的對象盡量相異.二者都可用于發(fā)現(xiàn)隱藏在數(shù)據(jù)背后的分組和數(shù)據(jù)分布信息.實際上，二者的目標和作用是一致的.通過上述分析，可以從一個新的角度重新理解航跡關(guān)聯(lián)問題.

2.1 關(guān)聯(lián)策略

K-Medoids聚類算法屬于劃分方法中的一種常用的聚類算法，具有較高的準確性.因為Medoids不容易被極端數(shù)據(jù)影響，當存在噪聲和孤立點數(shù)據(jù)時，K-Medoids算法依然很健壯，適合數(shù)據(jù)比較密集的數(shù)據(jù)集.然而，K-Medoids算法也存在一些缺陷:1)初始化敏感;2)聚類結(jié)果多樣化;3)在進行Medoids輪換時需遍歷所有非Medoids，執(zhí)行代價較高.

由于在分布式多傳感器航跡融合系統(tǒng)的實際應(yīng)用中，所使用的傳感器和每個傳感器所掃描的目標數(shù)量都很多，如果對所有來自不同傳感器的航跡都進行兩兩關(guān)聯(lián)及融合處理，那將會給系統(tǒng)帶來沉重的負擔.因此，本文采用將局部航跡與系統(tǒng)航跡進行關(guān)聯(lián)的策略，指定每條系統(tǒng)航跡作為一個固定的Mediod，這樣就避免了K-Medoids算法初始化的隨機性，也避免了Medoids輪換的沉重代價.而這種策略，本身就大大降低了需要關(guān)聯(lián)的航跡對數(shù)量，使系統(tǒng)的效率得到了很大程度的提高.另外，由于來自同一傳感器的航跡都是由不同目標形成的，所以一條系統(tǒng)航跡最多只能與來自某個傳感器的一條局部航跡關(guān)聯(lián)成功;又由于每條系統(tǒng)航跡都源于不同的目標，所以來自一個傳感器的某條局部航跡最多只能與一條系統(tǒng)航跡關(guān)聯(lián)成功，因此算法將根據(jù)規(guī)則最多為一條局部航跡找到一條系統(tǒng)航跡與其關(guān)聯(lián)，這樣避免了聚類結(jié)果的多樣性.

2.2 算法描述

Step1 確定Mediods.

設(shè)系統(tǒng)航跡和來自傳感器l的局部航跡的航跡號集合分別為

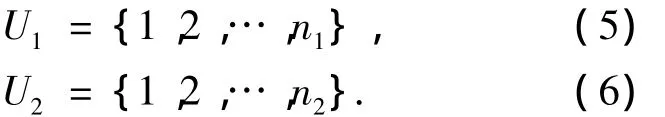
即系統(tǒng)航跡集合中有n1條系統(tǒng)航跡，來自傳感器l的局部航跡集合中有n2條局部航跡.

指定每條系統(tǒng)航跡作為一個Mediod，每個Medoid標識一個類，共n1個類.記為

傳感器l的n2條局部航跡記為

Step2 計算兩條航跡k時刻點跡的距離.

假設(shè)航跡i在k時刻經(jīng)過標準化處理后的狀態(tài)向量為

相應(yīng)的分辨率為

式中:rk為航跡的特征;n為特征的個數(shù);δk為每個特征相對應(yīng)的分辨率.

利用無窮范數(shù)定義航跡i和航跡j在k時刻的點跡距離為

進而，利用平均值法計算出描述兩條航跡接近程度的近似距離，即

Step 3 構(gòu)造來自傳感器l的局部航跡與Medoids的距離矩陣.

當計算出兩條航跡的近似距離之后，可以構(gòu)造出來自傳感器l的局部航跡與Medoids的距離矩陣為

Step 4 關(guān)聯(lián)準則.

根據(jù)與Medoids距離最近的原則，即 di=且di＜dii.將待關(guān)聯(lián)的局部航跡分到各個類中去，即指派每個局部航跡給離它最近的Medoid所代表的類.當一個Medoid與多條局部航跡距離相等且都為最小時，由于一條系統(tǒng)航跡最多只能與來自某個傳感器的一條局部航跡來自同一個目標，且目標位置是關(guān)聯(lián)判決中一個較為關(guān)鍵的屬性，算法將選擇與該Medoid平均位置無窮范數(shù)最小的局部航跡作為最終的關(guān)聯(lián)航跡.當di＞dii時，說明該局部航跡不與任何Medoids關(guān)聯(lián)，這時指定此局部航跡作為一個新的Medoid.這樣就給出了系統(tǒng)航跡與來自傳感器l的局部航跡的關(guān)聯(lián)判決.

Step 5 多義性處理.

一條來自某個傳感器的局部航跡最多只能與一條系統(tǒng)航跡關(guān)聯(lián).因此當一條局部航跡與多條系統(tǒng)航跡關(guān)聯(lián)成功時，需要進行多義性處理.在這種情況下算法選擇與該局部航跡距離最小的系統(tǒng)航跡為關(guān)聯(lián)航跡，如果與該局部航跡距離最小的系統(tǒng)航跡依舊有多條，則算法選取其中平均位置無窮范數(shù)最小的那條系統(tǒng)航跡作為最終與該局部航跡關(guān)聯(lián)的航跡.經(jīng)過多義性處理后，每條局部航跡就最多只能與一條系統(tǒng)航跡關(guān)聯(lián)成功.

經(jīng)航跡關(guān)聯(lián)后，將關(guān)聯(lián)成功的航跡對進行航跡狀態(tài)估計融合.

3 實驗分析

3.1 初始設(shè)置

為了討論問題方便，假設(shè)送至融合中心的所有狀態(tài)估計都在相同的坐標系里，并且各傳感器同步采樣，數(shù)據(jù)的傳輸延遲時間為0.仿真實驗采用兩個傳感器同時觀測目標，模擬目標在三維空間中做變速機動運動.為了驗證算法的性能，采用Monte Carlo方法對本文算法進行50次仿真.仿真考慮兩種情況:1)模擬中等密度目標環(huán)境，開始進入公共區(qū)的目標為60批;2)模擬密集目標環(huán)境，開始進入公共區(qū)的目標為120批.圖1和圖2分別給出了在公共觀測區(qū)域60批目標和120批目標的運動軌跡.

圖1 60批目標航跡圖

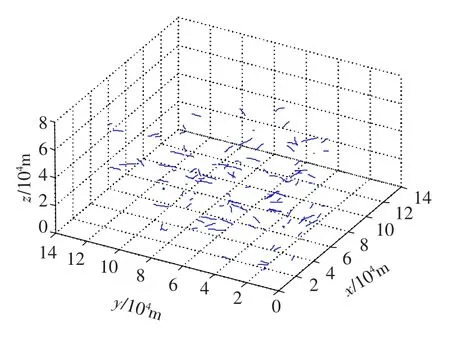
圖2 120批目標航跡圖

3.2 實驗結(jié)果與分析

圖3與圖4分別給出了在60批目標下分別采用最近鄰域法(NN)、模糊C均值法(FCM)及本文算法(K-Mediods)，仿真50次后的平均正確關(guān)聯(lián)率(Pc)曲線和平均錯誤關(guān)聯(lián)率(Pe)曲線.

圖5與圖6分別給出了在120批目標下分別采用最近鄰域法(NN)、模糊C均值法(FCM)及本文算法(K-Mediods)，仿真50次后的平均正確關(guān)聯(lián)率(Pc)曲線和平均錯誤關(guān)聯(lián)率(Pe)曲線.

圖3 60批目標下正確關(guān)聯(lián)率對比

圖4 60批目標下錯誤關(guān)聯(lián)率對比

圖5 120批目標下正確關(guān)聯(lián)率對比

圖6 120批目標下錯誤關(guān)聯(lián)率對比

表1統(tǒng)計了采用最近鄰域法(NN)、模糊C均值(FCM)及本文算法(K-Mediods)對各目標進行航跡關(guān)聯(lián)的平均計算時間.

表1 關(guān)聯(lián)時間對比 s

從實驗結(jié)果可以看出最近鄰域法速度很快，但是正確關(guān)聯(lián)率最低.該算法不適合中等密度和密集目標環(huán)境，特別在密集目標環(huán)境下，隨著關(guān)聯(lián)時間步的增加，其正確關(guān)聯(lián)率逐步下降.模糊C均值法的正確關(guān)聯(lián)率較高，在中等密度目標環(huán)境下與K-Mediods方法相當，但在密集目標環(huán)境下，其正確關(guān)聯(lián)率與K-Mediods方法的差距變大，且效率較低.本文算法K-Mediods方法的正確關(guān)聯(lián)率在中等密度和密集目標環(huán)境下都為最高，在目標密集環(huán)境下，仍然可以達到較高的正確關(guān)聯(lián)率.

4 結(jié)論

1)基于K-Medoids聚類的航跡關(guān)聯(lián)算法采用局部航跡與系統(tǒng)航跡關(guān)聯(lián)的策略，減少了需要關(guān)聯(lián)的航跡對數(shù)量，縮短了關(guān)聯(lián)時間，提高了系統(tǒng)的效率;系統(tǒng)航跡被指定為 Mediods，使得用K-Mediods聚類方法求解航跡關(guān)聯(lián)問題克服了該方法本身的缺陷.

2)通過用無窮范數(shù)量化兩條航跡在采樣點的點跡距離得到了兩條航跡的近似距離，從而確定了來自某個傳感器的局部航跡與系統(tǒng)航跡的關(guān)聯(lián)矩陣，使得關(guān)聯(lián)判決能考慮當前和歷史航跡，提高了正確關(guān)聯(lián)率.

3)模擬實驗表明該算法在目標密集環(huán)境下，以較小的計算開銷達到了較高的精度.由于K-Medoids聚類算法本身的優(yōu)越性，算法在存在噪聲和離群點時，具有很強的健壯性.

[1]AZIZ A M.Fuzzy track-to-track association and track fusion approach in distributed multisensor—multitarget multiple-attribute environment[J].Signal Processing，2007，87(6):1474－1492.

[2]TIAN B G，ZHANG J P，YANG S L.Algorithm of fuzzy track correlation in multisensor system based on neural network[C]//Proceedings of the 8th International Conference on Signal Processing.Washington，DC:IEEE Computer Society，2006:316－319.

[3]OH S，RUSSELL S，SHANKAR S.Markov chain Monte Carlo data association for multi-target tracking[J].IEEE Transactions on Automatic Control， 2009，54(3):481－497.

[4]HUANG Y P，ZHOU Y F，ZHANG H B.Heterogeneous sensors track-to-track correlation algorithm based on gray correlative degree[C]//Proceedings of the 2008 International Symposium on Computer Science and Computational Technology.Washington，DC:IEEE Computer Society，2008:104－108.

[5]PANTA K，CLARK D E，VO B.Data ASsociation and track management for the gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Aerospace and Electronic Systems，2009，45(3):1003 －1016.

[6]DUAN M，LIU J H.Track correlation algorithm based on neural network[C]//Proceedings of the 2009 Second International Symposium on Computational Intelligence and Design.Washington，DC:IEEE Computer Society，2009:181－185.

[7]MAURER D E.Information handover for track-to-track correlation[J].Information Fusion，2003，4(4):281 －295.

[8]KAPLAN L M，BAR-SHALOM Y，BLAIR W D.Assignment costs for multiple sensor track-to-track association[J].IEEE Transactions on Aerospace and Electronic Systems，2008，44(2):655－677.

[9]PAPAGEORGIOU D J，HOLENDER M.Track-to-track association and ambiguity management in the presence of sensor bias[C]//Proceedings of the 12th International Conference on Information Fusion.Washington，DC:IEEE Computer Society，2009:2012 －2019.

[10]衣曉，關(guān)欣，何友.分布式多目標跟蹤系統(tǒng)的灰色航跡關(guān)聯(lián)模型[J].信號處理，2005，21(6):653－655，662.