連續小推力航天器軌道交會問題的制導律設計

張萬里，王常虹，夏紅偉，解偉男

(1.哈爾濱工業大學空間控制與慣性技術研究中心，150001哈爾濱，zhangwanli1983@gmail.com;2.中國空空導彈研究院，471009河南 洛陽)

近年來交會對接技術一直是研究的重點之一[1]，而空間交會的制導律設計是完成交會任務的關鍵，目前近距離交會制導律的設計一般為脈沖推力的假設情況下的多脈沖機動，如Hari B.H[2]提出的使航天器相對速度隨著距離指數下降，從而保證交會安全的制導方法，Lopez[3]提出勢函數制導法，將目標點處勢能設置為最小，而初始位置和障礙處的勢能設置為較大值，通過使航天器沿著勢能減小方向運動從而使其向目標靠近并實現避障機動.梁立波[4]提出的斜滑制導算法，采用對數函數映射法進行脈沖尋優，實現燃料最省交會.但因實際交會時脈沖推力假設一般無法滿足，航天器的速度改變需要一定的時間，此時必然存在推力弧段與自由飛行弧段，當考慮此因素后實際交會軌跡與名義軌跡偏差較大，針對如何對實際軌跡進行閉環校正使其終止位置與名義軌跡重合，陳偉躍[5]設計了小推力速度閉環交會制導律，通過對若干制導周期內的速度脈沖求取實現軌跡校正，但其實現需要若干不定的制導周期，且在每個周期內需重新求取速度脈沖，計算量復雜.

隨著高比沖小推力推進系統的日益成熟，采用小推力推進器實現軌道交會可以避免脈沖假設帶來的軌跡偏差，且通過設計軌道各個方向的控制變量變化，可以實現燃料最優交會.本文使用高比沖小推力推進系統為執行機構，設計空間交會問題的燃料最優時間連續制導律.首先給出軌道交會問題的數學模型，并給出最優控制問題的目標函數和約束條件，然后利用直接法將控制變量離散化，通過參數尋優得到對應燃料最優的控制變量參數和交會時間常數，從而求得最優交會軌跡.

微分代數(differential algebraic，DA)是由Martin Berz[6]建立的利用代數方法求解解析問題的有效手段.P.D.Lizia[7]將此應用在對星際間連續小推力的軌道轉移的修正上，R.Armellin[8]將其用于行星引力輔助軌道轉移問題.本文將該方法應用于軌道交會情形.因在軌道交會推進系統的實際點火時刻與名義點火時刻常常存在一定量的偏差，從而導致實際交會軌跡與名義交會軌跡同樣會存在偏差.本文針對此情況，首先給出利用微分代數方法實現常微分方程積分的途徑，并對初值擾動情形下，微分代數變量階數不同對于積分軌跡的影響情況進行分析，最后利用微分代數工具求取小推力情況下點火時刻偏差對應的部分控制變量修正值，從而完成軌跡修正.

1 求解航天器交會燃料最優控制問題

1.1 航天器交會相對動力學方程

在交會的最終逼近階段，可以由Clohessy-Wiltshire(C-W)方程來近似描述2個飛行器的相對運動狀態.該方程建立在目標航天器的當地垂直當地水平(local-vertical-local-horizontal，LVLH)坐標系下，坐標系各軸具體方向如圖1所示.

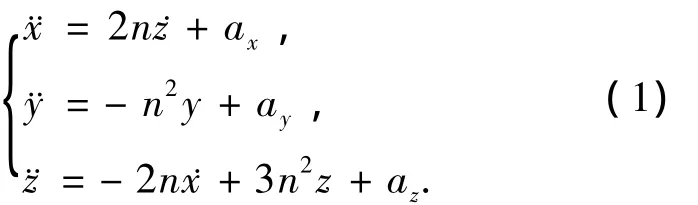
在LVLH坐標系下得到的線性化后簡化C-W方程，具體形式為其中:ax、ay、az表示在LVLH坐標系中施加于追蹤航天器上的3個方向的加速度，n為目標航天器的軌道角速度.本文通過對控制變量ax、ay、az的設計，使航天器軌道交會過程燃料實現最優，并求出對應的最優軌跡.

圖1 當地垂直當地水平坐標系

1.2 利用直接法求解燃料最優交會問題

對于航天器在連續推力下的燃料最優軌跡優化問題，目前常用的數值方法包括間接法和直接法.間接法通過對原始問題的一階最優必要條件進行離散化，求解滿足此條件的方程，從而得到滿足原始最優控制問題的解.但此法求解繁瑣，收斂域小，對于各種變量尤其是無實際物理意義的協態變量初值猜測難度高.直接法通過將控制變量離散化，避開最優必要條件的求解步驟，通過將離散節點處的控制變量值設置為尋優參數，后利用尋優函數求取此最優控制問題.直接法相比而言具有收斂域大、求解簡單、無需對協態變量進行初值猜測等優點，因此其實用性較強，也是當前求解此類問題的主流方法.本文利用直接法求取燃料最優的最優控制問題，下面具體說明其在軌道交會問題上的實現方式.

1)確定交會過程中間停靠點.基于文獻[2]中提出的使航天器相對速度隨著距離指數下降的制導方法，本文按照以下方式確定交會過程中保持點的位置和速度:假設初始交會位置與目標位置距離為r0，則若干個位置保持點與目標位置成比例k1下降，即越靠近目標，轉移軌跡范圍越小，同時使速度幅值成比例k2下降，保證航天器交會過程中速度越來越小.在將交會過程分段完畢后，對每段獨立求解燃料最優問題，同時每段的初始時刻的位置、速度和終止時刻的位置、速度已給定.

2)離散化控制變量.首先要進行離散化控制變量，通過將每一階段軌道交會時間三等分得到包括初始時刻和終端時刻在內的4個時間節點，分別設置為 T0、T1、T2、T3.將每個時間節點處的控制變量設置為尋優參數 Ux0、Uy0、Uz0、…、Ux3、Uy3、Uz3，因軌道交會涉及 x、y、z 3 個方向，因此得到12個控制變量參數.同時因軌道交會時間未定，將軌道交會所需時間Ttrans設置為獨立參數，共記13個參數.

3)建立必要的約束條件.由于每個階段軌道交會的終止位置和速度都已給定，對于終端位置和速度存在共6個約束條件，即

式(2)中的航天器終端狀態 RT、VT通過對C-W方程進行積分求得，積分中的連續變量ax、ay、az通過對控制變量參數 Ux0、Uy0、Uz0、…、Ux3、Uy3、Uz3進行Lagrange插值獲得，交會時間Ttrans同樣為待優化參數.

4)確定所需目標函數.本文需要求取燃料最省軌道交會問題，因此其目標函數可設置為

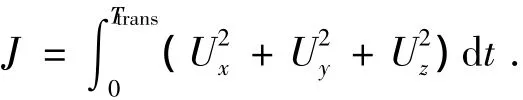
其中Ux、Uy、Uz同樣通過對控制變量參數進行Lagrange插值獲得.

5)參數尋優.通過以上步驟定義了軌道交會燃料最少最優控制問題所需的離散化尋優參數，各種約束條件以及最優控制的目標函數，利用Fmincon函數即可完成尋優過程.通過對12個控制變量參數進行Lagrange插值即可得到在各個階段軌道交會問題所需的連續控制變量ax、ay、az.

2 利用DA求解存在點火誤差時控制變量修正值

上節利用直接法求出了燃料最省的名義最優交會軌跡，但在實際完成軌道轉移的過程中，航天器的初始狀態常常存在擾動情況，本文就以實際點火時刻與給定時刻存在偏差為例，利用微分代數方法求解關于部分控制變量的修正問題.首先對于利用DA工具實現常微分方程積分的途徑進行簡要說明，并給出其針對初值擾動進行靈敏度分析的辦法.然后針對點火時刻偏差情形，利用微分代數工具給出求解控制變量修正值的具體步驟.

2.1 利用微分代數工具積分常微分方程

微分代數是由Martin Berz在上世紀八十年代末發展起來的利用代數方法求解解析問題的一種有效的手段，利用微分代數工具，可以求取多元函數關于變量的任意階泰勒展開，并根據對其泰勒展開系數的各種操作，實現對原函數的復合運算、求逆運算、積分常微分方程、求解兩點邊值問題(two point boundary value problem，TPBVP)、進行參數靈敏度分析等.本文利用COSY Infinity軟件實現以上操作，其中包含了DA數據類型的定義及一些基本的函數操作方法，可以方便的利用微分代數解決實際問題.因求解軌道交會問題需進行積分操作，下面針對DA實現常微分方程積分以及對初值擾動的靈敏度分析，簡單介紹DA的使用方法.

利用計算機實現任何數值積分操作，都是通過求取在若干積分點處的函數值后對其進行代數操作完成的，以一維初值問題為例:

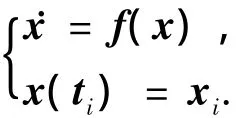
考察對式(2)實現的第一步歐拉前向積分，即

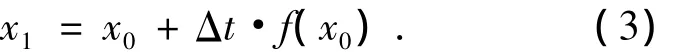
對于目前常規的數值積分程序，將其中x0=xi取為變量初值時，即可求取經過Δt時間間隔后的變量取值x1.但在微分代數框架內實現此過程，需將初值xi設置為變量初值與DA變量da相加的形式，即

通過將此數值積分過程在DA框架內繼續，即可得出在積分結束時刻tf處變量x關于初值的taylor展開值.即

利用式(4)，選擇不同的初始值擾動daxi，即可通過簡單的多項式代入操作求取積分終止時刻變量xtf的取值，而不必對每一個實際初始值重新進行數值積分操作，因此可非常方便的實現對于初值的靈敏度分析操作.而當DA變量選取的階數不同時，利用DA工具求取的xtf的準確性也有所不同，這將在后面的仿真分析中具體說明.

2.2 存在點火時刻偏差時利用DA求解制導律的修正值

利用微分代數方法，可方便的在存在點火時刻誤差情況下，求取相應的節點處控制變量的修正情況，而不必針對每種實際情況重新求解最優控制問題，具體求解步驟如下.

1)首先定義一點火時刻滯后偏差DA變量da(1)，從而求得航天器軌道交會所需時間為

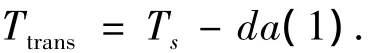
其中Ts分別是上節求出的名義軌道交會時間.在實際點火時刻之前，航天器在無推力情形下，即式(1)中 ax、ay、az=0 條件下運動，運動時間為da(1).

2)針對上述最優控制問題離散化的4個節點以及12個控制變量而言，本文假定存在點火時刻偏差情況下，對于初始時刻節點和終止時刻節點處的控制變量進行修正，因此可定義6個DA變量da(2)～da(7)，分別對應T0和T3時刻3個方向的控制變量修正值.

3)首先通過對動力學方程(1)在ax、ay、az=0條件下積分da(1)時間，從而求取實際的初始點火時刻時航天器對應的位置和速度值.然后，對動力學方程(1)積分Ttrans時間，求取終端位置和速度值.由于此時積分時間da(1)和Ttrans中包含待定DA變量，可將原始動力學方程轉化為

這樣只需進行[0，1]時間間隔內的積分操作，即可完成方程ODE積分過程，從而避免了在積分時間內存在DA變量的問題.

4)此時對常微分方程積分可求得對應于終止時刻的位置和速度關于初始位置和初始速度的函數關系式，通過簡單的多項式代入即可求得

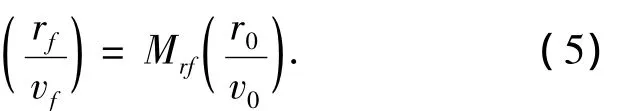
而此時的r0、v0都只與點火時刻Tini有關.

將式(5)兩邊的名義初始位置、初始速度和終止位置、終止速度減去，則可得如下的對應于位置速度偏差的關系式:

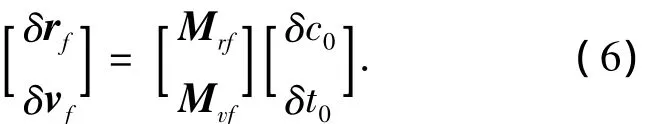
其中 δc0為 6維控制變量修正向量，因此[δc0δt0]T為7維向量.為使得關于DA的求逆運算成為可能，在方程(6)的左邊增廣一行δt0，得到如下關系式:

妹妹將父母在小城最后一套房子賣掉——這次回去，基本上算無家可歸了，暫借于妹妹同學家。小區臨江，大約是過去三號碼頭的位置。無論清晨，抑或日暮，站在陽臺，可聞江水氣息。

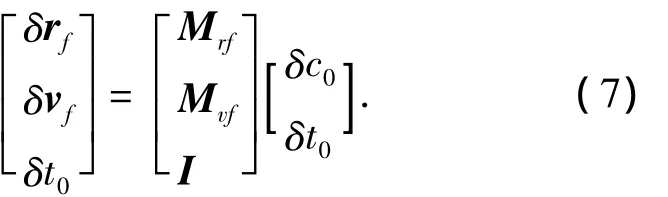
5)式(7)中[MrfMvfI]T為7維方陣，進行求逆運算，利用COSY軟件中關于DA變量的求逆算子MI，即可完成求逆操作，如下:

因為對于軌道交會問題，要求終止時刻的航天器位置向量和速度向量與名義位置向量和名義速度向量相同，因此可將上式中的δrf和δvf設置為零.即可求得針對于點火時刻偏差δt0所需的控制變量校正值δc0，將此校正值與名義控制變量相加，即可得到時間節點T0和T3時刻的新的控制變量值.

3 仿真分析

針對上節內容進行仿真驗證，首先給出利用直接法求取的航天器交會燃料最優軌跡以及航天器速度、質量和控制變量隨時間的變化關系.然后給出利用微分代數方法實現常微分方程積分的具體仿真結果.當初值存在一定量擾動，且選取DA變量階數不同時，給出利用DA工具所得的初值擾動靈敏度分析結果與真實數值積分結果的關系.最后給出在初始點火時刻與名義點火時刻存在偏差情形下，利用微分代數方法求取的控制變量修正值以及航天器的修正軌跡.

3.1 直接法求取的最優軌跡

按照1.2節方法，利用直接法通過對其尋優得到在滿足各種約束條件情況下，目標函數最小的14個參數變量，將參數變量中的控制變量關于時間進行Lagrange插值，即可求得所需的控制推力函數.仿真中所選目標航天器初始軌道參數如表1所示.

表1 航天器初始軌道參數

追蹤航天器質量為1 000 kg，小推力發動機比沖為3 000 s.按照1.2節求取中間位置保持點，取k1=5，k2=10.即位置以5倍減少速度向交會點靠近，速度以10倍減少速度降低.可得到追蹤飛行器在目標飛行器LVLH坐標系中的初始位置、速度和保持點位置、速度如表2所示.

表2 航天器位置速度參數

圖2～圖5分別給出了求解的追蹤航天器的x、z向位置名義最優軌跡，速度、控制變量和質量隨時間的變化關系.利用直接法求取的每個階段的交會時間分別為 146.42、191.86和 157.58 s，圖2中小圖分別給出了追蹤航天器在交會保持點的軌跡細節圖，從圖中可見，追蹤航天器可以在交會保持點滿足指定位置和速度要求.推進發動機各個方向的推力隨時間由大變小，至1E－4數量級.航天器質量從初始的1 000 kg減少至973.4 kg，共消耗燃料26.6 kg.

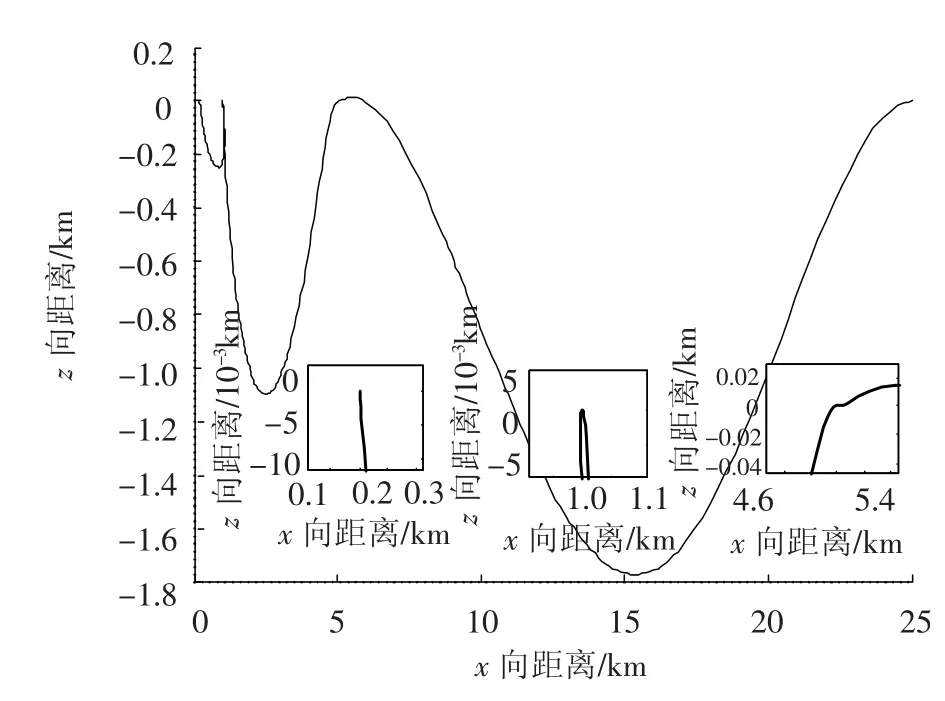
圖2 軌道交會的名義軌跡

圖3 名義速度隨時間的變化關系

圖4 名義控制變量隨時間的變化關系

圖5 航天器質量隨時間的變化關系

3.2 利用DA工具實現常微分方程積分仿真

本節以近地航天器圍繞地球的運動軌道為例，利用DA工具實現積分操作，航天器動力學方程為

航天器的初始軌道參數如表1所示，首先由初始軌道參數求出航天器的初始位置和速度，然后積分ODE方程得出航天器的運行軌跡，積分時間取一個周期T=6 556 s.為了說明利用DA工具對初值擾動進行靈敏度分析的效果，同時給出當x、y方向初始位置存在300 km偏差時的積分軌跡變化情況.

圖6和圖7分別給出了是否存在初值偏差時，利用DA工具所得到的積分曲線與直接利用ODE45進行積分的結果比較圖，從圖中可以看到，當不存在初值偏差時，曲線對于DA變量的階數并不敏感，而當x、y方向分別存在初值偏差為300 km時，隨著DA變量階數的增高(vorder=1、3、5時)，利用DA方法所得到的結果與針對不同初值重新進行ODE積分所得到的積分結果基本一致.但利用微分代數方法求解初始偏差對積分路徑的影響，只是采用了簡單的多項式代數操作，與重新對原始ODE方程進行積分運算相比運算量大大減少.

圖6 航天器運行軌跡3維示意

從圖8中不同階數下x方向的誤差得出，隨著時間的增加，積分誤差逐漸增大，但當vorder=5時，一個周期內的積分誤差可以保持在很小的范圍內.

圖7 航天器運行軌跡2維示意

圖8 x方向誤差對比

為詳細說明DA實現ODE方程的情況，下面給出當選取三階DA變量時，x方向上的Taylor展開系數如表3所示.

表3 x方向Taylor展開系數

由以上數據可知，5 224.003 981 650 331為不存在初值擾動時刻的航天器終止位置，經計算比較可見，經過1個周期后，航天器可返回原始位置，而當存在初值偏差時，對于終止位置的影響可以通過直接將偏差值代入Taylor展開式獲得，從而避免對應于每個不同的偏差值重新進行積分操作，可節省大量的計算量.當vorder越大，對于初值偏差的靈敏度分析越準確.為使結果精確，本文仿真中微分代數變量階數取為5.

3.3 存在點火時刻偏差時的航天器交會軌跡修正

由于各種原因致使航天器初始點火時刻與所求取的名義點火時刻可能存在一定的偏差，從而導致此時的軌道交會軌跡與名義軌跡偏差較大，無法完成給定交會任務.本文假定航天器在3個交會階段的點火時刻分別延后3 s、10 s、10 s情況下，首先給出此時實際位置軌跡與名義最優軌跡的對比.

從圖9中可以看出，隨著每個交會階段的誤差累計，最終的 x、z方向偏差分別在400 m和250 m左右，無法滿足交會要求，需要進行軌跡修正.下面給出利用微分代數方法求解的控制變量修正曲線以及修正后的交會軌跡.

圖9 軌道交會的軌跡對比

圖10為控制變量隨時間的變化，由圖中可以看出，修正后的控制變量軌跡與前者相差不大，一般在1E－5數量級，因此所消耗燃料情況與名義軌跡對應燃料消耗變化不大.通過對修正前后軌道交會的軌跡對比(如圖11所示)可知，航天器在位置保持點處的校正軌跡與名義軌跡基本一致，可以很好的解決由初始點火偏差導致的軌跡偏離問題，完成交會指標要求.

圖10 控制變量隨時間的變化關系

圖11 修正前后軌道交會的軌跡對比

4 結論

本文針對實際航天器軌道交會中脈沖推力假設失效情況，利用小推力推進系統實現航天器的燃料最少交會制導律設計.

1)首先利用直接法將控制變量離散，給出最優控制問題對應的狀態方程，約束條件和指標函數，并利用尋優函數得出最優控制變量和交會時間.從仿真結果可以看出，名義最優軌跡的位置和速度值基本滿足交會要求，航天器消耗燃料為26.6 kg.

2)其次本文給出了應用DA工具實現積分的具體方法，仿真結果顯示當存在初值擾動時，采用5階DA變量即可使得積分曲線與實際ODE45積分曲線基本一致.

3)最后針對軌道交會中的點火時刻誤差導致實際軌跡與名義軌跡有較大偏差的情況，利用微分代數方法，求取部分時間節點處控制變量的修正值，從修正后的軌跡可見，追蹤航天器在各個位置保持點的位置與名義軌跡相應位置基本重合，因此此法可以較好的實現軌跡修正，且應用DA求取控制變量的修正值，無需重新求解軌跡優化問題，只需簡單的多項式代數操作即可實現，從而節省大量的計算量，使得制導律的實現更為簡單易行.

[1]劉暾，趙鈞.空間飛行器動力學[M].哈爾濱:哈爾濱工業大學出版社，2003:83－101.

[2]HARI B H，MYRON T，DAVID D B.Guidance algorithms for autonomous rendezvous of spacecraft with a target vehicle in circular orbit[C]//AIAA Guidance，Navigation，and Control Conference and Exhibit 6 － 9.Montreal，Canada:AIAA，2001:1 －15.

[3]LOPEZ I，MCINNES C R.Autonomous rendezvous using artificial potential function guidance[J].Journal of Guidance，Control，and Dynamics，1995，18(2):237 －241.

[4]梁立波，羅亞中，唐國金.航天器近距離交會斜滑制導算法[J].國防科技大學學報，2009，31(5):125 －129.

[5]陳偉躍，荊武興，程博.小推力速度閉環交會制導律設計[J].宇航學報，2009，30(3):1030 －1038.

[6]BERZ M.Handbook of accelerator physics and engineering[M].New York:World Scientific，1999:81 －117.

[7]LIZIA P D，ARMELLIN R，ERCOLI-FINZI A.Highorder robust guidance of interplanetary trajectories based on differential algebra[J].Journal of aerospace engineering，sciences and applications，2008，1(1):43 －57.

[8]ARMELLIN R，LIZIA P D.Gravity assist space pruning based on differential algebra[J].Celestial mechanics and dynamical astronomy，2010，106(1):1 －24.