某型號摩托車車架有限元分析

陳 明，周 城

（浙江錢江摩托股份有限公司，a.摩托車事業部技術處，b.智能機械事業部技術處，浙江 溫嶺 317500）

摩托車車架作為承載基體，承受著傳遞來的各種力和力矩，是摩托車的核心部件。車架設計得好壞，對摩托車整體性能有直接的影響。車架的強度、剛度，對整車的乘坐舒適性、形勢安全性和可靠性直接相關。因此，車架的靜、動態強度和剛度設計，是車架設計的重要環節。

早期設計師在從事相關結構的設計時，通常是依據現有車型和研究者的經驗，對其作改進設計，并試制樣品，然后對實物反復進行各類靜、動態加載測試，逐步發現不合理區域，做有針對性的改進后，再試制。這樣的步驟，需要重復數次后，才能達到比較滿意的設計結果。

傳統的車架結構設計，采用的是類比的思想進行經驗設計。這種方法，只能得到近似解，而且精度低。

面對激烈的市場競爭，企業迫切需要運用現代先進的設計手段，以達到提高產品品質、降低設計成本的目的。研究表明，有限元法對解決上述問題，具有明顯優勢，由于計算機應用技術的快速提高，有限元法也得到迅速發展。隨著計算力學在行業中的應用，以及有限元理論的不斷完善和高水平配套軟件的出現，將有限元法應用到摩托車設計中已逐漸普遍。

下面以某110 mL 排量的彎梁車型車架為對象，介紹CAE 技術在該車架結構分析中的應用。

1 車架有限元模型的建立

1.1 車架的幾何特點

兩輪摩托車，根據形式不同可分為踏板式、彎梁式、跨騎式和越野式幾大類。其中踏板式和彎梁式車架比較接近，僅僅在車架尾部結構有不同的變化，圖1 為110 型摩托車車架結構CAD 圖。該車型采用彎梁式車架。

圖1 110 型摩托車車架結構圖

該車架部件主要采用管材和薄板鋼材沖壓而成，車架結構及其零件形狀各異，附屬零件多種多樣。在分析車架受力時，有些零件如掛鉤、支架等附屬設備，不必參與計算。因此，建立有限元模型前，需做一些簡化，這種簡化使計算的結果近似反映車架的真實受力情況；如果簡化不當，將造成很大的誤差，該誤差比有限元方法本身的誤差大得多。由此可見，合理地簡化模型，對計算結果的精度有很大影響。

1.2 車架網格劃分

將車架的CAD 模型導入Hyper Mesh 中經過幾何清理，去除不必要的附屬件，修補導入失敗的幾何單元，抽取中面后，就可以進行網格劃分。

對車架進行網格自動劃分時，對于較大的幾何模型，不能一次完成網格劃分，而又要保證品質，可以采取分塊劃分的方法。網格品質的好壞，直接決定了分析的精度，在Hyper Mesh 軟件中，可以很好地控制網格品質。劃分的方式，選用交互式。交互式的網格，允許在網格劃分結束后，通過修改參數來改變網格大小和分布。劃分好的網格模型如圖2 所示。

圖2 車架網格模型

劃分完成的車架網格模型，共有25 720個單元和26 521個節點。

2 車架靜態特性分析

2.1 靜態工況的建立

靜態特性分析，主要計算結構在固定不變的載荷作用下的應力、應變等的大小，即分析結構在受力后的響應情況，從而達到對結構強度、剛度的校核，以保證結構設計符合工作要求。

靜態工況包括力的施加，約束的建立，根據設計要求，以204 kg 總質量的負荷施加于車架的相應位置，包括駕駛員和成員的位置及發動機等較大零部件的位置等。為了保證求解的順利進行，要為模型施加約束條件，施加約束條件一般有如下兩點原則：

（1）要保證有足夠的約束，以消除結構的剛體位移；

（2）防止過約束。過多的約束，會導致計算結果出現不存在的反力。

綜合考慮，約束后擺臂軸自由度12 345，前輪軸自由度2 345。如圖3 所示。

圖3 車架約束示意圖

2.2 車架的靜態剛度

設定靜態分析的載荷步（loadstep）和相應的輸出參數，將CAE 模型提交求解器求解，在后處理中打開求解結果，即可看到車架的變形和受力情況。圖4 為車架變形示意圖，圖5 為車架應力分布圖。

圖4 車架變形示意圖

圖5 車架應力分布圖

2.3 計算結果及后處理

由車架應力分布圖可以看出，車架最高應力194.2 MPa。車架所使用的材料為Q235，該材料的屈服極限為235 MPa，表明在滿載情況下，車架應力未達到材料的屈服極限，車架普遍應力為43.2 MPa，存在可以優化的空間，最大應力發生在發動機下掛板、后擺臂間接連接板、座墊承載管三者的交匯處，可適當考慮通過改變形狀、增加厚度或者調整材料等措施，改善該部位應力較大的情況。

3 車架模態分析

結構系統的動力響應，可用固有模態進行組合，因此在動態響應分析中，模態分析十分重要。模態分析的結果，是判斷多種動態行為的根據，也是進一步分析（如瞬態分析、隨機振動分析）的數據基礎。模態是結構的固有特性，每個模態具有特定的固有頻率、模態振型和阻尼比，模態參數的獲得，可以通過計算或試驗取得，如果該過程是由計算的方法取得的，則稱為計算模態分析，如果是通過試驗取得的，則稱為試驗模態分析。

模態基本方程的求解，是一個求解廣義特征值問題，求解方法很多，如跟蹤法（Tracking Method），變換法（Transformation Method），以及蘭索斯法（Lanczos Method）等。

其中，蘭索斯法是跟蹤法和變換法的結合，具有較好的性能，所以很多軟件默認蘭索斯法為其求解算法，在軟件分析中，特征值問題的方程表示為

蘭索斯法是一種矢量正交化方法，對給定的矩陣以及起始量，可得到如下矢量序列

稱為克瑞勞夫序列（Krylov Sequence）。

當n→∞時，次序列收斂至特征矢量，以及最接近s 的特征值λ。

模態分析所使用的模型與靜力學分析的模型相同，但在模態分析時，需要設定材料的彈性模量。模態分析有兩種類型：約束模態和自由模態。

約束模態是指在對分析結構施加約束情況下提取的模態，而自由模態是不加約束時提取的模態。不加約束時結構的前六階為剛體模態，其模態頻率為0，而約束模態結果的第一階頻率，即是結構的模態頻率。本節計算車架的自由模態。

去除所有施加的約束，建立載荷步（loadstep）時選擇模態提取方法為蘭索斯法。由于對車架影響較大的頻率為前幾階頻率，因此本文提取前六階模態，計算結果如表1 所示。

表1 車架各階模特頻率

車架各階模態陣型如圖6。

車架一階頻率為30.64 Hz，振型如圖6 所示，在改模態頻率下，車架以圍繞中軸支撐點的扭轉為主，二階模態頻率為42.36 Hz，以側向彎曲為主，其余各階振型和頻率不一一列舉，摩托車行駛在路上，其路面激勵多在3 Hz 以下，摩托車的經濟車速在ν=40 km/h，路面的主頻帶為

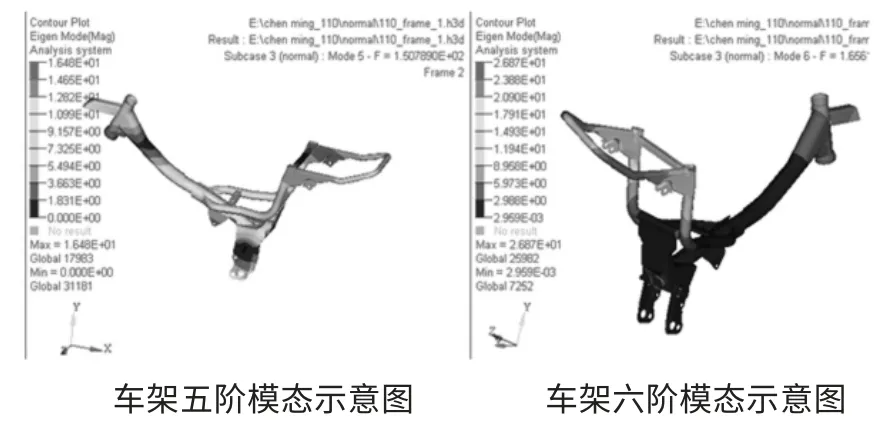
圖6 車架各階模態振型示意圖

Ω=0.1～0.2 次/m，

則輸入的時間頻率

f=ν Ω=1～22 Hz，

因此一階頻率大于該范圍，可以避開路面激勵引起的共振。

4 結束語

通過建立車架結構的有限元模型，并進行靜態特性分析，得到該車架的應力應變情況，為其結構優化提供了依據。同時通過模態分析，得出車架的低階頻率，為頻率優化提供指導，從而避免因路面激勵而產生的共振現象，有效地提高摩托車的乘坐舒適性和耐久性。將有限元方法引入車架設計可以為摩托車車架優化以及產品實驗分析提供參考依據與指導方向，并縮短產品的開發周期，節省大量研發經費。

[1]陳 瑞，王海麗，龔應忠. 運動型摩托車車架的有限元分析[J].傳動技術，2009，（6）：18-20.

[2]王 良，王 健.沙灘摩托車車架的有限元模態分析[J].山東理工大學學報（自然科學版），2004，（3）：46-50.

[3]張勝蘭，鄭冬黎，郝 琪，李楚琳. 基于Hyper Works 的結構優化設計技術[M].北京：機械工業出版社，2008.

[4]劉懷恒.結構及彈性力學有限元法[M].西安：西北工業大學出版社，2007.

[5]徐 睿.摩托車車架的有限元強度分析[J].重慶工學院院報（自然科學版），2007，（11）：34-37.