基于幅值限定積分器的永磁同步電機直接轉矩控制系統

孟高軍

(東南大學，江蘇南京 210000)

0 引言

1985年，直接轉矩控制理論被德國魯爾大學的德彭布羅克教授首次提出。直接轉矩控制技術在很大程度上解決了矢量控制中電機參數影響較大，旋轉變化非常復雜，以及實際中應用和理論結果不一致的現象。直接轉矩控制技術誕生以后，由于具有新穎的控制思想，簡潔明了的系統結構，優良的動、靜態性能而受到了普遍注意，得到了迅速發展。目前，該技術已成功應用在電力機車牽引的大功率交流傳動上。德國、日本、美國都開始發展此項技術，預計21世紀中旬會有較大發展［1］。

與矢量控制技術不同的是矢量控制誕生以后，很快應用到了永磁同步電機上，直接轉矩控制提出以后，并沒在永磁同步電機上得到應用［2-3］。直接轉矩控制開始在永磁同步電機上應用是在1998年由胡育文教授和湯立新博士提出永磁同步電機直接轉矩控制理論以后。在直接轉矩控制系統中，需要計算定子磁鏈，構成磁鏈自控制;需要定子磁鏈實現電機電磁轉矩的準確觀測;電機低速運行時需要定子磁鏈構成磁鏈量的閉環控制，以實現系統低速時定子磁鏈量的控制。因此，定子磁鏈的準確獲得是實現直接轉矩控制系統高性能的轉矩動態響應的關鍵因素之一。為此，學者們開始進行了更為深入的研究和拓展，形成了一系列新型改進磁鏈觀測器。在各種改進模型中，以Jun Hu和Bin Wu二人在1998年提出的一系列改進觀測器較為全面［4］，本文主要介紹的是他們提出的幅值限定的積分器，并針對該積分器在系統應用中存在的不足，提出了一種改造方案。

1 基于幅值限定積分器的直接轉矩控制

1.1 幅值限定積分器的原理和構造

改進型積分器的結構如圖1所示。其輸入變量為反電勢，輸出變量為定子磁鏈。這種改進積分器的基本思路可以通過式(1)來表示［5］:

圖1 幅值限定的積分器

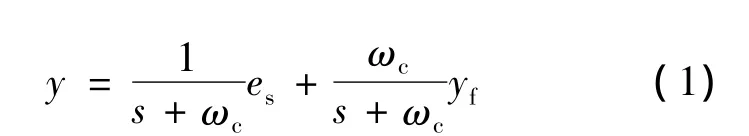
式中:es——積分器輸入信號;

yf——反饋信號。

這些觀測器采用反饋方式來改善磁鏈觀測精度。假設反饋信號為0的話，此時的積分器為一節慣性濾波器。若當觀測器輸出y作為反饋信號，那么改進積分器相當于純積分器。故適當選擇反饋信號，改進積分器就會獲得較純積分器和一節慣性濾波器更為優越的性能。

為了減小輸出定子磁鏈的相位失真，該積分器對觀測的定子磁鏈矢量幅值進行飽和限幅，而觀測的磁鏈相位不失真地反饋到輸入端，因此對信號相位沒有影響。該方案有效解決了磁鏈波形畸變問題，從而改善了積分器輸出信號的質量。但是該方案還存在磁鏈幅值及飽和基準之間的設定問題，磁鏈估計的準確性仍然受到飽和限幅基準選取的影響，且該算法要求電機磁鏈幅值恒定，不適用于電機磁鏈幅值變化的場合。

1.2 基于不同的直接轉矩控制的仿真結果與比較

先對帶有純積分器的永磁同步電機直接轉矩控制采用MATLAB/Simulink進行仿真［6］，然后用幅值限定積分器代替原有的純積分器再次仿真，得出兩者的仿真結果，并進行比較。圖2～圖5就是關于兩種不同積分器下的磁鏈軌跡和轉速波形。由圖可看出采用幅值限定的積分器的磁鏈軌跡更加圓滑，轉速波形更加平穩。其中電機參數如下:np=4，Rs=2.70，Ld=0.6mH，Lq=3.0mH，ω=40 rad/s。從圖2～圖5可明顯看出，采用幅值限定積分器比用純積分器有更好的性能。如果不改變其他參數，把電機轉速從原來的 40 rad/s增大到100 rad/s，然后再觀察磁鏈軌跡和轉速波形，如圖6和圖7所示。

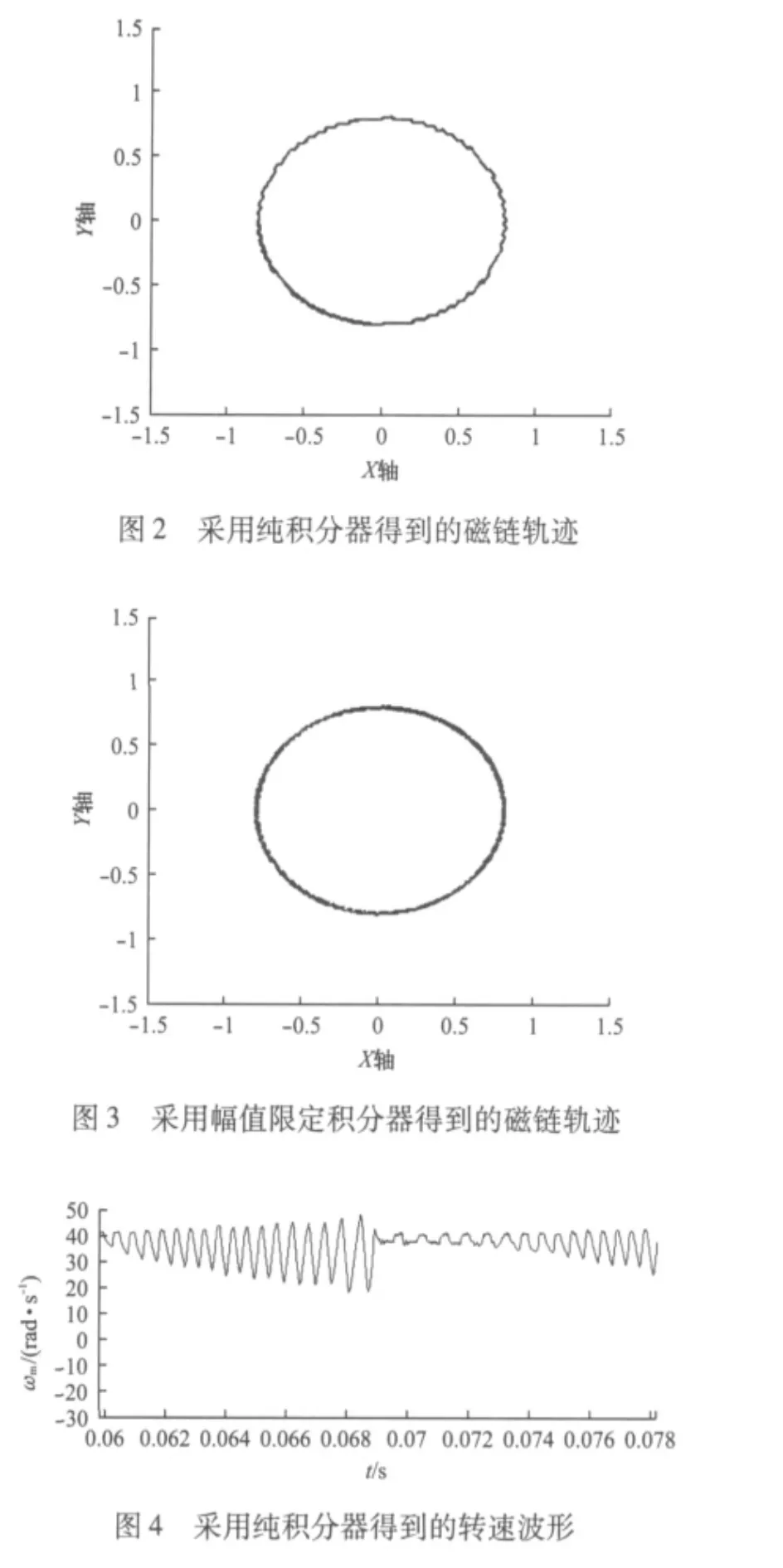
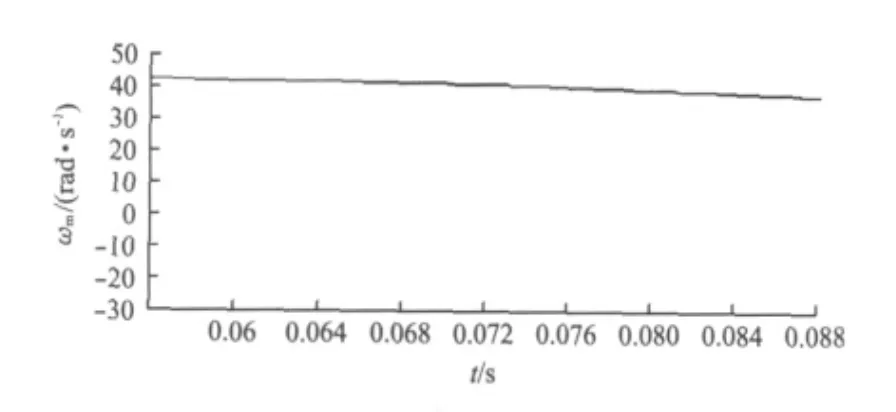
圖5 采用幅值限定積分器的轉速波形

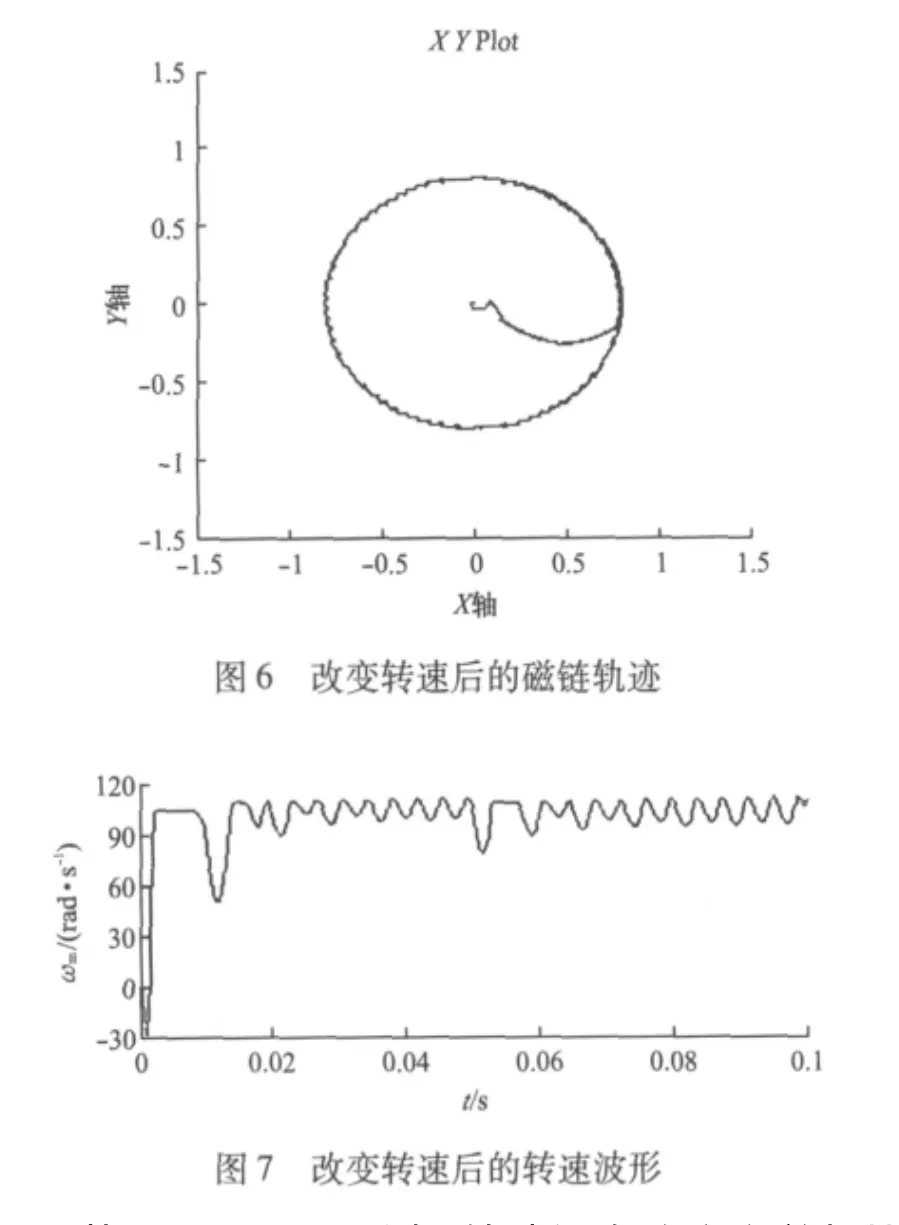
從圖6、圖7可看出，轉速沒有改變之前相比磁鏈軌跡已經不再圓滑，而轉速也已經不再穩定，出現了很大的波動。通過閱讀資料和分析，可以得出出現這種情況的原因，下面對原因進行具體分析。

由前文可知式(1)為幅值限定的改進積分器的基本原理，以α相為例，可以把式(1)寫成如下形式:

如果假設ψ'α為tψα，其中t為常數且大于零，那么式(2)可化簡為

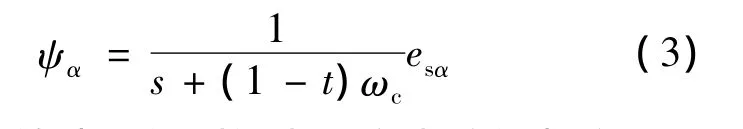
對于不同的轉速所得到的電壓和電流的頻率是不同的，故所得到的電動勢es的頻率也是不同的，即使截止頻率ωc相同，由式(3)可看出，所得到的ψα幅值仍然不同，由于ψα幅值不同，同理可得到ψβ幅值也是不相同的，最后可以推出對于幅值限定的改進積分器所得到的磁鏈幅值|ψ|也是不相同的，但仍將其與保持不變的磁鏈給定值進行比較，故將會造成控制性能下降甚至失敗的情況。

2 基于幅值限定積分器的改進方案

2.1 改進原理

針對上述情況，可以考慮運用狀態方程來求得定子磁鏈幅值，然后與給定磁鏈進行比較，這樣就可以避免上述不利因素，得到空間電壓矢量選擇表的一個輸入量，如果全部采用狀態方程，那么磁鏈的相位就無法確定，考慮到幅值限定的改進積分器對于相位的確定是非常準確的，所以仍然把幅值限定積分器作為確定磁鏈相位的工具，再加上狀態方程確定磁鏈幅值，兩者一起可以得到很好的效果。

永磁同步電機在d-q坐標系下的電壓和磁鏈的方程為

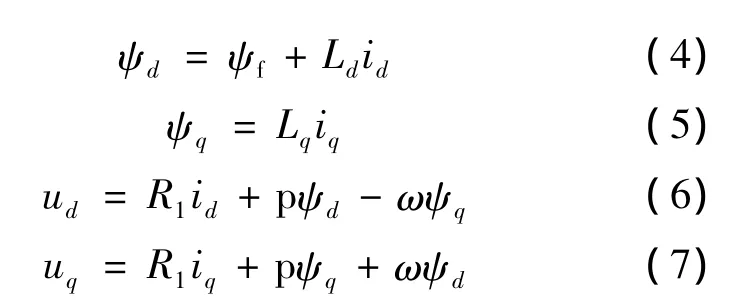
式中:ω——轉子旋轉電角速度;

p——微分算子。

由式(4)和式(5)可得

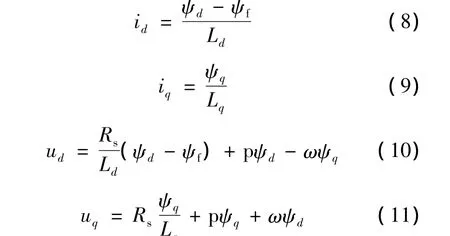
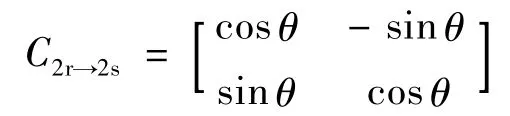
2.2 改進后的仿真模型和仿真結果

圖8為改造后的永磁同步電機直接轉矩控制系統，為了方便認識和理解，對于這個模型，做出了詳細的標注。

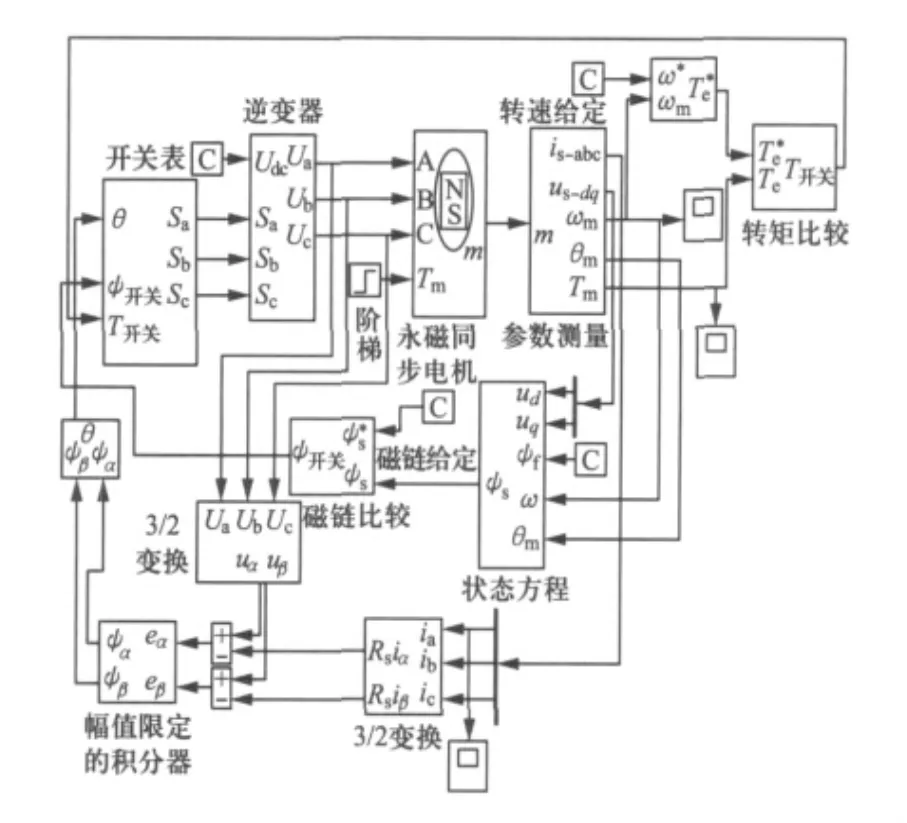
圖8 改造后的永磁同步電機直接轉矩控制系統

針對上述改進積分器下的直接轉矩控制模型進行仿真，圖10和圖11分別為改進之后，在100 rad/s的轉速下的磁鏈軌跡、轉速波形的仿真結果。通過改進后的磁鏈軌跡和轉速波形可以很明顯地看出，當轉速變為100 rad/s時，在幅值限定的改進積分器下，直接轉矩控制仍保持了很好的性能。

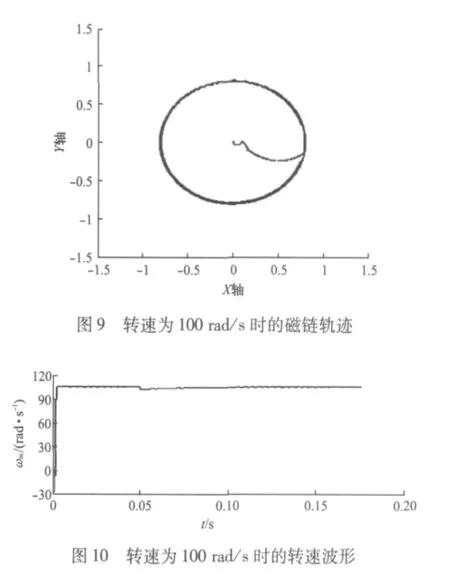
3 結語

本文主要是對永磁同步電機直接轉矩控制系統的仿真模型建立和仿真結果進行分析，首先對純積分器、幅值限定積分器，這兩種不同積分器下的直接轉矩控制進行仿真，并且比較他們的磁鏈軌跡和轉速波形。如果不改變其他參數，把轉速提高到100 rad/s，幅值限定的積分器的性能和效果會變得很差，故提出了狀態方程和積分器共同作用，由狀態方程確定磁鏈幅值，由積分器來確定磁鏈相位，以取代之前只依靠積分器判斷磁鏈幅值和相位的方法。通過仿真發現經過該方法改進后取得了很好的效果。

［1］陳伯時，陸敏遜.交流調速系統［M］.北京:機械工業出版社，1998.

［2］ZHONG L，RAHMAN M F，HU W Y，et al.Analysis direct torque controller for permanent magnet synchronous motor drives［J］.IEEE Transactions Energy Conversion，1997，14(3):637-640.

［3］田淳，胡育文.永磁同步電機直接轉矩控制系統理論及控制方案的研究［J］.電工技術學報，2002，17(1):7-11.

［4］楊永明，孫才新，李新.局部放電在線監測中干擾的識別及抑制方法的研究［J］.儀器儀表學報，1999，20(3):242-243.

［5］HU J，WU B.New integration algorithms for estimating motor flux over a wide speed range［J］.IEEE Trans on PE，1998，13(5):969-977.

［6］李三東，薛花，紀志成，等.基于MATLAB永磁同步電機控制系統的仿真建模［J］.江南大學學報，2004，21(2):44-45.