用最低費用加快法求解成本—工期優化

薛俊鋒

（邯鄲市邯三建筑工程有限公司，河北 邯鄲 056001）

1 問題的提出

網絡計劃的優化,是通過不斷調整和改善,使之達到成本最低、工期最短的過程。在一般項目施工中要加快某項工作,通常都需要增加勞動力、材料供應、機械設備等,而這些增加均會引起成本的增加,因此工程成本與工期有著密切的關系。對某一個項目而言,既不能簡單地認為縮短工期就會增加成本,也不能認為延長工期就會降低成本,所在地就存在一個時間與費用的優化問題,即網絡計劃工期與成本的優化。

2 工期-成本的關系

（1）工期—成本的關系曲線。工期成本時由直接費用和間接費用組成的，一般情況下，壓縮工期將引起直接費用的增加和間接費用的減小；反之，延長工期會使直接費用減小，直接費用增加。

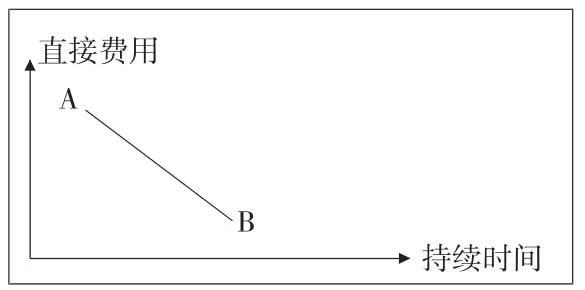
圖1 工作持續時間與直接費用曲線

（2）費用率。為簡化起見，通常可用直線AB表示工作持續時間與直接費用的關系（如圖1）。任意一項工作的費用率ei-j，反映該工作縮短（或延長）單位持續時間所需增加（或減少）的費用數額，即ei-j=（mi-j-Mi-j）/（Di-j-di-j）其中，Mi-j和mi-j表示持續時間變化前后的直接費用，Di-j表示壓縮前的持續時間，di-j表示縮短后的持續時間。

3 優化方法

工期成本優化是以工程成本最低為前提尋求工期最優的優化方法。其基本方法是，從網絡計劃的各工作持續時間和費用關系中，依次找出一方面既能使工期縮短，另一方面又能使得費用增加最少的工作，不斷地壓縮其持續時間，同時考慮間接費的增加，即可求出工程成本最低時的相應最優工期。關鍵路線的持續時間決定工期的長短，因此壓縮工期首先應縮短關鍵路線的持續時間，而且，首先應壓縮費用率最小的關鍵工作的持續時間，即“最低費用加快方法”。

4 實例分析

某工程雙代號網絡計劃如圖2所示，圖中箭線下方括號外數字為工作的正常時間，括號內數字為最短持續時間；TF為某工作總時差。間接費率為1.45萬元/天。各工作的工期一成本數據列于表1中，計算后所得的費用率e也列于表1中。現對其進行費用優化。

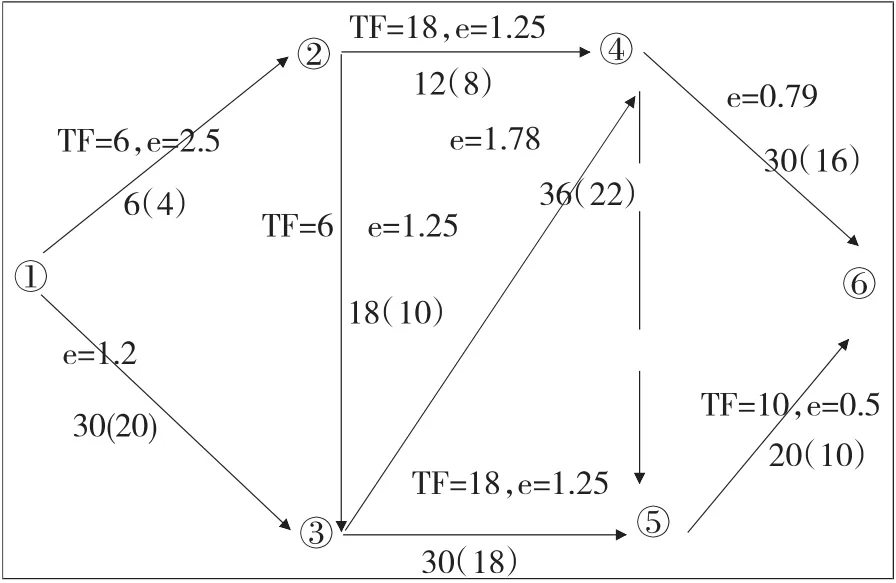
圖2 某網絡計劃圖

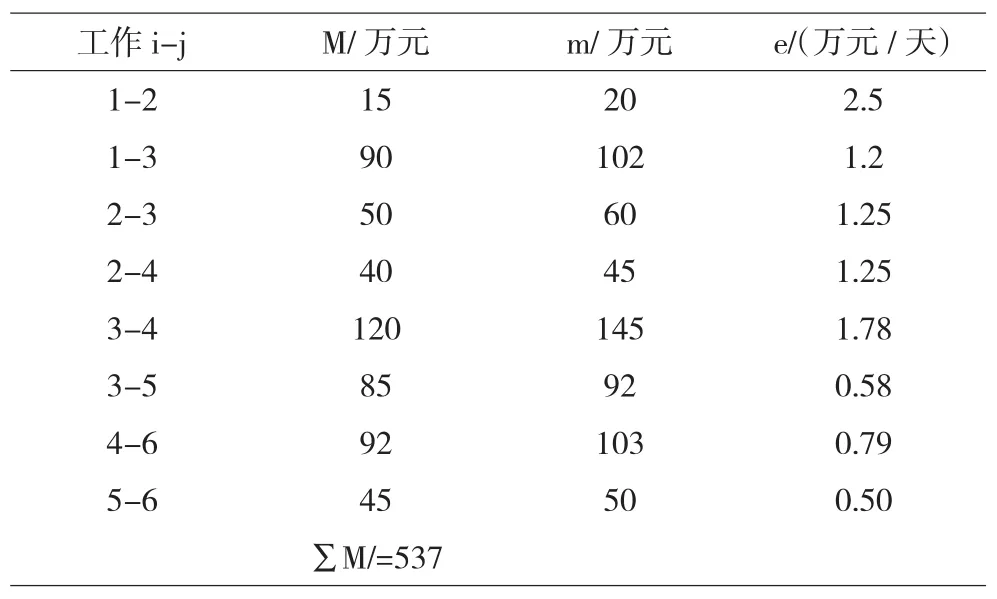
表1 各工作的工期成本數據表

網絡計劃費用優化可按以下步驟進行：

（1）第一次壓縮：從圖3可知，該網絡計劃中關鍵線路為①→③→④→⑥，費用率最小的關鍵工作為④→⑥，e4-6=0.79。工作④→⑥的持續時間可壓縮30-16=14天，但是由于工作⑤→⑥的總時差只有10天，所以△t1=min<14,10>=10天

則△S1=e4-6*△t1=0.79*10=7.90 萬元，S1=△S1+S0=537+7.90=544.90萬元。

第一次壓縮后，圖2變為圖3

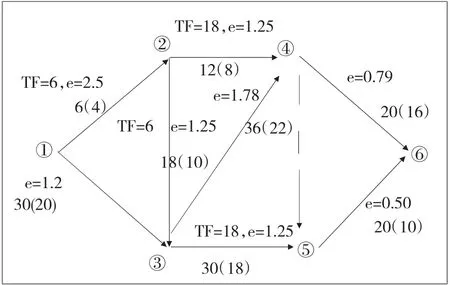
圖3 第一次壓縮后的網絡計劃圖

（2）第二次壓縮：在圖3中，有兩條關鍵路線，分別為①→③→④→⑥和①→③→④→⑤→⑥。第一條線路上e最小值e4-6=0.79，第二條線路上e最小值e5-6=0.50，則∑e=0.79+0.50=1.29，所以宜壓縮工作①→③。工作①→③的持續時間可壓縮30-20=10天，但工作②→③的總時差為6天，因此工作①→③的壓縮時間為△t2=6天。則△S2=e1-3*△t2=1.20*6=7.20萬元，S1=△S1+S0=544.90+7.20=552.10萬元

（3）第三次壓縮：第二次壓縮后，網絡圖更新為圖4，在該圖中關鍵線路有4條，能縮短工期的切割方案有4種，即：

AA切割，∑e=1.2+2.5=3.7

BB切割，∑e=1.25+1.2=3.75

CC切割，∑e=1.78

DD切割，∑e=0.79+0.5=1.29

因此，選擇e最小的方案，即DD方案。

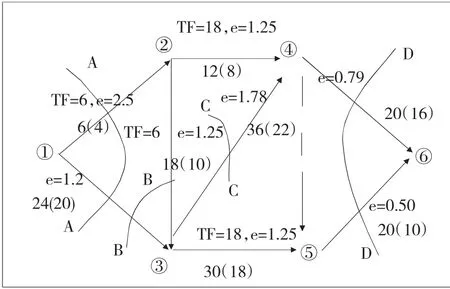
圖4 第二次壓縮后的網絡計劃圖

工作④→⑥可縮短4天，工作⑤→⑥可縮短10天，所以t3=min<4,10>=4天

△S3=∑e*△t3=1.29*4=5.16萬元，S3=S3+S0=552.10+5.16=558.26萬元

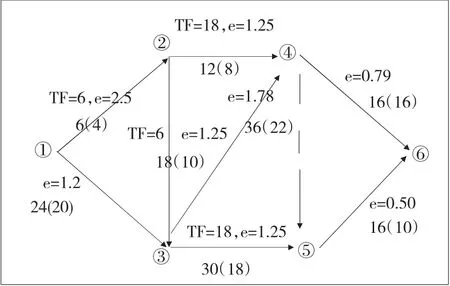
圖5 第三次壓縮后的網絡計劃圖

經過三次壓縮，原網絡圖最終變為如圖5所示，工期變為76天。

將上述優化過程中的結果及相應的間接費匯于表2中，可知最優工期為80天，工程成本為668.1萬元。

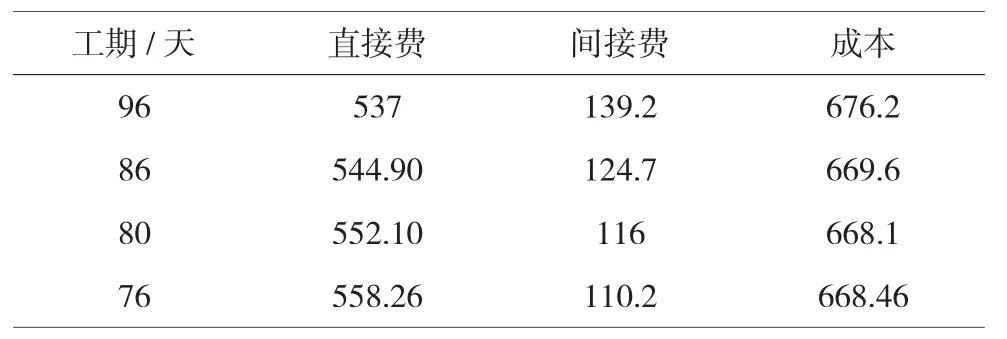
表2 優化后的工期成本數據表

5 結語

我們可以看到，工期成本優化主要是通過系統擇優壓縮原理，利用費用率從總體上進行同步壓縮，不斷壓縮工程的直接費率，從而尋求滿足要求的最優方案的過程。為縮短工程建設時間、控制工程成本提供了有效解決辦法。