案例教學(xué)法在高職數(shù)學(xué)教學(xué)中的應(yīng)用

李建杰

案例教學(xué)法在高職數(shù)學(xué)教學(xué)中的應(yīng)用

李建杰

北京電子科技職業(yè)學(xué)院 北京 100029

案例教學(xué)法是從實(shí)際問題出發(fā)，經(jīng)過合理簡捷的推導(dǎo)歸納，從而引出數(shù)學(xué)知識。采用案例教學(xué)法，不僅可以激發(fā)學(xué)生的學(xué)習(xí)興趣，引導(dǎo)學(xué)生積極主動地參與學(xué)習(xí)過程，提高教學(xué)質(zhì)量，而且有利于提高學(xué)生解決問題的能力，提升數(shù)學(xué)素養(yǎng)。

高職數(shù)學(xué)；案例教學(xué)；教學(xué)實(shí)踐

10.3969/j.issn.1671-489X.2012.36.107

作者：李建杰，副教授，研究方向?yàn)閿?shù)學(xué)教育。

Author’s addressBeijing Polytechnic, Beijing, China 100029

1 問題的提出

高等數(shù)學(xué)作為高職院校一門重要的基礎(chǔ)理論課程，它所提供的思想方法、理論知識不僅是學(xué)生學(xué)習(xí)專業(yè)課程的重要工具，也是培養(yǎng)學(xué)生創(chuàng)新能力的有力支撐，并為學(xué)生的終身學(xué)習(xí)奠定基礎(chǔ)。依據(jù)高職教育的人才培養(yǎng)目標(biāo)，數(shù)學(xué)課程的教學(xué)必須以強(qiáng)化知識應(yīng)用為導(dǎo)向，以培養(yǎng)學(xué)生的應(yīng)用能力為目標(biāo)，突出數(shù)學(xué)知識與實(shí)際應(yīng)用、相關(guān)專業(yè)內(nèi)容的契合。

近年來，隨著高職院校的擴(kuò)招，學(xué)生的數(shù)學(xué)基礎(chǔ)較之過去有所下降，且水平參差不齊，導(dǎo)致高等數(shù)學(xué)的教學(xué)目標(biāo)很難實(shí)現(xiàn)。怎樣做才能實(shí)現(xiàn)教學(xué)中既能準(zhǔn)確地講授概念及公式的推導(dǎo)等知識，又能提高學(xué)生的學(xué)習(xí)興趣，使學(xué)生比較容易地掌握并運(yùn)用它們解決問題？著名教學(xué)論專家孔德拉秋克曾經(jīng)說過，教學(xué)的成敗在很大程度上取決于教師能否妥善地選擇教學(xué)方法。因此，在高等數(shù)學(xué)的教學(xué)中，教師如何運(yùn)用適當(dāng)、科學(xué)的教學(xué)方法，就成為提高教學(xué)效果的基礎(chǔ)與條件。

在總結(jié)教學(xué)經(jīng)驗(yàn)的基礎(chǔ)上，受到案例教學(xué)法的啟發(fā)，筆者發(fā)現(xiàn)：在講授數(shù)學(xué)概念及一些公式的推導(dǎo)時，如果能充分采用直觀的案例教學(xué)，可使概念的講解言簡意賅、公式的推導(dǎo)深入淺出，有利于激發(fā)學(xué)生學(xué)習(xí)的積極性和探索精神，啟迪學(xué)生的思維，拓寬學(xué)生的視野，幫助他們系統(tǒng)地理解并掌握相應(yīng)的數(shù)學(xué)知識和思維方法。

2 案例教學(xué)法在高等數(shù)學(xué)教學(xué)中的優(yōu)勢

案例教學(xué)法主要是教師圍繞特定的教學(xué)、培訓(xùn)目的，把實(shí)際中真實(shí)的情景加以典型化處理，形成供學(xué)生思考分析和決斷的案例，通過獨(dú)立研究和相互討論的方式，來提高學(xué)生分析問題和解決問題的能力。教師引導(dǎo)學(xué)生探究的過程就成為講授數(shù)學(xué)基礎(chǔ)知識的過程，二者融為一體。

與傳統(tǒng)的教學(xué)方法相比，案例教學(xué)法具備5個優(yōu)勢：

1）案例教學(xué)法可以把抽象概念置于一定的情景之中，使學(xué)生清楚地認(rèn)識到所要學(xué)的概念在實(shí)際生活、專業(yè)課中的用處與表現(xiàn)形式；

2）案例教學(xué)法不僅僅是讓學(xué)生簡單地掌握理解概念，而且更注重培養(yǎng)學(xué)生的探究精神和解決問題的能力；

3）學(xué)生通過案例教學(xué)得到的知識不是外界強(qiáng)加給的，而是內(nèi)化了的知識；

4）案例教學(xué)能啟發(fā)學(xué)生的思維，調(diào)動學(xué)生的學(xué)習(xí)興趣，使艱澀的數(shù)學(xué)教授過程從“要我學(xué)”轉(zhuǎn)變成為“我要學(xué)”；

5）案例教學(xué)法縮短了教學(xué)情景與實(shí)際問題情境的差距，有利于扭轉(zhuǎn)學(xué)生普遍認(rèn)為學(xué)數(shù)學(xué)只是紙上談兵的錯誤思想。

3 案例教學(xué)法在高等數(shù)學(xué)教學(xué)中的可行性

從高等數(shù)學(xué)發(fā)展歷程不難看出，高等數(shù)學(xué)是伴隨著其他學(xué)科的發(fā)展而發(fā)展的，高等數(shù)學(xué)的諸多進(jìn)展當(dāng)初更是順應(yīng)其他學(xué)科發(fā)展對數(shù)學(xué)工具的需求應(yīng)運(yùn)而生的，因此它天生具有廣泛的應(yīng)用性。從這個角度看，高等數(shù)學(xué)除了“基礎(chǔ)性”以外還具有“工具性”的一面，它是學(xué)生后續(xù)學(xué)習(xí)專業(yè)課程的工具。因此，培養(yǎng)學(xué)生應(yīng)用數(shù)學(xué)的意識和能力已成為數(shù)學(xué)教學(xué)的重要方面。在案例教學(xué)的實(shí)施過程中，案例的選擇與案例的使用是需要解決的核心問題。

3.1 案例的正確選擇

要組織好案例教學(xué)，最基本的是選擇好案例，選擇案例時要充分考慮四方面的因素。

一是目的明確。教學(xué)中所用到的案例不僅要符合教學(xué)目標(biāo)和教學(xué)內(nèi)容的需要，而且要符合學(xué)生的認(rèn)知水平，利于學(xué)生理解知識，并能夠運(yùn)用所學(xué)知識解決類似問題。

二是趣味性強(qiáng)。通過對本院學(xué)生的問卷調(diào)查顯示，學(xué)生對由實(shí)際問題引入數(shù)學(xué)知識都懷有濃厚的興趣，但普遍存在畏難情緒。針對這一特點(diǎn)，在收集案例時，選擇那些既有趣味又能充分體現(xiàn)數(shù)學(xué)思想方法的簡單案例，從培養(yǎng)興趣著手，讓學(xué)生逐步體會到解決問題的方法和數(shù)學(xué)的重要性。

三是具有代表性和廣泛性。案例教學(xué)要盡量避免涉及過多的專業(yè)知識，同時要考慮到當(dāng)今科學(xué)技術(shù)的發(fā)展、學(xué)科間的互相滲透。這些問題的實(shí)際背景容易被學(xué)生了解和接受，有的就是平時有所接觸但又未深入了解的普通問題，學(xué)生產(chǎn)生濃厚興趣，從而愿意去深入了解。

四是具有真實(shí)性。學(xué)習(xí)數(shù)學(xué)的目的在于培養(yǎng)學(xué)生解決實(shí)際、專業(yè)中的問題，因此，案例選擇的真實(shí)性和實(shí)用性尤為重要。

3.2 案例教學(xué)法的正確運(yùn)用

根據(jù)荷蘭數(shù)學(xué)教育家弗來登塔爾的數(shù)學(xué)教育思想，數(shù)學(xué)教育應(yīng)該從學(xué)生的數(shù)學(xué)現(xiàn)實(shí)出發(fā)，從生活的現(xiàn)實(shí)出發(fā)，通過提出問題、分析問題、探究討論直至解決問題，經(jīng)過概括提高，升華為數(shù)學(xué)概念、數(shù)學(xué)法則及數(shù)學(xué)思想。高等數(shù)學(xué)中的許多概念都有良好的物理背景或幾何背景，教學(xué)時結(jié)合學(xué)生已有的數(shù)學(xué)知識和生活經(jīng)驗(yàn)，充分利用這些資源，引導(dǎo)和啟發(fā)學(xué)生去發(fā)現(xiàn)和探究，揭示其中所包含的由特殊到一般，由具體到抽象的辯證過程，從而使學(xué)生了解數(shù)學(xué)概念的來龍去脈，體驗(yàn)數(shù)學(xué)概念的形成過程，領(lǐng)悟其中蘊(yùn)涵的數(shù)學(xué)思想。

例如，講解定積分的概念時，筆者選擇下面的案例組織教學(xué)。

1）提出問題。建造一座橫截面如圖1所示的拱橋，假設(shè)界面的拱頂為拋物線型，橋孔為一矩形上加一半徑為r的圓弓。試計(jì)算砌此橋的截面墻需用磚的數(shù)量。

2）分析問題。這看起來是一個簡單的初等幾何問題。先計(jì)算出橋的橫截面積，再除以磚的橫截面積，就可以得到需要磚的數(shù)量。

橋的橫截面積=拋物線AmF下的面積-矩形BCDE的面積-圓弓CnD的面積

這里，學(xué)生通過已有知識，能求出矩形BCDE的面積和圓弓CnD的面積，而拋物線下所圍面積，如何解決？

圖1

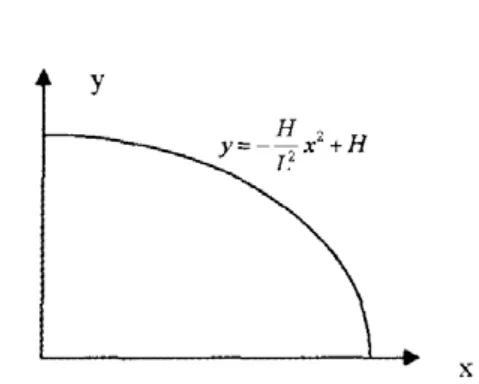
圖2

圖3

4）探究與討論問題。

①教師先向?qū)W生呈現(xiàn)高等數(shù)學(xué)事例。德國天文學(xué)家開普勒發(fā)明了一種求圓面積的方法：把圓分割成無窮多小扇形，小扇形可近似用小的等腰三角形來代替。學(xué)生從中受到啟示，即局部以直代曲以及化整為零、積零為整的思想。再要求學(xué)生求出圖3所示曲邊梯形的面積。學(xué)生想到用一些小矩形來近似求出它的面積，用4個小矩形的面積之和代替。于是，另一個學(xué)生說要想誤差更小，分割的小矩形越多越好。

②恰當(dāng)利用現(xiàn)代教學(xué)手段，將自我探索引向深入。演示隨著矩形個數(shù)的增加，這些小矩形所組成的臺階型面積就越逼近拋物線下的面積的動畫過程，使得在黑板上較難表現(xiàn)的函數(shù)極限過程得到較好的展示，使抽象的教學(xué)內(nèi)容變得直觀、生動、形象。

③引導(dǎo)學(xué)生分析、討論。通過探究過程學(xué)生體驗(yàn)：分割的意義是化整為零；近似代替的目的曲轉(zhuǎn)化為直；求和的作用是積零為整；求極限的目的是直轉(zhuǎn)化為曲，獲得精確數(shù)值。

④自主與合作學(xué)習(xí)，教師給予必要的指導(dǎo)。

下面請同學(xué)們一起計(jì)算面積A：

繼續(xù)這種作法……

把區(qū)間[0,1]n等分，則臺階型面積：

⑤引導(dǎo)學(xué)生歸納反思。曲邊梯形的面積與給定區(qū)間、分割方法、取點(diǎn)的關(guān)系。求曲邊梯形的面積體現(xiàn)了曲轉(zhuǎn)化為直，直轉(zhuǎn)化為曲，以及由此所反映出來的化整為零、積零為整的思想方法，是微積分乃至整個高等數(shù)學(xué)的一個重要方法。

通過實(shí)驗(yàn)對比，運(yùn)用案例教學(xué)法的學(xué)生在此基礎(chǔ)上舉一反三，把解決單一問題得出的結(jié)論、方法和思路應(yīng)用于解決更多的實(shí)際問題的能力明顯強(qiáng)于對照班的學(xué)生。

案例教學(xué)法是在實(shí)際問題求解的鋪墊下構(gòu)建數(shù)學(xué)知識，不僅能使學(xué)生了解知識產(chǎn)生的背景，而且能夠體驗(yàn)知識的探究過程，強(qiáng)化了對學(xué)生運(yùn)用數(shù)學(xué)知識解決問題能力的培養(yǎng)，在實(shí)際教學(xué)實(shí)踐中是切實(shí)可行的，值得重視和推廣。

[1]云連英.微積分應(yīng)用基礎(chǔ)[M].北京:高等教育出版社,2006:92.

[2]席振偉.數(shù)學(xué)的思維方式[M].南京:江蘇教育出版社,1995:6.

[3]富成華,崔殿軍.高職高等數(shù)學(xué)“案例與實(shí)驗(yàn)”教學(xué)法初探[J].遼寧高職學(xué)報(bào),2007(6):17-18.

Application of Case-based Method to Mathematical Teaching of High Vocational School

Li Jianjie

Case-based method is intended for solving problems in practice. Mathematical thinking can be used in the process of reasoning and concluding. By applying case teaching method, teachers can not only evoke students’ interest, encourage participation in the study, but can also help improve the students’ ability to analyze practical mathematical problems.

mathematics of high vocational school; case-based method; teac hing practice

G712

B

1671-489X(2012)36-0107-03