一種基于彼得羅夫伽遼金公式的三角形單元★
賈 程
(鹽城工學院土木工程學院,江蘇 鹽城 224051)
0 引言
傳統的等參有限單元模型滿足變分一致性要求,能夠較好的分析許多實際的問題,但是存在剛度矩陣過剛、對網格畸變敏感等問題。剛度矩陣過剛帶來了自鎖問題和計算精度下降問題,對于線性三角形單元尤其明顯。對網格畸變敏感要求劃分問題域的網格質量較高,如四邊形單元要求其夾角盡量保持90°,這給前處理帶來巨大的工作量。為了改善上述缺陷,學者們提出了許多方法:hybrid-Trefftz單元法[1]、無網格法[2]等,然而,這些方法還有局限性或不夠完善的地方。
在實際應用時,工程師比較偏愛三角形單元。因為它們能夠被自動的生成。本文使用非對稱有限單元公式的概念,將線性三角形單元形函數和有限元無網格耦合三角形單元(FE-LSPIM TRI3單元)形函數分別作檢驗函數和試函數,構造出基于彼得羅夫伽遼金公式的US-FE-LSPIM TRI3三角形單元。
1 US-FE-LSPIM TRI3三角形單元公式
1.1 FE-LSPIM TRI3三角形單元的形函數

圖1 支持域的定義
對于二維線彈性問題,采用三角形網格離散問題域,如圖1所示。單元內任一點的位移可表示成:

其中,N′=[N1,N2,N3]是傳統的線性三角形單元的形函數矩陣是由三個節點坐標決定的常數;ue={u1(x,y) u2(x,y) u3(x,y)}T是局部節點位移函數。在該節點處等于其位移值,即:ui(xi,yi)=ui,i=1,2,3。局部節點位移函數ui(x,y)利用Rajendran等[3]使用的最小二乘點插值無網格法(LSPIM),由i點的支持域內的節點值擬合得到:

其中,φi=[φi1φi2φi3…φiN],i=1,2,3,ui=[u1u2u3L uN]T。
其中,φi是LSPIM法的關于節點i的形函數矩陣;ui是節點i支持域內節點的位移參數向量;N為節點i支持域內的所有節點數。一個單元所有節點支持域的合集構成了一個單元的支持域Ω。
節點支持域和單元支持域的定義分別如圖1所示。
將方程(2)代入式(1)得:

從方程(3)中,可以得到該單元的形函數矩陣,設單元支持域Ω內的節點數為M:

局部節點位移可以寫成下列形式:
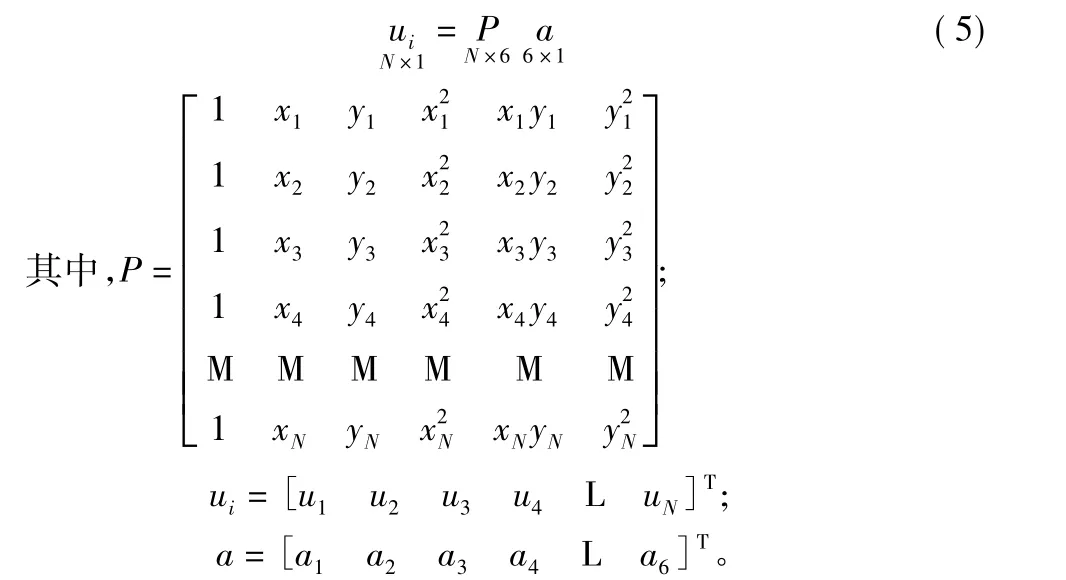
令該單元的第一個節點記為節點i。由于傳統的最小二乘近似a=(PTP)-1PTui使得節點i的位移近似值不等于該點的位移值,即ui≠p(xi,yi)a,導致位移條件施加比較困難。故為了使節點i的位移近似值等于該點的位移值,利用方程(5)中的第一個方程解出a1,再從方程(5)其余的方程中消去a1,并由最小二乘法得:

其中,φi為局部節點位移函數的形函數;1為所有元素均為1的(N-1)行列向量;和的定義和文獻[3]中相似,只是少了x2y和xy2項。利用式(4)進而可以求出單元的形函數矩陣ψ。
根據式(6)可以得出,在(xi,yi)點存在 ui(xi,yi)=ui,再根據式(4)可得FE-LSPIM TRI3三角形單元的形函數ψ具有Kronecker delta性質,能夠像普通的有限元一樣直接施加位移邊界條件。
1.2 US-FE-LSPIM TRI3三角形單元公式
線彈性體系平衡狀態的虛功方程為:

其中,δu為虛位移域;δε為響應的虛應變域;σ為真實應力。
由于ψ為線性三角形單元形函數和點插值無網格法形函數的復合函數,具有高階的完備性,ψ插值的應力函數σ^比線性三角形單元的應力函數更加適合作試函數。對于檢驗函數,只要其滿足邊界條件和域內連續條件,故選擇線性三角形單元形函數插值的虛位移域δ做檢驗函數。
將它們代入式(7),并整理得:

2 檢驗算例
2.1 受彎矩作用的懸臂梁
如圖2a)所示懸臂梁,在端部受常彎矩M=20C2作用,彎矩形式分布在右端,尺寸L=100,C=10,彈性模量 E=1.0 ×107,泊松比 μ =0.3,ρ=8 000 kg/m3,考慮平面應力狀態。

圖2 端部受彎矩的懸臂梁
采用2×6×2,2×10×2,4×16×2,6×20×2,8×28×2五種形式的三角形網格劃分問題域,為了與四邊形等參元比較,本問題也采用相應的2×6,2×10,4×16,6×20,8×28五種四邊形網格劃分。圖2b)為2×6×2網格劃分示例。A點的位移計算結果列于表1。

表1 A點的位移
從表1中可以看出,US-FE-LSPIM TRI3單元能夠很好的重構常彎矩下的解,而傳統的線性三節點三角形單元(T3)和四節點等參四邊形單元(Q4)的結果不夠精確。
2.2 Cook懸臂梁
本例為變截面的懸臂梁,在端部受一個分布剪力F=1/16作用,如圖3a)所示。彈性模量E=1.0,泊松比μ=1/3。本問題采用2×2×2,4×4×2,8×8×2,16×16×2四種三角形網格劃分形式。圖3b)所示為4×4×2的形式。

圖3 Cook懸臂梁
不同網格下A點的最小主應力列于表2。相比于T3和Q4單元,US-FE-LSPIM TRI3單元顯示了最佳的結果。

表2 A點的最小主應力
3 結語
使用非對稱有限單元法的概念,構造出基于彼得羅夫伽遼金公式的US-FE-LSPIM TRI3三角形單元。由于線性三角形單元形函數和FE-LSPIM TRI3單元形函數插值的位移函數能夠滿足域內位移連續性和完備性的要求,選擇它們分別作為檢驗函數和試函數。數值算例顯示,該US-FE-LSPIM TRI3三角形單元精度較高,優于傳統的線性三角形單元和四邊形等參元。
[1] FREITAS J A,BUSSAMRA F L S.Three-dimensional hybrid-Trefftz stress elements[J].International Journal for Numerical Methods in Engineering,2000,47(5):927-950.
[2] 張 雄,胡 煒,潘小飛,等.加權最小二乘無網格法[J].力學學報,2003,35(4):425-431.
[3] RAJENDRAN S,Zhang B R.A“FE-meshfree”QUAD4 element based on partition of unity[J].Computer Methods in Applied Mechanics and Engineering,2007,197(1-4):128-147.
[4] Timoshenko S P,Goodier J N.Theory of Elasticity[M].3rd edn.New York:McGraw-Hill,1934.
[5] 庫 克,馬爾庫斯,普利沙.有限元分析的概念與應用[M].關正西,強洪夫,譯.第4版.西安:西安交通大學出版社,2007.

