窄帶干擾條件下水聲OFDM系統LMMSE信道估計算法＊

寧小玲 劉 忠 付學志

（海軍工程大學電子工程學院 武漢 430033）

0 引 言

在高速的無線數據傳輸中，正交頻分多路復用（OFDM）技術因具有頻帶利用率高和抗多徑衰落能力強等優點，目前已廣泛用于無線局域網、無線廣域網等［1］.OFDM技術應用于水下自組網的水聲通信也是大勢所趨［2］.信道估計是OFDM系統中補償水下聲信道畸變的一項非常重要的技術，這方面的研究已經取得了一定成效［3］.現有的導頻信道估計方法在對系統進行實際分析時常忽略一些干擾，如窄帶干擾（NBJ），從而導致不客觀的結論［4］.目前，對處于窄帶干擾條件下的OFDM系統信道估計方法的研究還不多［5］.本文重點討論了窄帶干擾條件下的一種線性最小均方（LMMSE）估計方法，揭示了其參數的物理意義，這種改進的LMMSE估計不需要事先知道信道的統計特性和噪聲的方差，并避免了大矩陣的求逆運算，能用于實際系統中.

1 基于梳狀導頻的OFDM系統LS和LMMSE估計

在梳狀導頻輔助的信道估計中，設OFDM系統具有N個子載波，M個導頻子載波信號均勻地插入頻域傳輸信號中，插入等間隔長度L＝N／M，對于每一個OFDM符號，它的第k個子載波頻域傳輸數據和導頻子載波信號可以表示為［6］

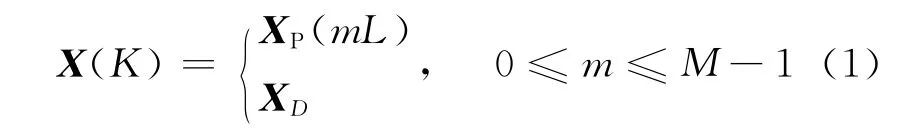
式中：X（k）為第k個子載波頻域傳輸信號；XD為數據；XP（mL）為第m個導頻.

假設OFDM系統不存在窄帶干擾，在頻域內的接收信號為

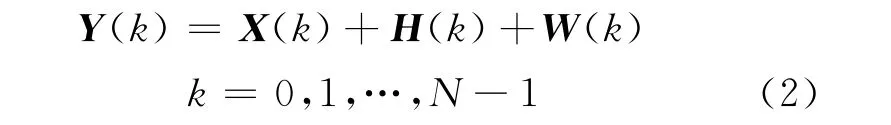
LS信道估計是最簡單的一種信道估計方法，它的導頻估計表達式為

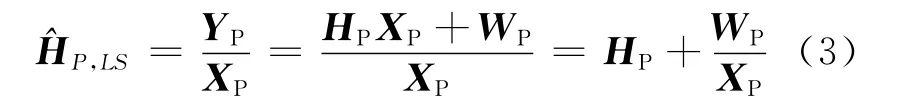
可見＾HP，LS實際上是導頻處被零均值AWGN所污染的真實信道響應的觀察值，所以它受噪聲的影響大，在信噪比較低時估計精度和性能不高.

LMMSE信道估計是最優的線性估計器［7］，它本質是用信道的自相關矩陣對LS信道估計進行修正，抑制噪聲對估計值的影響.在文獻［8］中提到，信道響應h是高斯的并且與信道噪聲不相關，則信道響應h在導頻位置上的LMMSE估計可簡化為

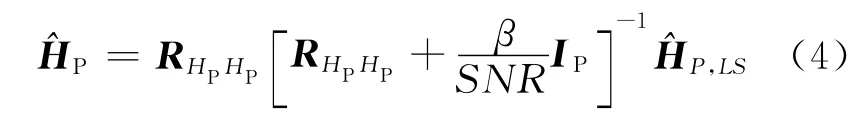
式中：＾HP＝［＾H1，＾H2，…，＾HM］T；IP為單位矩陣，信噪比SNR＝E［｜XP｜2］／；β＝E｜X（k）｜2E｜1／X（k）｜2是星座因子，對于BPSK和QPSK信號，β＝1，對于16QAM，β＝17／9.

2 窄帶條件下的LMMSE估計

窄帶干擾的出現是由于窄帶干擾信號的帶寬小于OFDM塊中一個子載波的帶寬，即：BJ≤BS.其中：BJ和BS分別是窄帶干擾信號和一個子載波的帶寬.和式（2）對應，窄帶干擾條件下每一個子載波經過離散傅里葉變換（DFT）后可簡化為

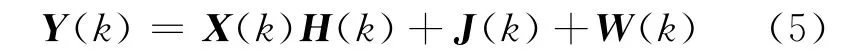
相應地，在導頻位置上的信道估計為

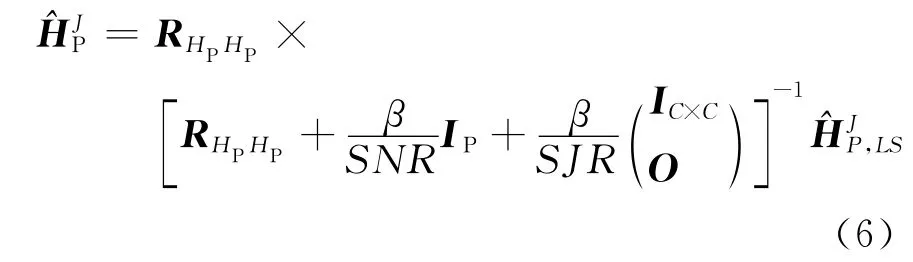
信道的自相關矩陣RHPHP由多徑信道的功率和時延τi所決定的.假設信道每條路徑是相互

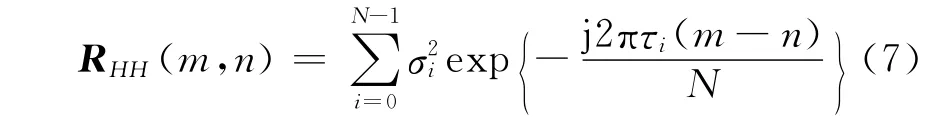
式中：RHH＝［RHH（i，j）］N×N，是一個循環矩陣.對于LMMSE估計器，如果能夠測出第i徑的幅度方差，就不必矩陣求逆運算，節省了很大的計算量.文獻［9］進一步提出了一種簡化的近似等價LMMSE算法，也稱最有效抽頭（MST）算法，該算法首先對得到的梳狀導頻LS信道估計值進行IFFT 變換獨立的，其能量為.頻域信道響應H（k）自相關矩陣可表示為

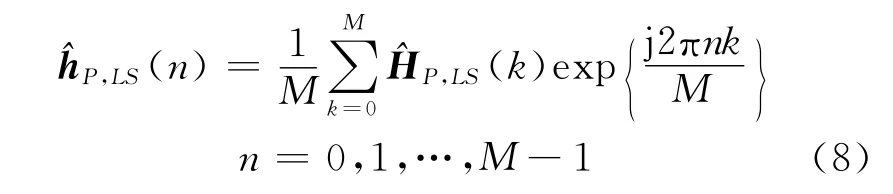
然后把最重要的g個信道抽頭保留下來，其余的信道抽頭置零.

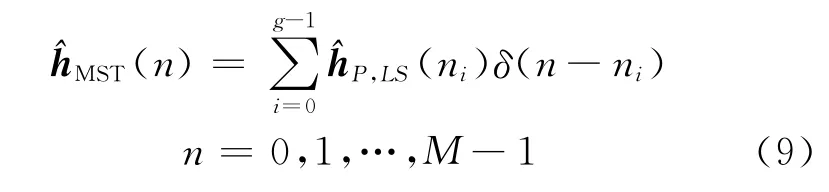
該算法相比LS算法能夠減少AWGN噪聲干擾的影響，但是它可能會選擇錯誤的信道抽頭而把正確的忽略.因為在窄帶干擾環境下，那些能量大的信道抽頭很可能被窄帶干擾污染，在這種情況下，得到的信道估計值用在內插濾波中，導致更加嚴重的估計誤差.

對于SNR和SJR的測量，在文獻［4］提出的窄帶干擾條件下干擾導頻探測方法中，涉及了對干擾信號功率σ2J的近似計算.

3 改進LMMSE算法

從第1節的分析可知，為了對多徑信道進行合理估計，必須估計出第i徑的幅度方差以及SNR和SJR.

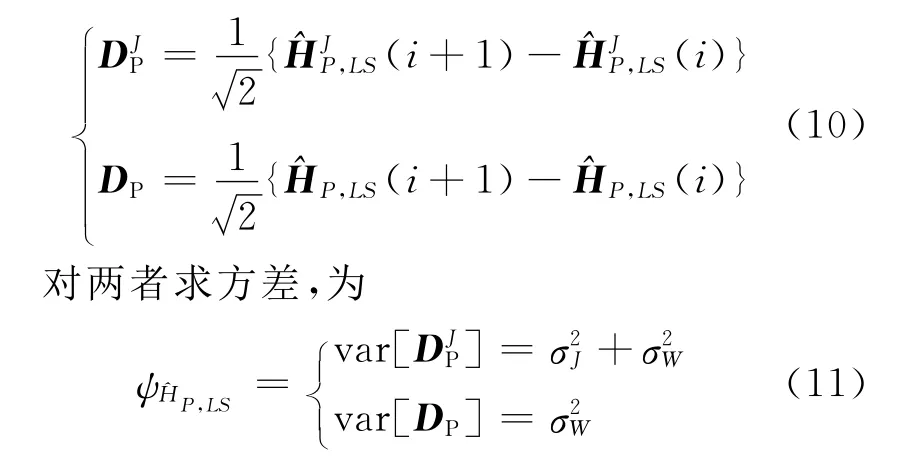
為了求出自相關矩陣RHPHP，在文獻［6］的基礎上進行改進.從前面的分析中可知對于每一個OFDM符號，有M－C個沒有被窄帶干擾信號污染的＾HP，LS，所以，本文的改進方法是先把受干擾的時域估計值置零

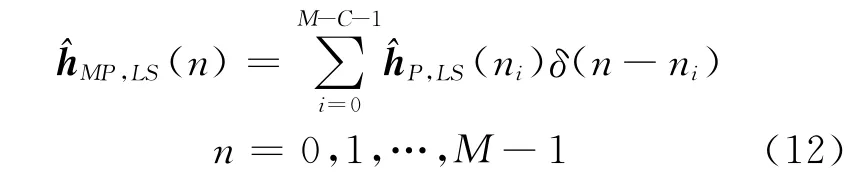
在求出＾hMP，LS（n）基礎上，利用文獻［9］提出的方法，消除未受干擾的時域信道估計值中的噪聲影響.文獻［9］中提到兩種選擇最有效信道抽頭的方法：（1）閾值選擇法，閾值的大小定為最大信道抽頭能量的η倍；（2）設計最有效抽頭數，通常選擇最有效抽頭數為多徑數的2倍.本文則采用閾值選擇法剔除受窄帶干擾的信道徑和消除白噪聲的影響，閾值分為窄帶干擾閾值λJ和白噪聲閾值λW，具體方法為：信道每一徑的能量大于λJ的視為受窄帶干擾的徑，小于λW的視為噪聲徑.（具體參數見仿真說明）.最終得到的信道時域為

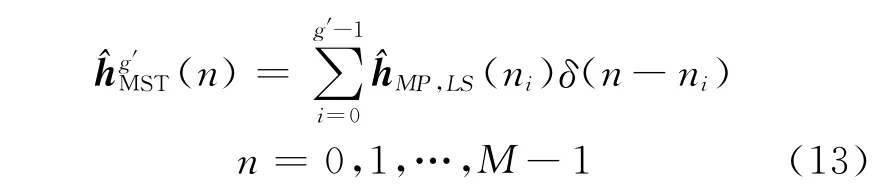
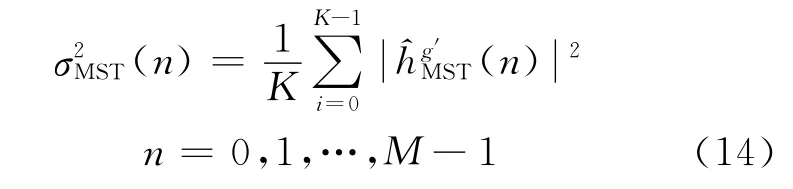
為了求得自相關矩陣RHPHP的估計值，可根據RHPHP是循環矩陣這個性質先求出它的第一行［RHPHP（0，0），RHPHP（0，1），…，RHPHP（0，M－1）］，用表示.和式（7）相對應，利用FFT和IFFT變換的關系，可以得到

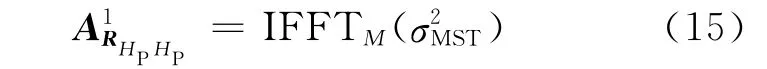
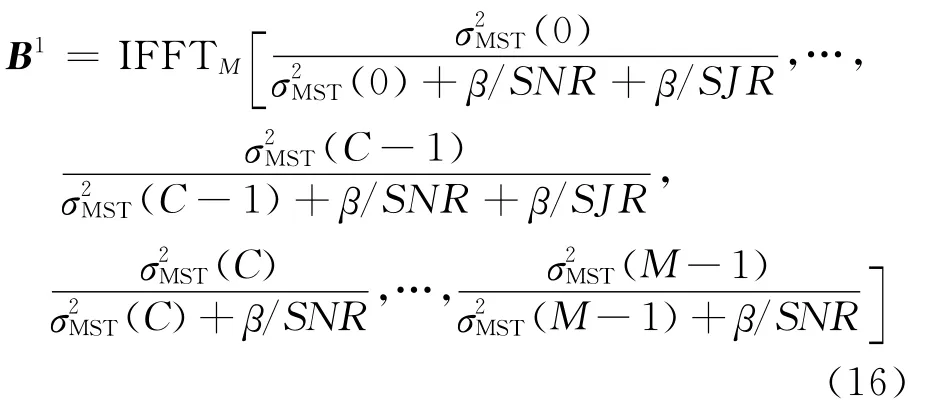
在求得導頻位置處的信道響應后，采用文獻［11］的線性內插信道估計算法恢復出所有位置的信道響應＾H.相應地，根據這K個信道估計向量，計算歸一化均方誤差（NMSE）.

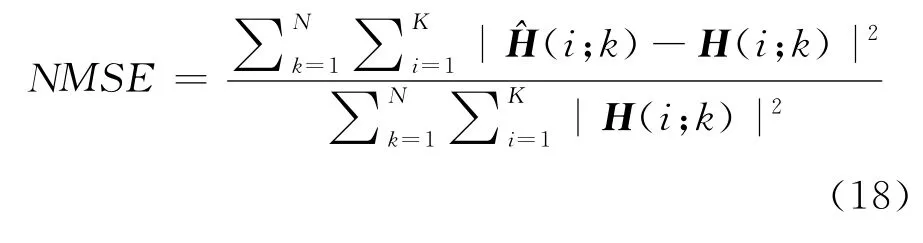
從而求得矩陣.對于K個OFDM符號，可以得到K個MMSE信道估計

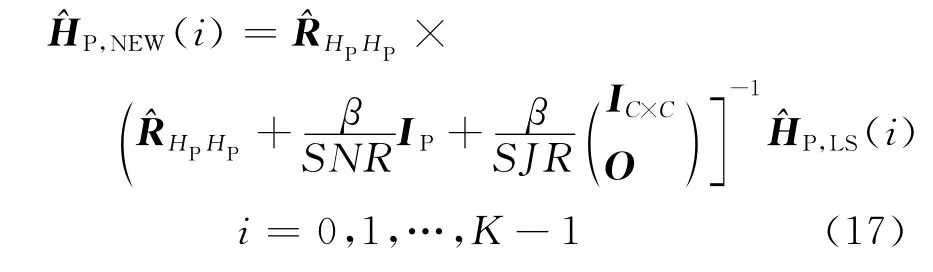
4 仿真結果及分析

仿真信道采用文獻［12］的負聲速梯度水聲信道模型進行仿真.為了得到信道估計性能，假設接收機實現完全同步.同時，為了避免碼間干擾，選擇保護間隔大于信道的最大延遲.仿真中采用的系統參數如表1所列.

表1 系統參數

文獻［9］比較了不同閾值 MST LMMSE算法的MSE性能，本文選擇閾值η＝5×10－3對其進行仿真，消除白噪聲的影響，并與本文的Proposed LMMSE算法進行比較.Proposed LMMSE算法排除白噪聲徑的閾值定為λW＝，排除受窄帶干擾的信道徑閾值定為.

圖1比較了MST LMMSE算法和Proposed LMMSE算法的BER性能.由圖1可以看出，MST LMMSE算法相比Proposed LMMSE算法受窄帶干擾影響嚴重.MST LMMSE算法在SNR≥10dB后，不同的窄帶干擾條件下，BER性能相差較多，而Proposed LMMSE受影響較小；在同樣的白噪聲條件下，2種算法的BER性能相差明顯.可見，Proposed LMMSE可以剔除窄帶干擾對導頻信號的影響，有較強的抑制窄帶干擾能力.

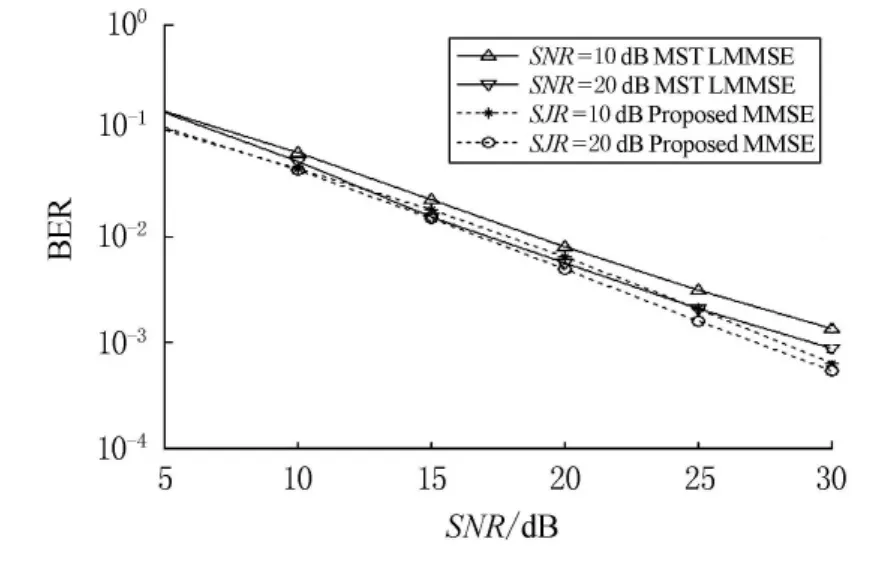
圖1 MST LMMSE和Proposed LMMSE的BER性能比較

圖2對LS算法、文獻［4］提出的Proposed LS算法、LMMSE算法以及Proposed LMMSE算法的BER性能進行了比較.從圖中可以看出，LS信道估計抑制噪聲的能力比較差，所以其BER性能也是最差的；LMMSE信道估計，假設已知每條多徑的幅度方差和時延的前提下，獲得最優的信道相關矩陣，因此性能也是最優的；Proposed LS估計算法剔除了窄帶干擾的影響，BER性能比LS算法有很大提高，但是由于沒有完全剔除噪聲的干擾，在BER性能為10－2時相比Proposed LMMSE算法有約7.5dB的差距；Proposed LMMSE算法相比LMMSE在 低于10dB之前，BER性能約有1dB的差距，隨著 提高，BER性能差距增大到2dB.可見，Proposed LMMSE算法在低信噪比（白噪聲干擾嚴重）條件下的估計性能與理想的LMMSE算法更接近，而相比Proposed LS算法約有7.5dB的增益，這種特性使得該算法在實際水聲系統應用中具有更大的優勢.

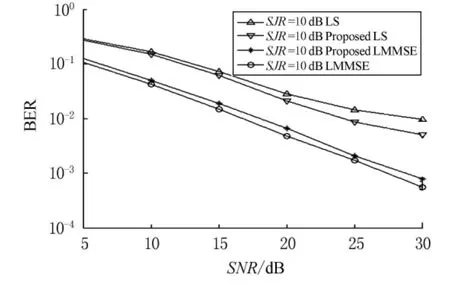
圖2 4種信道估計方法BER性能比較

圖3比較了各種算法在SNR＝20dB時，MSE隨SJR變化的性能曲線.各種算法的MSE性能和圖2分析的BER性能一樣依次增強.值得注意的是，圖3顯示在低SJR條件下，LS信道估計和Proposed LS估計算法相差很大；LMMSE信道估計和Proposed LMMSE估計算法相差甚微，在SJR∈（0～10）dB的范圍內，兩者只有約2 dB的MSE性能差異.而隨著SJR慢慢變大，兩組算法的變化趨勢正好相反.這說明了越是在強的窄帶干擾條件下，改進算法的效果越明顯.同時可看出，Proposed LMMSE相比Proposed LS在MSE性能為2×10－2時，相差約6dB，這是由于Proposed LMMSE除了能剔除窄帶干擾外，還可以排除其他白噪聲的干擾，而Proposed LS對白噪聲不敏感.綜合以上分析得出，由于不可能完全把干擾影響排除，Proposed LMMSE估計算法和LMMSE信道估計還存在一定差距，即便如此，Proposed LMMSE算法不需要已知RHPHP、SNR和SJR等信息，計算復雜度較低，比LS類有更好的估計效果，可用于實際系統中，因此，該算法具有較高的可靠性和應用價值.

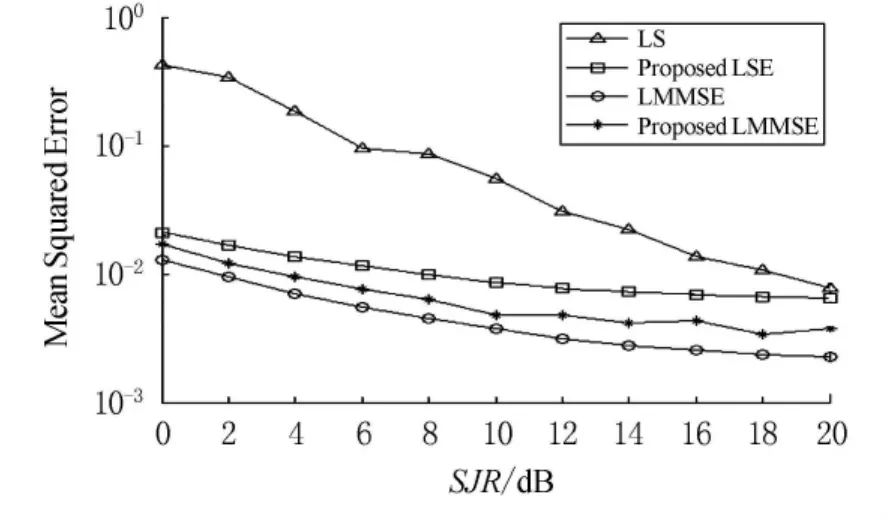
圖3 窄帶干擾對各種信道估計方法MSE的影響

5 結束語

本文從理論上討論了梳狀導頻LMMSE信道估計算法和LS信道估計算法的關系，及其參數分析.在此基礎上，分析了窄帶干擾條件下的LMMSE信道估計，得出一個簡單實用的LMMSE算法表達式.為了將該算法應用于實際系統中，通過LS信道估計的結果得到LMMSE估計事先需要知道的信道自相關矩陣，信道抽頭幅度以及噪聲能量，該方法不需要大矩陣的求逆運算，簡化了計算復雜度.通過仿真結果可見，本文提出的算法在強白噪聲和窄帶干擾條件下能夠達到幾乎和理想狀態下LMMSE信道估計的效果，相比LS信道估計，其估計效果要好得多，即使和理想狀態LMMSE信道估計還存在一定的距離，該算法仍然具有顯著的優勢，因此，該算法具有較大的實用價值.

［1］樊昌信，曹麗娜.通信原理［M］.6版.北京：國防工業出版社，2009.

［2］AKYILDIZ I F，POMPILI D，MELODIA T.Underwater acoustic sensor networks：research challenges［J］.Ad Hoc Networks，2005，3（3）：257－279.

［3］LI B，ZHOU S，STOJANOVIC M，et al.Multicarrier underwater acoustic communica－tions over fast－varying channels［J］.IEEE Journal of Oceanic Engineering，2008，33（2）：198－209.

［4］HAN M，YU T，KIM J，et al.OFDM channel estimation with jammed pilot detector under narrow－band jamming［J］.IEEE Transactions on Vehicular Technology，2008，57（3）：1934－1939.

［5］PATEL C S，STUBER G L，PRATT T G.Analysis of OFDM／MC－CDMA under imperfect channel estimation and jamming［C］／／Proc.of Wireless Communications and Networking Conference，Atlanta GA：IEEE Press，2004，2：954－958.

［6］LIU L，TAO C，QIU J，et al.A novel comb－pilot transform domain frequency diversity channel estimation for OFDM system［J］.Radioengineering，2009，18（4）：497－502.

［7］YANG B，CAO Z，LETAIEF K B.Analysis of lowcomplexity windowed DFT－based MMSE channel estimator for OFDM system［J］.IEEE Transactions on Com －munications，2001，49（11）：1977－1987.

［8］3GPP TR25.814，V7.1.0.Physical Layer Aspects for Evolved Universal Terrestrial Radio Access（UTRA）（Release7）［S］.2006.

［9］MINN H，BHARGAVA V K.An investigation into timedomain approach for OFDM channel estimation［J］.IEEE Transactions on Broadcasting，2000，46（4）：240－248.

［10］KUMAR R.A fast algorithm for solving a toeplitz system of equations［J］.IEEE Transactions on A－coustics Speech，and Signal Processing，1985，33（1）：254－267.

［11］COLERI S，ERGEN M，PURI A，et al.Channel estimation techniques based on pilot arrangement in OFDM systems［J］.IEEE Transactions on Broadcasting，2002，48（3）：223－229.

［12］郭業才.自適應盲均衡技術 ［M］.合肥：合肥工業大學出版社，2007.