減弱觀測誤差對回歸模型的影響研究

趙 卿，周興東

減弱觀測誤差對回歸模型的影響研究

趙 卿1，2，周興東1

（1.江蘇師范大學測繪學院，江蘇徐州 221116；2.江西省數字國土重點實驗室，江西撫州 344000）

對變形監測序列進行數據建模分析時，含有誤差的監測數據會對模型的建立產生較大的影響。提出一種“事件”模型改變原始觀測序列的表達形式，通過對原始觀測數據進行轉換，對變形監測數據按照某種規則進行分類劃分，劃分后的數據能夠適應Cox模型。根據經驗或者實際情況，適當調節“事件”模型參數，在一定程度上可以減弱觀測誤差帶給Cox回歸模型的影響，算例分析進一步論證了該模型計算結果的準確度能夠進一步地提高計算結果的準確度。

觀測誤差；變形監測；事件模型；Cox回歸模型

變形監測對觀測精度有很高的要求，而監測過程中不可避免受到外界條件干擾（如水汽等）而帶來觀測誤差，通過平差的方法可以消除每期觀測結果含有的偶然誤差，但是在整個監測時期內，監測點的觀測序列中含有的誤差仍然無法消除［1－2］，而且較大的誤差會對后續建模分析產生很大影響［3］；實際監測工作中，小波變換進行消噪是目前處理含有噪聲信息的監測序列較為常用的辦法［3］。該方法對減弱誤差對觀測序列的影響，具有很好的效果［4］。本文提出一種“事件”模型來變換監測序列，通過調節模型參數，可以減弱觀測誤差對數據分析結果的影響，應用Cox回歸模型計算［5－6］得到對變形數據分析的新方法。

1 建立“事件”模型

建立“事件”模型的假設為：上次“事件”的發生對下一次“事件”的發生遲早會產生很大影響［5，7］。在變形監測數據分析過程中，監測點在某時刻的變形信息，在一定程度上要受到前一時期內變形結果的影響。基于此假設，在變形監測數據分析中，對監測資料中的位移量建立如下“事件”模型。

（1）設監測資料中第i監測點在監測時刻j的位移量數據為δij（i＝1，2，…，n；j＝1，2，…，m），計算該監測點在相鄰觀測時刻間的平均位移速率vij（i＝1，2，…，n；j＝1，2，…，m－1），并以矩陣的形式表達，即

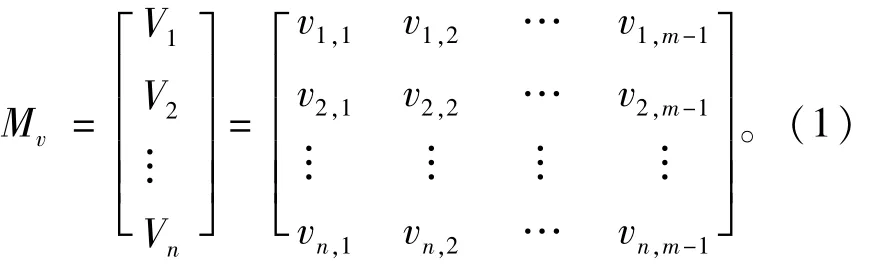
式中，Vi（i＝1，2，…，n）表示第i個監測點的位移序列。

（2）根據監測資料中各個監測點的平均位移速率vij（i＝1，2，…，n；j＝1，2，…，m－1），計算該監測資料的位移速率閾值

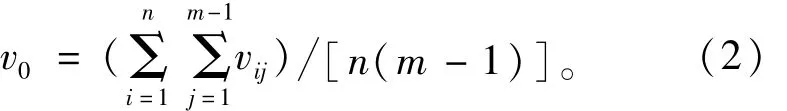
或者憑多年觀測經驗，給定一個位移速率的閾值v0，定義“監測點位移速率vij和給定閾值v0的比較結果”為“事件”，用eij（i＝1，2，…，n；j＝1，2，…，m－1）表示。

（3）對于第i個監測點，如果滿足“vij＜v0”，則稱監測點i在時刻j為“事件未發生”狀態，相應的eij＝0；如果滿足“vij＞v0”，則稱監測點i在時刻j為“事件發生”狀態，相應的eij＝1，即，以監測點位移速率vij與閾值v0的比較結果，決定各監測點的“事件”狀態，并把式（1）表達成“事件矩陣”其中，Ei（i＝1，2，…，n）表示第i個監測點的“事件”狀態序列。

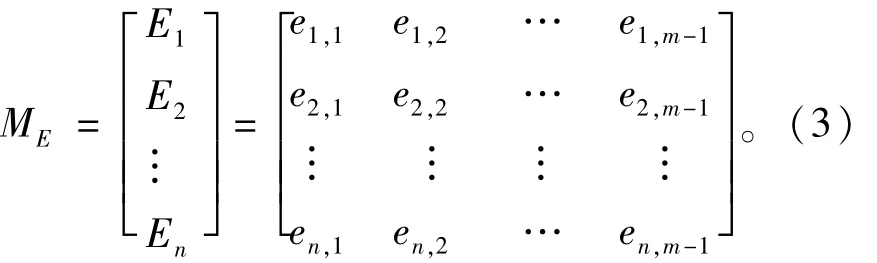
通過上述步驟（1）—（3），可以將原始觀測數據位移δij轉化成“事件”eij，完成“事件”模型的建立。

2 “事件”模型的優勢

分析“事件”模型的建立的過程，可以發現該模型在一定程度上可以減弱觀測誤差的影響。

變形監測的過程，不可避免地會有各類誤差源的干擾，尤其是在觀測條件較差的環境里，致使計算得到的位移數據帶有誤差。通過適當調整位移速率的閾值v0，可以有效減弱觀測誤差的影響。

例如，由于觀測條件較差（受水汽較大等影響），第i監測點在j時刻的Xij坐標含有誤差，設真值為為觀測值，觀測精度為σij，真誤差為εij，則

假定本期與上期觀測為等精度觀測，間隔為δtij＝tij－ti，j－1，則本期的位移為

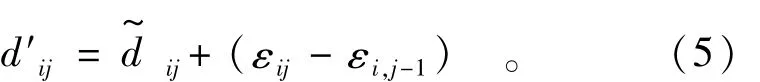
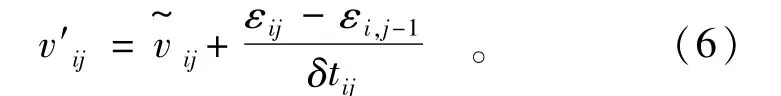
平均速率的精度為

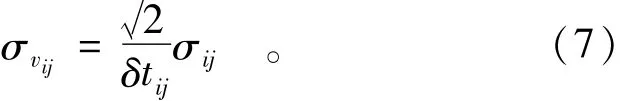
按照常規的分析計算（如回歸分析、時間序列等方法），以位移為研究對象，可以明顯看到由于觀測誤差εij影響，致使回歸模型在此刻的輸入數據δij中含有εij－εi，j－1誤差；如果建立“事件”模型，根據需要，調整位移速率的閾值v0，使得第i監測點在j時刻的“事件”狀態保持一致，不受原始觀測值含有的誤差之影響。例如調整閾值v0為

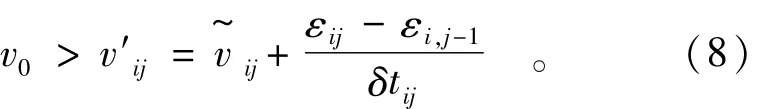
v0的調節范圍在，可以始終讓第i監測點在j時刻的“事件”狀態為eij＝0作為模型輸入，則可以有效減弱原始觀測誤差σ的影響。

由于各個觀測值含有的真誤差εij未知，則在調節閾值v0范圍時，參考式（7），可以取2倍于平均速率的中誤差作為調節限差；由于每個監測時期的觀測精度σij及時間間隔δtij不同，所以調節限差εv大小，可以取

式中：

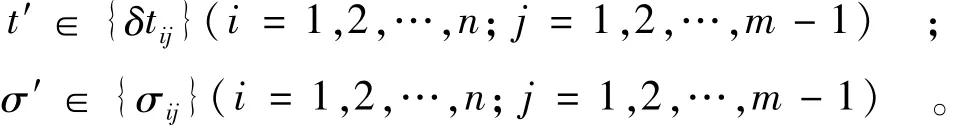
為了使調節限差的結果不至于影響所有監測點的情況，需要嚴格控制調節限差εv大小，可以取

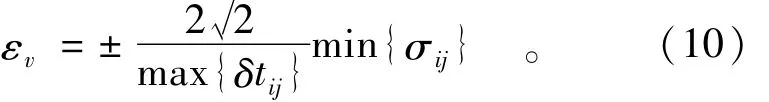
3 算例分析

3.1 事件模型的建立

結合我國某大壩為例［8］，取該變形體上某部位的16個監測點數據為例，由于觀測該監測部位的視線不得不穿過水面，致使觀測結果受水汽的影響較大，觀測數據含有大量的噪聲，如圖1所示。通過對原始觀測數據序列的擬合，計算得到16個監測點各自在x方向的觀測精度，如圖2所示。

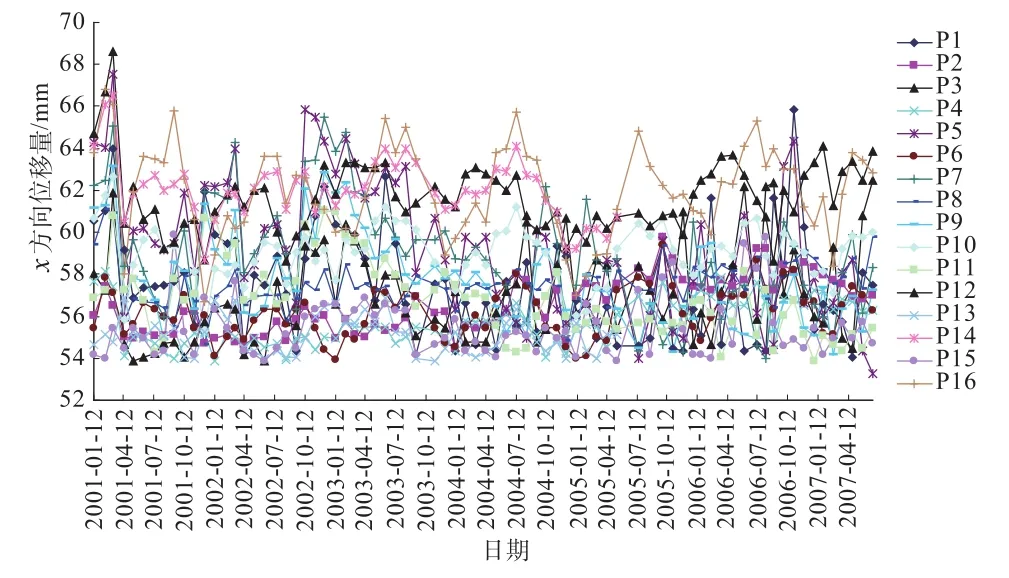
圖1 監測點位移過程線Fig.1 Process of disp lacement atmonitoring points

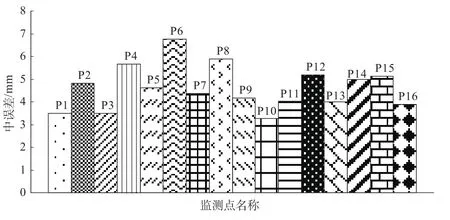
圖2 原始觀測中誤差Fig.2 Mean square errors of the original observations

根據式（2）計算得到平均位移速率閾值v0＝1.90 mm／d；由于觀測值的真誤差無法得到，故采用式（9）計算可以調整限差εv的大小。最大天數間隔為max｛δtij｝＝14 d，根據圖2，最小原始觀測中誤差min｛σij｝＝3.26 mm，根據式（10）得到εv＝±0.66 mm／d。

為了書寫及表述方便，選取監測點P3～P7這5個監測點自2003年4月11日至2004年7月11日間部分數據。位移數據及平差后各監測時刻的真誤差估計值如圖3所示。

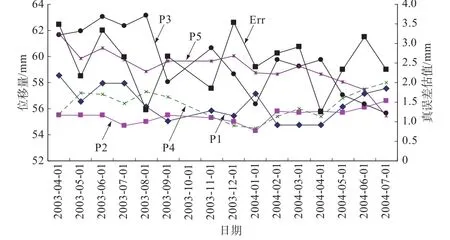
圖3 位移過程線及各時期真誤差估計值Fig.3 Displacement process and estimated true errors in each period

在沒有受到觀測誤差影響前，根據式（3）及平均位移速率閾值v0＝1.90 mm／d，得事件矩陣ME；如果考慮每個監測時刻觀測誤差的影響，顧及式（6），其事件矩陣為M′E；根據式（10），調節εv大小，本例前面計算得到εv∈［－0.66，0.66］，根據式（8）適度調整閾值v0＝1.90＋0.22＝2.12 mm／d，據此計算事件矩陣M″E，如圖4所示。

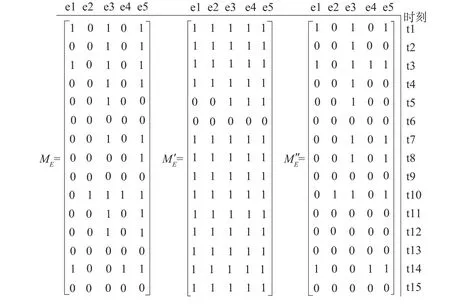
圖4 各計算結果的狀態矩陣Fig.4 Statusmatrices in three form s

比較圖4中的3個事件矩陣可以看出，由于受到原始觀測誤差的影響（如圖3中的“Err”線所示），致使事件狀態矩陣M′E與ME有較大差異，如果按照事件狀態矩陣M′E進行分析計算（如回歸分析、時間序列等），那么計算結果會受到原始誤差很大的影響；而通過“事件”模型調節εv大小，適度調整閾值v0，得到事件矩陣M″E，可以發現，事件矩陣M″E與ME僅存在少量差異，在進行Cox回歸模型計算時［6］，分析結果受原始誤差的影響將會得到有效的控制。

3.2 Cox回歸模型計算結果

仿照圖4數據變換過程，對圖1的觀測序列計算事件狀態矩陣，分別將事件狀態矩陣的3種計算結果ME，M′E和M″E代入Cox回歸模型計算［6，9］，結果如表1所示。

表1 3種不同事件矩陣的Cox回歸模型計算結果Table 1 Results calculated by Cox regression model from three different statusmatrices

從表1可以看出，由于觀測序列含有偶然誤差的影響，致使M′E矩陣代入Cox回歸模型計算得到的風險比超過ME的計算結果，而經過模型參數調節得到的M″E矩陣，其回歸模型計算結果，接近M′E矩陣的Cox模型計算結果，即調節模型參數后的事件矩陣，減弱了原始觀測數據中誤差對Cox回歸模型計算結果的影響。

結合“風險比”的解釋意義，實際上，隨著監測時間的推移，該變形體整體的位移速率呈逐步下降的趨勢，按照M′E矩陣（即受原始數據觀測誤差的影響）的計算結果，平均約遞減92.0%；按照M″E矩陣（即調節事件模型參數后）的計算結果，平均約遞減95.8%，接近以ME矩陣（即原始數據不含有觀測誤差）為準的計算結果96.5%。

4 結 語

對于變形觀測工作來講，由于受觀測條件影響（如水汽較大），致使觀測結果不可避免地受到一定影響。可以建立“事件”模型對原始數據進行轉換，把原始監測數據轉換成“事件狀態”數據，通過調節模型參數、速率閾值參數的大小，在一定程度上可以減弱觀測誤差帶給Cox加固歸模型的影響，能夠進一步提高計算結果的準確度。

［1］ BONALDIP，FANELLIM，GIUSEPPETTIG.Displacement Forecasting for Concrete Dams via Deterministic Mathematical Models［J］.InternationalWater Power andDam Construction，1977，29（9）：42－45.

［2］ FANELLIM，GIUSEPPETTIG.Techniques to Evaluate Effects of Internal Temperatures in Mass Concrete［J］.InternationalWater Power and Dam Construction，1975，（6）：162－168.

［3］ 文鴻雁，張正祿.小波分析與傅立葉變換相結合在探測周期性變形中應用［J］.測繪通報，2004，（4）：14－16.（WEN Hong-yan，ZHANG Zheng-lu.Detection of the Periodical Signal in the Deformation Analysis with Wavelet and Fourier Transformation［J］.Bulletin of Surveying and Mapping，2004，（4）：14－16.（in Chinese））

［4］ 陳 剛，趙 斌，胡友健，等.無電離層延遲組合GPS數據的小波預處理方法研究［J］.測繪學報，2009，38（6）：477－481.（CHEN Gang，ZHAO Bin，HU Youjian，et al.Research on GPS Pre-processing Method for Ionosphere-free Combination Data Using Wavelet［J］.Acta Geodaetica et Cartographica Sinica，2009，38（6）：477－481.（in Chinese））

［5］ PURER E，STEINER N.Application of Statistical Methods in Monitoring Dam Behavior［J］.InternationalWater Power and Dam Construction，1986，（12）：33－35.

［6］ COX D R.Regression Models and Life Tables（with Discussion）［J］.Journal of the Royal Statistical Society，Series B，1972，（34）：187－220.

［7］ MARUBINI E，VALSECCHIM G.Analyzing Survival Data Form Clinical Trials and Observational Studies［M］.Chichester，UK：John Wiley＆Sons，1994.

［8］ 趙 卿.大壩變形分析多測點統計模型的應用研究［D］.武漢：武漢大學，2010：92－100.（ZHAO Qing.Research and Application of the Multi-point Statistical Model on Dam-deformation Analysis［D］.Wuhan：Wuhan University，2010：92－100.（in Chinese））

［9］ 趙 卿，黃聲享.一種分析大壩整體位移變化規律的新方法［J］.武漢大學學報（信息科學版），2009，12（34）：1419－1422.（ZHAOQing，HUANG Sheng-xiang.A Way for Overall Analysis on Dam’s Displacement［J］.Geomatics and Information Science of Wuhan University，2009，12（34）：1419－1422.（in Chinese） ）

（編輯：曾小漢）

Impact of Reducing Observation Errors on Regression M odel

ZHAO Qing1，2，ZHOU Xing-dong1
（1.School of Geodesy and Geomatics，Jiangsu Normal University，Xuzhou 221116，China；2.Jiangxi Provincial Key Lab for Digital Land，Fuzhou 344000，China）

Errors of deformation monitoring data has great impact on the modeling of the data sequences.A new model called Event-Model，which changes the expression of the original observation data，was proposed.First，the deformation rate at each monitoring point in the original data was calculated，and then the rates were divided into several ranges.By converting the original observation data into events，the numerical data were divided into categorical datawhich were composed of thematrix，named EventMatrix in this paper，which could be fitted to the Cox regression model.Each group of categorical data contained certain ranges.On the basis of experiences and the actual situation such as the average displacement rate calculated previously，parameters in the“Event-Model”were adjusted to avoid or weaken the effect of observation errors.Themean square error of the observation data could be treated as adjusted parameters instead of unknown true errors in practice.The influence ofmonitoring data containing observation errors on the follow-up Cox regressionmodel can be reduced to some extent and improve the accuracy of the calculation results.

observation errors；deformation monitoring；eventmodel；Cox regression model

TV698.1

A

1001－5485（2012）12－0020－04

勘誤啟事

10.3969／j.issn.1001－5485.2012.12.005 2012，29（12）：20－23

2011－10－08；

2012－02－20

江蘇師范大學博士學位教師科研支持項目（10XLR23，10XLR16）；江西省數字國土重點實驗室開放研究基金資助項目（DLLJ201203）

趙 卿（1983－），男，江蘇徐州人，講師，博士，主要從事變形監測與災害預報的研究，（電話）18752128985（電子信箱）zhaoqing7＠QQ.com。

《長江科學院院報》2012年第10期《纖維混凝土在水利工程中的應用》一文中的作者單位：“b.流域水利河南省高校工程技術研究中心”應為“b.小流域水利河南省高校工程技術研究中心”（P114）。特此說明，并對該文作者致歉。