彈性飛機平衡的陣風外載荷計算與分析

嚴 德 楊 超 肖志鵬

(北京航空航天大學 航空科學與工程學院，北京100191)(北京民用飛機技術研究中心，北京100083)

彈性飛機的連續紊流響應是動氣動彈性問題的一個重要部分.隨著航空科學技術的不斷發展，飛機的性能要求不斷提高，比如高速度、大過載、低結構重量等，這使得飛機的柔度增大，彈性效應愈加明顯，由氣動彈性效應引起的連續紊流載荷對大型飛機翼載荷的大小和分布有較大的影響［1－2］.因此，在飛機結構設計中，就有必要考慮彈性飛機的連續紊流載荷.

20世紀50年代，在通信和電子工程領域處理隨機信號或噪聲的功率譜分析方法被引入到對飛機大氣紊流響應的研究中.隨后，將大氣紊流當作平穩隨機過程的功率譜密度(PSD，Power Spectral Density)方法得到了發展和完善，并被引入到各種載荷設計規范，從而形成了現有規范或條例(如適航條例等)中的陣風載荷設計準則［3］.依據這些準則可以得到單個載荷的設計值，比如飛機關鍵部位(翼根、發動機吊掛處、機身某個隔框處等)的內力或者某個結構單元的應力.但規范中并未指明這樣的載荷如何用于飛機的結構設計.由于忽略了載荷之間的組合特性(符號和大小)，這類單個載荷無法直接用于結構的設計與分析.其他的一些連續紊流響應分析方法也主要致力于連續紊流的模型描述和相應的計算方法［4－10］，但仍然存在上述問題.因此，連續紊流載荷在飛機設計中的應用一直存在困難，直至目前，尚沒有統一的解決方案.

針對這一問題，國外學者從外載荷、內力和應力3個層面進行了連續紊流載荷的應用研究.文獻［11］推導了2個應力之間的相關系數，并根據剪切、拉伸、壓縮安全裕度為0給出了結構單元的使用強度包線.在結構設計中，結構單元的復合應力落在使用強度包線的概率不能超過規定的值，該方法計算量較大，需要對每個結構元件進行分析.另外，對于平面應力板單元，會有沿2個方向的正應力和面內的剪應力，使用強度包線難以考慮.傳統梁應力分析法適用的對象為傳統的梁結構，直接在梁結構的各截面處對彎矩、剪力和扭矩進行組合，并假設剪力與彎矩同相(即同時取到最大值)，選取八角形的頂點為載荷設計點，根據傳統的梁結構理論進行強度分析［12］，對于較為復雜的翼面結構來講，該方法難以處理.匹配情況法是一種“工程化”的方法，其基本思路將固有振型下的外載荷分布作為基元載荷，通過基元載荷的組合，使某些位置處的載荷達到設計值，同時獲得結構其他位置處的載荷分布［13－14］，但在該方法中，未使用非定常氣動力，因此基元載荷之間的“相位”考慮不足.此外，在一些結構優化設計的研究中，對連續紊流載荷的處理也多集中在結構元件的應力上［15－16］.

另外，飛機的結構動力學模型著重于結構整體的動力學特性(質量和剛度特性)，難以獲得準確的應力響應.因此，使用動力學模型獲得外載荷分布，再用于靜力學模型的強度分析和校核是一個有效的辦法.

有鑒于此，本文考慮非定常氣動力，使用功率譜密度響應方法和載荷累加法計算結構的外載荷響應，并依據平穩隨機過程的相關性，證明并生成具有外載荷形式的平衡的連續紊流載荷分布，同時給出連續紊流載荷的設計情況，以便于飛機的結構強度分析和優化設計.

1 基本理論

1.1 連續紊流的載荷響應計算

由于von Karman紊流功率譜在高頻的漸進斜率與實際測量的結果較為一致，因此處理彈性結構的工程問題常采用von Karman紊流功率譜.頻率域的von Karman功率譜密度為連續紊流響應涉及較寬的頻率范圍，必須考慮氣動力的非定常效應.在彈性飛機的動響應問題中，常采用亞音速偶極子格網法進行頻域內的諧振蕩形式的非定常氣動力計算，減縮頻率k是其特征參數.因此，模態坐標下的頻域連續紊流響應方程［17］可寫為

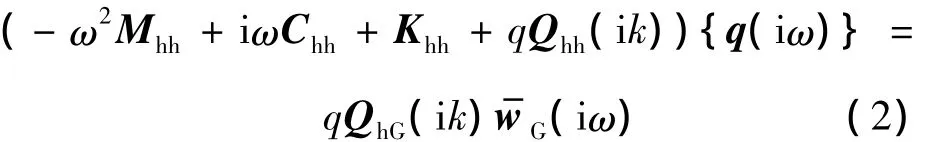
其中，下標“h”表示模態自由度;Mhh是廣義質量矩陣;Khh是廣義剛度矩陣;Chh是廣義粘性阻尼矩陣;q是動壓;q是模態廣義坐標列陣;Qhh是因彈性運動而引起的廣義非定常空氣動力矩陣;QhG是陣風下洗引起的非定常空氣動力列陣;w－G是陣風下洗.

由于本文致力于給出外載荷分布，因此使用載荷累加法計算彈性飛機結構某節點處的載荷.與其他連續紊流載荷計算方法(如模態位移法)相比，載荷累加法能更好地處理剛體運動引起的載荷.節點載荷的頻率響應為慣性力、彈性運動及陣風引起的氣動力之和［18］，其表達式如下:

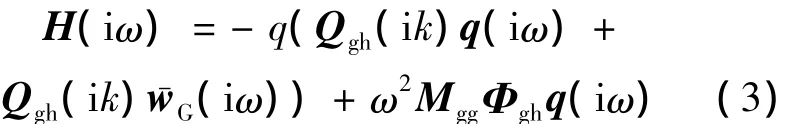
其中，下標“g”表示結構自由度;Mgg為結構的質量矩陣;Φgh為節點處的模態矩陣.

根據線性系統的隨機過程理論，基于式(3)的頻率響應函數，節點載荷的響應功率譜為

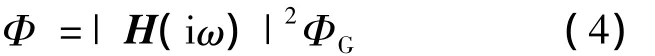
其中，ΦG為陣風功率譜密度.

通過對響應功率譜的積分，即可得到節點載荷的均方根值:

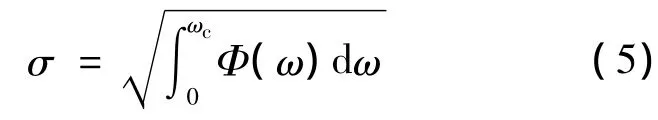
其中，ωc為計算的截止頻率.

任意2個節點 i，j處的載荷相關系數［16］為

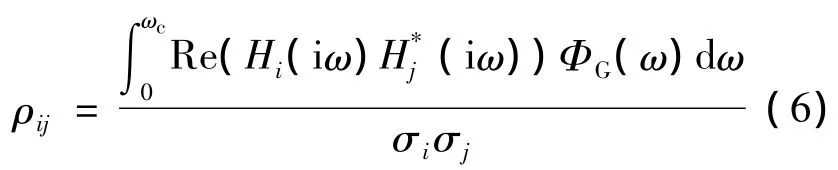
1.2 平衡的連續紊流載荷分布

對于同一個隨機連續紊流，飛機上各個節點載荷之間是相關的，這種相關性可用相關系數來衡量.根據等概率的高斯分布假設［18］，當節點 i的載荷取其均方根值時，節點j處與節點i相關的載荷為

依據式(7)，就可得到一個連續紊流的相關載荷分布.這樣的相關載荷分布考慮了每個節點載荷取其均方根值時，其他節點載荷的大小和方向，從而避免了各個節點載荷均取其均方根值的保守情況.

從式(7)出發，可以證明這組載荷分布是平衡的.將式(6)代入式(7)，并對式(7)求和，可得

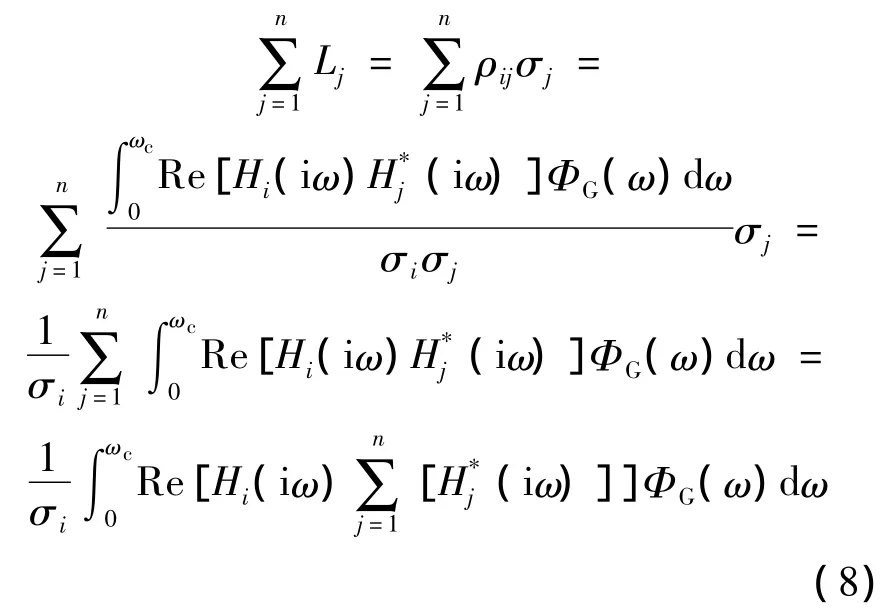
回顧式(3)，每個節點上載荷的頻率響應函數由慣性力和氣動力疊加而來.對于全機來說，在某一頻率下，所有的慣性力和氣動力之和應該是平衡的，即所有節點上載荷的頻率響應函數之和應該為0，因此

所以

式(9)表明:當某一節點載荷取其均方根值時，按相關系數匹配出的載荷分布是平衡的.這樣就把隨機的連續紊流載荷轉換成多組平衡的外載荷分布，有利于進行飛行載荷分析和結構強度設計.

2 算例

2.1 模型描述

為了獲得第1節中的連續紊流外載荷分布并驗證其平衡，本文建立了某型雙尾撐大展弦比飛機的結構動力學模型，用集中質量單元模擬飛機的結構質量、燃油質量以及裝置質量.空氣動力學模型為平板氣動力模型，飛機的展弦比為18，其結構模型和氣動力模型如圖1所示.

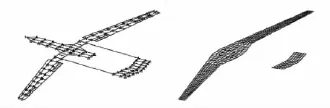
圖1 飛機的結構和氣動力模型

計算中選取了飛機的沉浮和俯仰剛體模態，以及翼面的主要彎曲、扭轉模態和機身的彎曲模態，其固有振動頻率如表1所示.由于進行的是垂向連續紊流載荷的計算和分析，因此只選擇了飛機的對稱模態.文中的紊流尺度取L=760 m，紊流速度 σG=1.0 m/s，飛行馬赫數為 0.3，高度為海平面.

表1 飛機固有振動模態

2.2 計算結果

使用第1節中的方法獲得連續紊流載荷分布，首先要得出結構上各個節點(僅包含有質量的節點和氣動力作用的節點)的外載荷響應.從節點載荷的響應功率譜能清晰地看到彈性振動對連續紊流響應的影響.

文中選擇在翼尖節點(222)、平尾節點(225)和重心處節點(226)輸出2.2.1節中的載荷響應功率譜，其中節點226還用于2.2.2節中的載荷分布示例.節點在飛機上的分布如圖2所示.圖中的坐標系226位于重心處，用于2.2.3節中的全機載荷平衡檢驗;坐標系224用于輸出2.2.4節中的載荷組合包線，位于機翼翼根.

2.2.1 載荷的響應功率譜密度

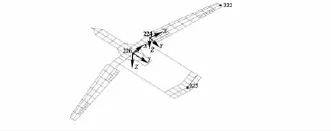
圖2 飛機的載荷輸出節點和坐標系

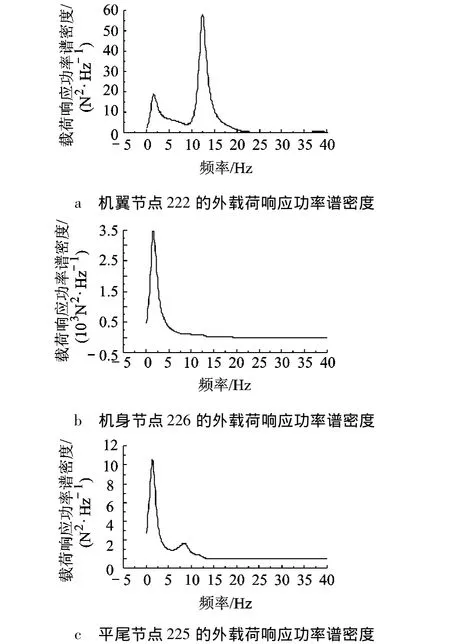
圖3 節點外載荷的響應功率譜密度

圖2所示的3個節點處的載荷響應功率譜如圖3所示.從圖3中可以看出，飛機的剛體運動模態對3個節點的載荷均有影響，尤其是機身節點226.節點222位于翼尖，其載荷功率譜的最大峰值出現在彈性振動頻率段(12.5Hz)，主要由飛機的機翼二階彎曲引起.而節點225的第2個峰值則主要由飛機的機身一階彎曲引起.機身節點226處的載荷較大，主要是由于該節點處的質量大，從而慣性力成為載荷中的主要部分.這種外載荷形式的連續紊流反映出了飛機的結構質量分布和彈性振動帶來的影響.

2.2.2 連續紊流外載荷分布

根據1.2節中的方法，得到多組載荷分布(考慮每個載荷取正和負的均方根值).每組載荷分布都對應于某個節點載荷取其均方根值，而其他節點載荷與之相關.作為示例，此處給出當節點226處取其均方根值時，機身中部的載荷分布，如圖4所示.從圖4中可以發現，載荷分布是左右對稱的.這是因為垂向連續紊流速度在飛機的兩側是對稱的，同時飛機的質量和剛度分布相對于其對稱面也是對稱的，所以載荷響應也對稱，而且對稱節點載荷之間的相關系數是1.0，不存在“相位”的差別.實際上，在垂向連續紊流作用下，任何一組載荷分布都是左右對稱的.另外，機身上的載荷較大，同樣是因為機身上質量較大.

圖4 機身中部的載荷分布

2.2.3 載荷平衡檢驗

為了驗證上述載荷分布是平衡的，文中給出了2.2節的載荷分布相對于坐標系226的全機剪力、彎矩和扭矩，如圖5所示.圖中的橫坐標表示展向站位，載荷積分從右機翼翼尖到左機翼翼尖.

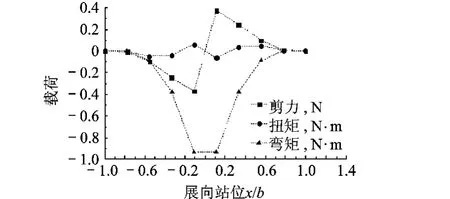
圖5 全機載荷的展向分布

由于垂向連續紊流速度的分布在飛機上左右對稱，因此飛機左右兩側的彎矩相等，且飛機對稱面上的剪力和扭矩為0，即飛機左右兩側各自的剪力以及扭矩之和為0.這種情況類似于飛機作對稱機動飛行時的載荷分布.實際上，任何一組載荷分布都具有這樣的特征.這表明按照第1節中的方法，所得到的載荷分布是全機平衡的，可以用于飛機的結構強度分析.

2.2.4 載荷包線

文中方法得到的載荷具有多組載荷分布.對于飛機的某個站位，這些載荷分布并不都是臨界載荷設計點，因此必須對各組載荷分布進行篩選.通常是將載荷組合的外緣點連接起來，形成載荷包線［19］.本文開發了針對某個站位的載荷包線計算和載荷設計點選取的程序.作為示例，此處給出了機翼翼根處(坐標系224)的載荷包線，見圖6.

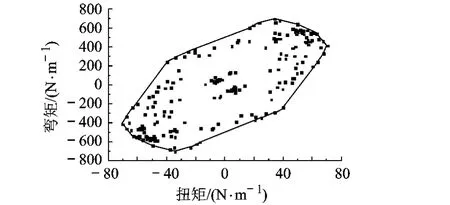
圖6 機翼翼根處的載荷包線

觀察圖6可以發現，按照本文方法得到的載荷包線關于原點是對稱的，與通常的飛行載荷包線有所不同.這可以從以下3個方面來理解:①文中的連續紊流載荷計算方法是基于飛機平衡狀態的小擾動運動方程，因此使用該方法得到的載荷是一個增量，要得到限制載荷還應附加飛機1g的平飛載荷;②文中的載荷分布考慮了每個節點取其正、負均方根值這2種情況，所以求和得到的彎矩和扭矩也勢必有對應的正值和負值;③節點載荷的等概率高斯分布假設，使得載荷包線也近似地呈現出橢圓形狀.

此外，上述載荷包線應與飛機的機動飛行載荷包線比較，從而得到飛機的載荷設計情況.

3 結論

本文基于Von Karman紊流功率譜模型和線性系統的連續紊流響應PSD方法，依據平穩隨機過程的相關性獲得了平衡的連續紊流載荷分布.通過垂向連續紊流情況下的算例計算和分析，可得出如下結論:

1)在垂向連續紊流的作用下，本文方法生成的連續紊流載荷分布是平衡的載荷分布，全機的剪力、彎矩和扭矩的展向分布說明了其平衡性，因此可用于全機的結構設計;

2)基于平衡的連續紊流外載荷分布，能夠使用機動飛行載荷中的載荷包線方法，以確定用于結構強度分析和設計的載荷設計情況;

3)外載荷形式的連續紊流載荷能夠清晰地反映出飛機結構的質量分布和彈性振動帶來的影響，適合于局部結構的連續紊流載荷響應分析和研究.

References)

［1］Bisplinghoff R L，Ashley H，Halfman R L.Aeroelasticity［M］.Cambridge，Massachusetts:Addison-Wesley Publishing Corp，1955:673

［2］陳桂彬，鄒叢青，楊超.氣動彈性設計基礎［M］.北京:北京航空航天大學出版社，2004:8－10 Chen Guibin，Zou Congqing，Yang Chao.The basis of aeroelastic design［M］.Beijing:Beihang University Press，2004:8 － 10(in Chinese)

［3］CCAR-25 中國民用航空規章第25部運輸類飛機適航標準［S］CCAR-25 Civil aviation administration of China［S］(in Chinese)

［4］Barnes T J.Overview of the activities of the AD Hoc committee of international gust specialists［R］.AGARD R-798，1995

［5］管德.氣動彈性力學手冊［M］.北京:航空工業出版社，1994:143－150 Guan De.The manual of aeroelasticity［M］.Beijing:Aviation Industry Press，1994:143 －150(in Chinese)

［6］趙繼偉，胡贊遠.民用飛機陣風載荷及減緩技術研究［J］.民用飛機設計與研究，2012(1):17－20 Zhao Jiwei，Hu Zanyuan.Research on gust load and its load alleviation technology of civil aircraft［J］.Civil Aircraft Design and Research，2012(1):17 －20(in Chinese)

［7］吳志剛，陳磊，楊超，等.彈性飛機陣風響應建模與減緩方案設計［J］.中國科學:技術科學，2011，41(3):394 －402 Wu Zhigang，Chen Lei，Yang Chao，et al.Gust response modeling and alleviation scheme design for an elastic aircraft［J］.SCI China:Tech SCI，2011，41(3):394 － 402(in Chinese)

［8］Pototzky A S，Zeiler T A.Calculating time-correlated gust loads using matched filter and random process theories［J］.Journal of Aircraft，1991，28(5):346 －352

［9］Jones J G.Statistical discrete gust method for predicting aircraft loads and dynamic response［J］.Journal of Aircraft，1989，26(4):382－392

［10］Fidkowski K J，Engelsen F，Willcox K E，et al.Stochastic Gust analysis techniques for aircraft conceptual design［R］.AIAA 2008-5848，2008

［11］Fuller J R，Richmond L D，Larkins C D，et al.Contributions to the development of a power-spectral gust design procedure for civil aircraft［R］.FAA TR FAA-ADS-54，1966

［12］Hoblit F M.Gust loads on aircraft:concepts and applications［M］.［S.l.］:AIAA Publications，1988:107 －113

［13］Stauffer W A，Hoblit F M.Dynamic gust，landing，and taxi loads determination in the design of the L-1011［J］.Journal of Aircraft，1973，10(8):459 －467

［14］Stauffer W A，Lewolt J G，Hoblit F M.Application of advanced methods to design loads determination for the L-1011 transport［J］.Journal of Aircraft，1973，10(8):449 － 458

［15］Hajela P，Bach C T.Optimum structural sizing for gust-induced response［R］.AIAA 88-2298，1988

［16］Engelsen F.Design-oriented gust stress constraints for aeroservoelastic design synthesis［D］.Washington D C:Department of Aeronautics and Astronautics，University of Washington，2001

［17］《飛機設計手冊》總編委會.飛機設計手冊第9冊［M］.北京:航空工業出版社，2002:1242－1248 Aircraft Design Manual for the General Editorial Board.The aircraft design manual book 9［M］.Beijing:Aviation Industry Press，2002:1242 －1248(in Chinese)

［18］Jonge J B，Vink W J.Gust load conditions for fatigue tests based on a continuous gust concept［R］.AIAA 97-1279，1997

［19］鄧立東，李天，薛曉春.飛機非線性飛行載荷計算方法研究［J］.航空學報，2002，23(4):317 －320 Deng Lidong，Li Tian，Xue Xiaochun.Calculation method about nonlinear flightloads of a aircraft［J］.Acta Aeronautica et Astronautica Sinica，2002，23(4):317 －320(in Chinese)