基于混沌理論在股票預(yù)測(cè)中的應(yīng)用

戴天虹，袁 博

(東北林業(yè)大學(xué)機(jī)電工程學(xué)院，哈爾濱150040)

混沌是一種低階確定性的非線性動(dòng)力系統(tǒng)所表現(xiàn)出來的非常復(fù)雜的行為，它對(duì)現(xiàn)代科學(xué)具有廣泛而深遠(yuǎn)的影響，幾乎覆蓋了一切學(xué)科領(lǐng)域，尤其是在物理學(xué)天體力學(xué)、數(shù)學(xué)、生物學(xué)、經(jīng)濟(jì)學(xué)等方面得到了廣泛的應(yīng)用［1］。我國(guó)的資本市場(chǎng)是一個(gè)具有分形維結(jié)構(gòu)的混沌系統(tǒng)［2］。對(duì)股票市場(chǎng)進(jìn)行混沌分析首先要先進(jìn)行重構(gòu)相空間。

1 相空間重構(gòu)

動(dòng)力系統(tǒng)重建稱為相空間重構(gòu)。動(dòng)力系統(tǒng)長(zhǎng)期演化中任一變量的演化過程都包含了系統(tǒng)所有變量的信息，即通過單變量時(shí)間序列反向構(gòu)造出原系統(tǒng)相空間結(jié)構(gòu)。考慮系統(tǒng)的某一單變量時(shí)間序列 {xi|i=1，2，…，N}，時(shí)間間隔選取為Δt，就可從單變量時(shí)間序列 {xi|i=1，2，…，N}分析系統(tǒng)所有變量發(fā)展演化過程，其中蘊(yùn)藏著參與該運(yùn)動(dòng)的全部變量的演化信息在相空間反向重構(gòu)得到分析。相空間重構(gòu)可從一維擴(kuò)展到多維，這樣就能充分分析動(dòng)力系統(tǒng)的所有信息。混沌系統(tǒng)有奇怪吸引子、分維數(shù)、正的Lyapunov特征指數(shù)等幾個(gè)特征量。重構(gòu)相空間就是通過選擇合適的延遲時(shí)間和嵌入維數(shù)將原系統(tǒng)重構(gòu)后，還原混沌系統(tǒng)的混沌吸引子，分析各個(gè)特征量。

Takens證明了一個(gè)合適的嵌入維，即如果延遲坐標(biāo)維數(shù)m≥2d+1，d是動(dòng)力系統(tǒng)的維數(shù)，利用原始系統(tǒng)中的某個(gè)單時(shí)間變量的延遲坐標(biāo)來重構(gòu)相空間，就可在重構(gòu)相空間里把有規(guī)律的混沌吸引子恢復(fù)出來［3］。

設(shè)動(dòng)力系統(tǒng)單時(shí)間變量x(t)，t=0，1，2，…，N，選取嵌入維數(shù)m;延遲時(shí)間τ，則m維相空間矢量:

式中:m為嵌入維數(shù);τ為延遲時(shí)間;N'=N－(m－1)τ表示m維相空間矢量的有效長(zhǎng)度。

時(shí)間序列的相空間重構(gòu)即由一維單變量時(shí)間序列重構(gòu)出一個(gè)多維多變量的確定性相空間，即可把動(dòng)力系統(tǒng)中蘊(yùn)藏著參與該運(yùn)動(dòng)的全部信息發(fā)展變化重構(gòu)出來。動(dòng)力系統(tǒng)的相空間重構(gòu)是混沌時(shí)間序列分析的基礎(chǔ)，并以此可對(duì)重構(gòu)后的相空間進(jìn)行研究。

重構(gòu)相空間目前廣泛采用的延遲坐標(biāo)狀態(tài)空間重構(gòu)法，即求取延遲時(shí)間τ和嵌入維數(shù)m之后，可按照公式 (1)對(duì)單變量時(shí)間序列進(jìn)行重構(gòu)其相空間。

本文重構(gòu)相空間采用互信息函數(shù)方法選取單變量時(shí)間序列延遲時(shí)間τ，互信息第一次達(dá)到最小時(shí)滯時(shí)作為相空間重構(gòu)的延遲時(shí)間 τ［4］。利用 CAO方法求取嵌入維數(shù) m［5］。

2 混沌特性判定

混沌系統(tǒng)其對(duì)初始條件敏感的的依賴性，使動(dòng)力系統(tǒng)中初始條件下微小的變化能帶動(dòng)整個(gè)系統(tǒng)的長(zhǎng)期的巨大連鎖反應(yīng)。，這就是蝴蝶效應(yīng)。這種局部不穩(wěn)定性和對(duì)初始值的極度敏感性，被用來判斷混沌的發(fā)生。另外，混沌吸引子通常都是非整數(shù)維的。如果序列中含有噪聲，也會(huì)存在混沌吸引子為整數(shù)維的情況。所以通過計(jì)算關(guān)聯(lián)維和最大Lyapunov指數(shù)檢驗(yàn)混沌的存在［6］。

2.1 關(guān)聯(lián)維計(jì)算

吸引子維數(shù)最常用算法為格拉斯貝格爾(Grassberger)和普羅卡恰 (Procaccia)于1983年提出的計(jì)算關(guān)聯(lián)維數(shù)計(jì)算方法，稱為G－P算法［2］。

G－P算法步驟如下:

(1)設(shè)x1，x2，…，xn為給定的一組反映系統(tǒng)狀態(tài)的單變量時(shí)間序列，采用延遲坐標(biāo)法，按照公式構(gòu)造m維相空間。

yi= (xi，xi+τ，xi+2τ，…，xi+(m－1)τ)(i=1，2，…)式中τ為延遲時(shí)間。

(2)計(jì)算該狀態(tài)空間中yi的關(guān)聯(lián)積分

式中:ε為給定的常數(shù);N是構(gòu)造矢量個(gè)數(shù)，N=n－ (m－1)p;‖yi－yi‖為yi，yj的范數(shù)，如取‖x‖=δ(x)為δ函數(shù)，δ(x)=

距離小于ε的矢量，稱為有關(guān)聯(lián)的矢量。關(guān)聯(lián)積分是關(guān)聯(lián)矢量在一切可能的N2中配對(duì)所占的比例程度。即n充分大、ε充分小時(shí)，關(guān)聯(lián)積分:

(3)對(duì)于ε的某一個(gè)適當(dāng)范圍，吸引子的維數(shù)D與關(guān)聯(lián)積分C(ε)滿足對(duì)數(shù)線性關(guān)系D(m)=ln C(ε)/lnε。

(4)重構(gòu)向空間后，即可增加狀態(tài)空間嵌入維數(shù)m，重復(fù)操作上述過程。如果單變量時(shí)間序列{xi}含有混沌吸引子，不斷增大狀態(tài)空間嵌入維數(shù)m，關(guān)聯(lián)維數(shù)Dm也會(huì)隨即增大，增長(zhǎng)率會(huì)降低。狀態(tài)空間嵌入維數(shù)m增大到一定程度時(shí)，Dm就在一定誤差范圍內(nèi)保持穩(wěn)定而不再增大，并向飽和值D收斂。由此計(jì)算出混沌吸引子的關(guān)聯(lián)維數(shù)D。如果Dm不斷增大且增長(zhǎng)率也無序變化并不收斂于一個(gè)飽和值，則該系統(tǒng)包含噪聲，是一個(gè)隨機(jī)時(shí)間序列。

2.2 最大Lyapunov指數(shù)

混沌運(yùn)動(dòng)的基本特點(diǎn)是動(dòng)力系統(tǒng)初始條件極為敏感，初始條件即使有細(xì)微的變化，動(dòng)力系統(tǒng)的狀態(tài)隨時(shí)間演變的軌線就會(huì)以指數(shù)速度分離。Lyapunov指數(shù)就是定量描述這一現(xiàn)象的量。混沌系統(tǒng)具有整體穩(wěn)定性和內(nèi)在不穩(wěn)定性。整體穩(wěn)定性使混沌系統(tǒng)的運(yùn)動(dòng)軌道收斂到混沌吸引子上。內(nèi)在不穩(wěn)定性使系統(tǒng)在收斂到吸引子上的同時(shí)，某些方向上的運(yùn)動(dòng)又是不穩(wěn)定的，導(dǎo)致系統(tǒng)對(duì)初始條件極其敏感。Lyapunov指數(shù)表示系統(tǒng)在多次迭代中平均每次迭代所引起的指數(shù)分離中的指數(shù)，是研究幾何上相鄰軌道以指數(shù)方式分離的快慢程度，反映了混沌系統(tǒng)局部范圍內(nèi)收縮與發(fā)散的速度。

對(duì)于n維動(dòng)力系統(tǒng)而言，系統(tǒng)在每一維都存在一個(gè)Lyapunov指數(shù)，表示系統(tǒng)軌道在該維上的發(fā)散程度［5］。若一個(gè)初始條件為n維的無限小橢球體的長(zhǎng)期演化過程，系統(tǒng)演化發(fā)生的局部變形使得小球體最終演化成n維橢球體，其中第i個(gè)Lyapunov指數(shù)LE可以用橢球體的第i個(gè)主軸長(zhǎng)度li(k)來定義。即:

式中，{LEi|i=1，3，……，n}按照從大到小的順序排列，稱為L(zhǎng)yapunov指數(shù)譜，并將LEi稱為最大 Lyapunov指數(shù)［6］。

如果時(shí)間序列的最大Lyapunov指數(shù)LEi大于零，就基本上可以肯定混沌的存在，最大Lyapunov指數(shù)值表明了系統(tǒng)的混沌程度［7］。

計(jì)算時(shí)間序列Lyapunov指數(shù)的方法主要分成兩種:分析法和軌道跟蹤法。軌道跟蹤法是有A.Wolf、J.B.Swift等人提出并廣泛應(yīng)用的一種方法，該算法直接從Lyapunov指數(shù)的定義出發(fā)，跟蹤系統(tǒng)的兩條軌道，從而獲取Lyapunov指數(shù)［8］。

3 數(shù)據(jù)分析

根據(jù)圖1流程圖對(duì)中國(guó)股票市場(chǎng)進(jìn)行混沌判定，并仿真預(yù)測(cè)，并由1996.2.6～2005.12.6中國(guó)股票市場(chǎng)收盤價(jià)，共2 374個(gè)點(diǎn)。最高點(diǎn):2 242.421。最低點(diǎn):520.691。

圖1 流程圖Fig.1 Flow chart

圖2 1996.2.6～2005.12.6中國(guó)股票市場(chǎng)收盤價(jià)Fig.2 Closing price of China's stock market between 1996.2.6 to2005.12.6

根據(jù)圖3所得，第一次達(dá)到最小值的時(shí)滯作為相空間重構(gòu)的時(shí)間延遲τ，即τ=13。

由圖4CAO方法計(jì)算混沌時(shí)間吸引子的嵌入維m可以看出，當(dāng)m=9的時(shí)候，Ei不再變化，即m=9。

圖3 互信息函數(shù)法確定延遲時(shí)間τFig.3 Delay timeτcalculated by mutual information method

圖4 CAO法確定嵌入維數(shù)mFig.4 Embedding dimension m computed by CAO method

由圖5和圖6可知最大Lyapounv指數(shù)數(shù)為2.342 2，飽和嵌入維數(shù) m=14，關(guān)聯(lián)維數(shù)為2.342 2。關(guān)聯(lián)維數(shù)Dm=2.342 2為非整數(shù)，最大Lyapounv指數(shù)大于0，可以斷定中國(guó)的股票市場(chǎng)是一個(gè)的混沌系統(tǒng)。收盤價(jià)最大Lyapounv指數(shù)LEi=0.078 8，因此預(yù)測(cè)時(shí)間為12.69 d。即可對(duì)股票市場(chǎng)可進(jìn)行短期預(yù)測(cè)。通過MATLAB軟件對(duì)其仿真，由圖7可以看出，收盤價(jià)和預(yù)測(cè)值之間有些許誤差。如仿真預(yù)測(cè)圖7所示。

圖5 最大Lyapounv指數(shù)Fig.5 Largest Lyapounv index

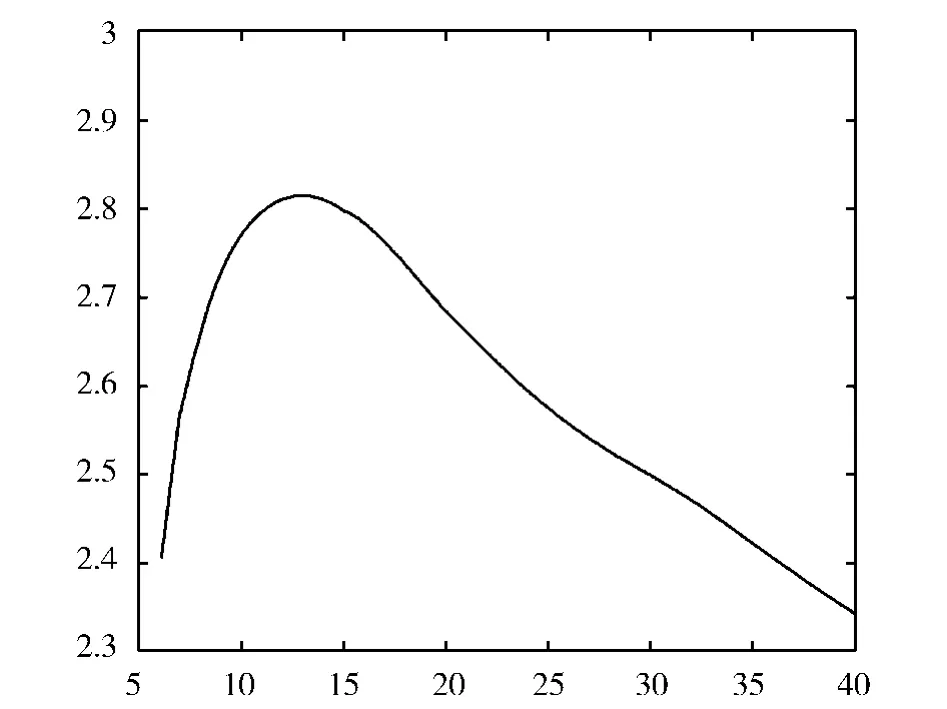
圖6 GP法求關(guān)聯(lián)維數(shù)Fig.6 Correlation dimension calculated by GP

圖7 仿真預(yù)測(cè)結(jié)果Fig.7 The results of simalation and prediction

5 結(jié)束語(yǔ)

通過相空間重構(gòu)，根據(jù)G－P算法計(jì)算的關(guān)聯(lián)維Dm非整數(shù)，通過計(jì)算得到的最大Lyapunov指數(shù)LE1均大于零，由此可以得出我國(guó)股票市場(chǎng)是一個(gè)混沌系統(tǒng)。基于最大Lyapunov指數(shù)的混沌預(yù)測(cè)證明對(duì)其可以進(jìn)行短期預(yù)測(cè)，通過MATLAB軟件對(duì)其仿真。

［1］陳 敏，徐德智，羅慶云.時(shí)間序列相空間重構(gòu)及其應(yīng)用研究［J］.計(jì)算機(jī)與信息技術(shù)，2005(11):9 －11.

［2］李建功.中國(guó)資本市場(chǎng)的混沌研究［D］.大連:東北財(cái)經(jīng)大學(xué)，2003.

［3］呂金虎，陸君安，陳士華.混沌時(shí)間序列分析及其應(yīng)用［M］.武漢:武漢大學(xué)出版社，1995.

［4］A M Fraser，H L Swinney.Independent coordinates for strange attractors from mutual information［J］.Phys Rev A，1986，33:1134 －1140.

［5］張淑清，賈 健，高 敏，等.混沌時(shí)間序列重構(gòu)相空間參數(shù)選取研究［J］.物理學(xué)報(bào)，2010，59(3):1576 －1581.

［6］金 玲，劉長(zhǎng)濱.我國(guó)建筑業(yè)增加值時(shí)間序列的混沌預(yù)測(cè)［J］.土木工程學(xué)報(bào)，2008，41(8):99 －104.

［7］王東生，曹 磊.混沌、分形及其應(yīng)用［M］.合肥:中國(guó)科學(xué)技術(shù)大學(xué)出版社，1995.

［8］王 靜，李丕仕.基于Lyapunov指數(shù)的高校圖書館圖書借閱流量混沌預(yù)測(cè)［J］.現(xiàn)代情報(bào)，2009，29(9):7 －10.