基于徑向基函數神經網絡的地下水數值模擬模型的替代模型研究

伊燕平，盧文喜，張 耘，蘆貴君，王大中，洪德法

（1.吉林省宏利水土保持咨詢有限公司，長春130033；2.吉林大學 環境與資源學院，長春130026；3.吉林省水土保持科學研究院，長春130033；4.長春市城鄉規劃設計研究院，長春130021）

理論研究和工程實踐證明，模擬優化才能解決地下水修復過程中決策方案的優選問題，因此基于數值模擬的優化模型日益受到人們的重視[1－2]。但實現模擬模型與優化模型耦合，以往運用的嵌入法、響應矩陣法、狀態轉移方程法都有自身的局限性[3]，如嵌入法，它將狀態變量（水位）和可控輸入變量（抽水量）同時作為優化模型中的決策變量，因此對于多時段的非穩定流問題，就會產生“維數災難”；響應矩陣法只適用于線性系統的模型耦合；狀態轉移方程法只適用于動態規劃。為了克服以往耦合技術方法的局限性，近年來，提出了替代模型法[4]，它在功能上逼近模擬模型，在優化模型迭代求解過程中可直接調用替代模型，大幅度地減少計算負荷，節省運算時間，是一種連接模擬模型與優化模型的有效途徑。

替代模型質量的好壞取決于采樣方法和替代模型種類的選定。替代模型種類的選取已有初步研究，Qin等運用回歸分析方法建立了雙響應面模型作為替代模型[5－6]；Johnso等應用人工神經網絡方法建立誤差逆傳播（BP）神經網絡模型作為替代模型[7－9]。本文以金泉工業園區地下水水源地為研究區，在已有研究區地下水數值模擬模型的基礎上，采用拉丁超立方抽樣方法，應用人工神經網絡方法，建立了徑向基函數神經網絡模型，作為地下水數值模擬模型的替代模型，并對替代模型的有效性進行了驗證，旨在為日后替代模型的深入研究提供科學的理論依據。

1 拉丁超立方抽樣

輸入（抽水量）—輸出（水位降深）數據集是建立替代模型的基本前提。本文應用拉丁超立方抽樣的方法，在抽水井的抽水量可行范圍內進行采樣，選取有代表性的抽水量作為地下水數值模擬模型輸入數據集（表1）。

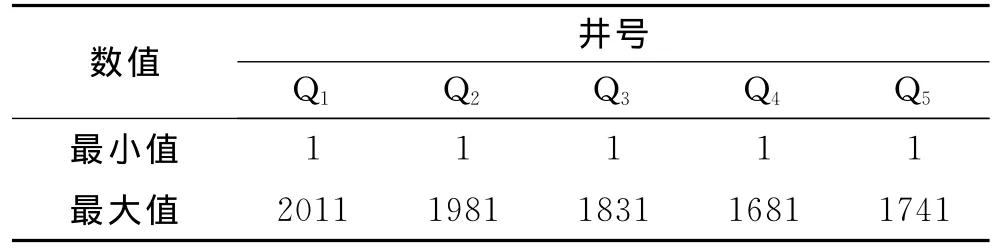
表1 實際抽水量數據資料 m3／d

1.1 基本原理

拉丁超立方抽樣（Latin Hypercube Sampling，簡稱LHS）屬于分層抽樣，是一種用采樣值反映隨機變量整體分布的方法[10]。拉丁超立方抽樣可以避免直接抽樣法數據點集中而導致的仿真循環重復問題，有效地避免了大量反復的抽樣工作[11－12]。同時，它強制抽樣過程中采樣點必須離散分布于整個抽樣空間，使得抽樣的覆蓋度得到了很好的保證，抽取的樣品具有一定代表性，如圖1所示。

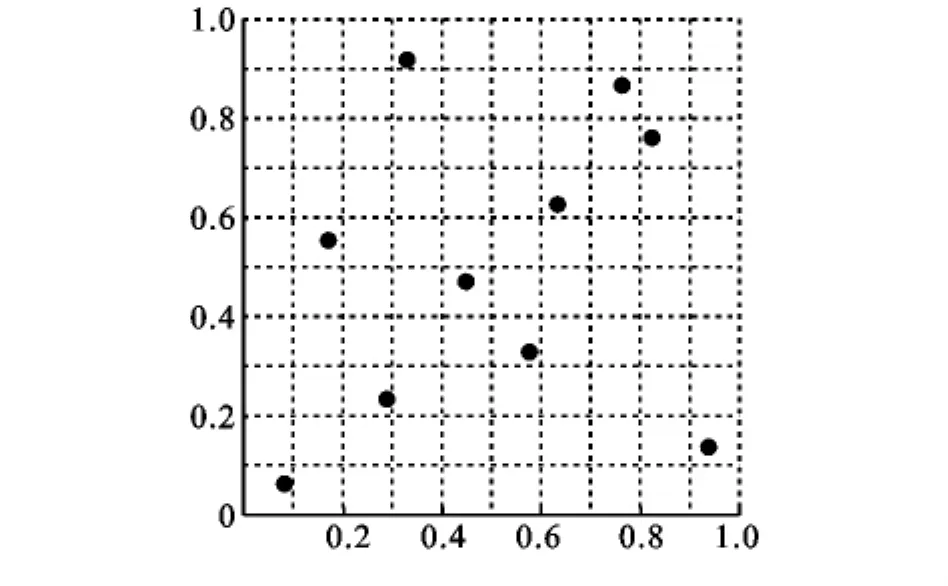
圖1 二維變量LHS抽樣示意圖

1.2 抽樣過程

1.3 抽樣結果

基于拉丁超立方抽樣的思想，確定每口抽水井的抽樣數目，H＝30。通過調用VB程序中的Randomize（）函數實現抽樣，結果見表2。

2 徑向基函數神經網絡

徑向基函數（Radial Basis Function，簡稱RBF）神經網絡是一種局部逼近的前饋式神經網絡。它由輸入層、隱含層和輸出層組成，網絡拓撲結構如圖2所示。與誤差逆傳播（Error Back—Propagation，簡稱BP）神經網絡相比，RBF神經網絡收斂速度快，能夠快速找到全局極小值。

設輸入向量為n維向量X，輸出向量為l維向量Y，則RBF網絡隱含層第i個節點的輸出為：qi＝R（PX－ciP），式中：ci是隱含層第i個節點的中心，i＝1，2，…，m，m是隱含層節點數；PX－ciP是向量X－ci的范數，代表輸入向量離開該徑向基函數中心ci的程度；R（·）為徑向基函數，它在ci處有唯一的一個最大值，隨著PX－ciP的增大，R（·）迅速衰減到零，對于給定的輸入變量，只有一小部分靠近中心的被激活。

網絡輸出層第k個節點的輸出為隱含層節點輸出的線性組合：

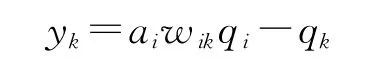
式中：wik——第i個隱含層節點到第k個輸出層節點的連接權值；qk——第k個輸出層節點的閾值。

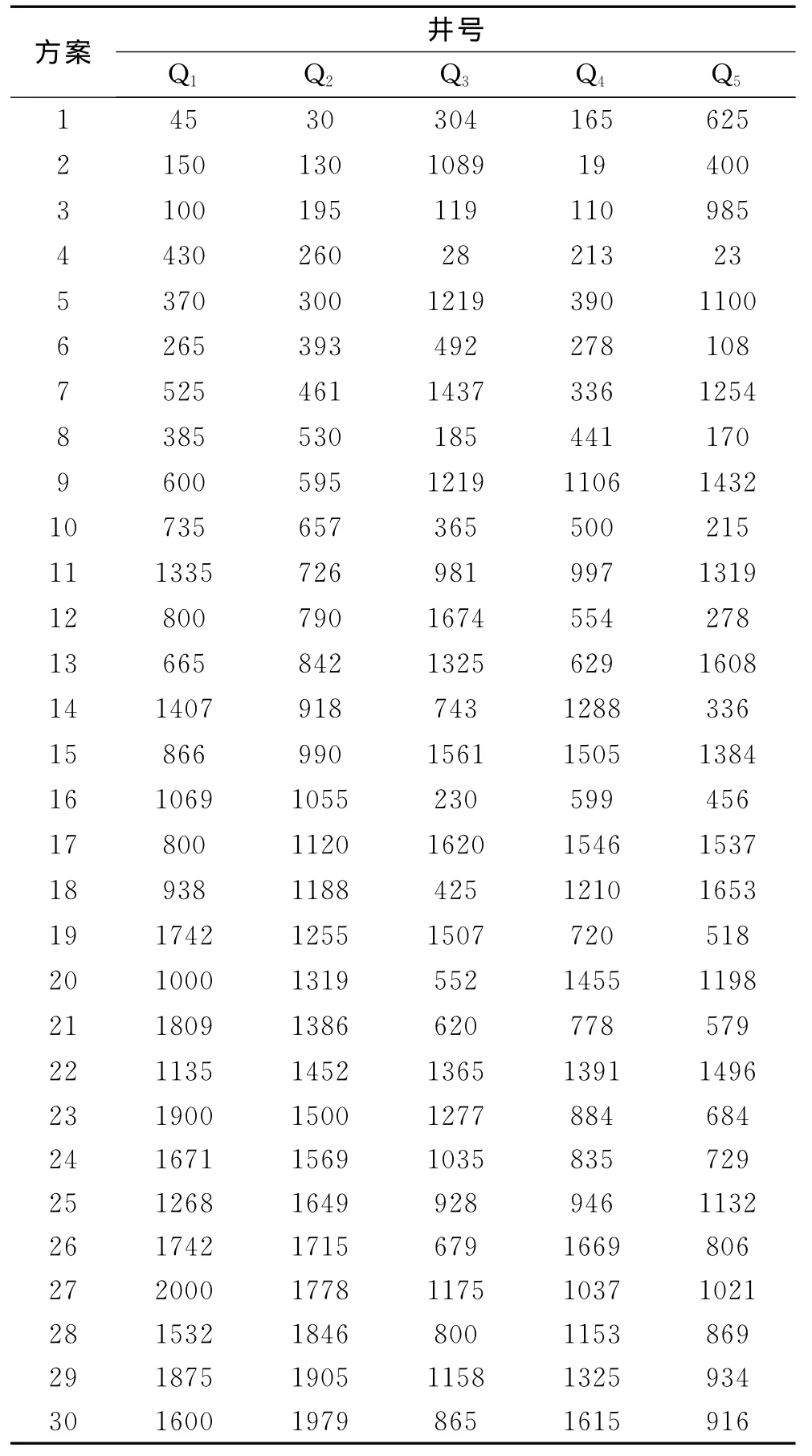
表2 LHS抽樣結果

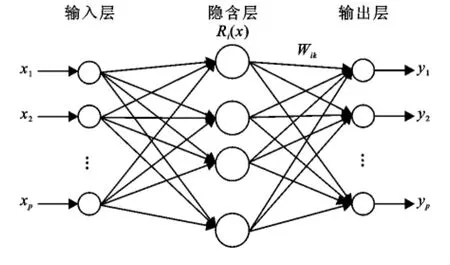
圖2 RBF神經網絡的拓撲結構

在學習階段通過用大量的樣本進行訓練，不斷修正神經網絡的各參數，使神經網絡對樣本具有模式識別能力，這樣把訓練樣本數據集輸入到RBF神經網絡中就能夠得到相應的目標輸出數據集。基于RBF神經網絡模型具有識別模式特征的能力，建立RBF神經網絡模型作為地下水數值模擬模型的近似替代模型[13－15]。

3 替代模型的建立

將抽樣得到的數據代入到地下水數值模擬模型中運行，計算得到觀測井地下水水位降深數據集，即輸出數據集。

3.1 數據處理

為了模擬計算區內5口抽水井同時抽水對地下水水位降深的影響，利用RBF神經網絡構建抽水強度與觀測井水位降深之間的非線性函數關系。將拉丁超立方抽樣得到的數據作為訓練樣本，并任意選取5組數據作為驗證替代模型有效性的測試樣本，如表3所示。

3.2 網絡的構建與訓練

利用輸入（抽水量）、輸出（降深）數據集分別建立抽水井抽水量—觀測井水位降深均值、抽水井抽水量—觀測井水位降深剩余標準差兩個RBF神經網路模型。以Matlab 6.5為平臺，調用newrb（）函數構建RBF神經網絡模型。首先建立抽水井抽水量—觀測井水位降深均值的RBF神經網絡模型。輸入層代表抽水井的抽水量，神經元個數與抽水井數目一致，定為5；輸出層表示觀測井水位降深均值，神經元個數定為1。通過運行計算機程序，得到RBF神經網絡模型的水位降深均值與模擬模型擬合的誤差。同理，構建抽水井抽水量—觀測井水位降深剩余標準差的RBF神經網絡模型，輸出層表示觀測井水位降深剩余標準差，神經元個數定為1。通過調用Matlab程序，得出RBF神經網絡模型的水位降深剩余標準差及與模擬模型結果擬合的誤差。

3.3 替代有效性驗證

RBF神經網路模型的輸出結果與地下水數值模擬模型計算得到的數據擬合效果較好。為了檢驗RBF神經網絡模型是否能夠替代地下水數值模擬模型，將RBF神經網絡模型輸出的水位降深均值和水位降深剩余標準差，分別與地下水數值模擬模型得到的結果進行誤差擬合計算，如表4所示。

經驗證，RBF神經網絡模型計算得到的水位降深均值與模擬模型計算結果擬合的平均相對誤差為0.038；水位降深剩余標準差與模擬模型計算結果擬合的平均相對誤差為0.042。擬合誤差較小，說明RBF神經網絡模型在功能上逼近模擬模型，能夠有效地替代地下水數值模擬模型。

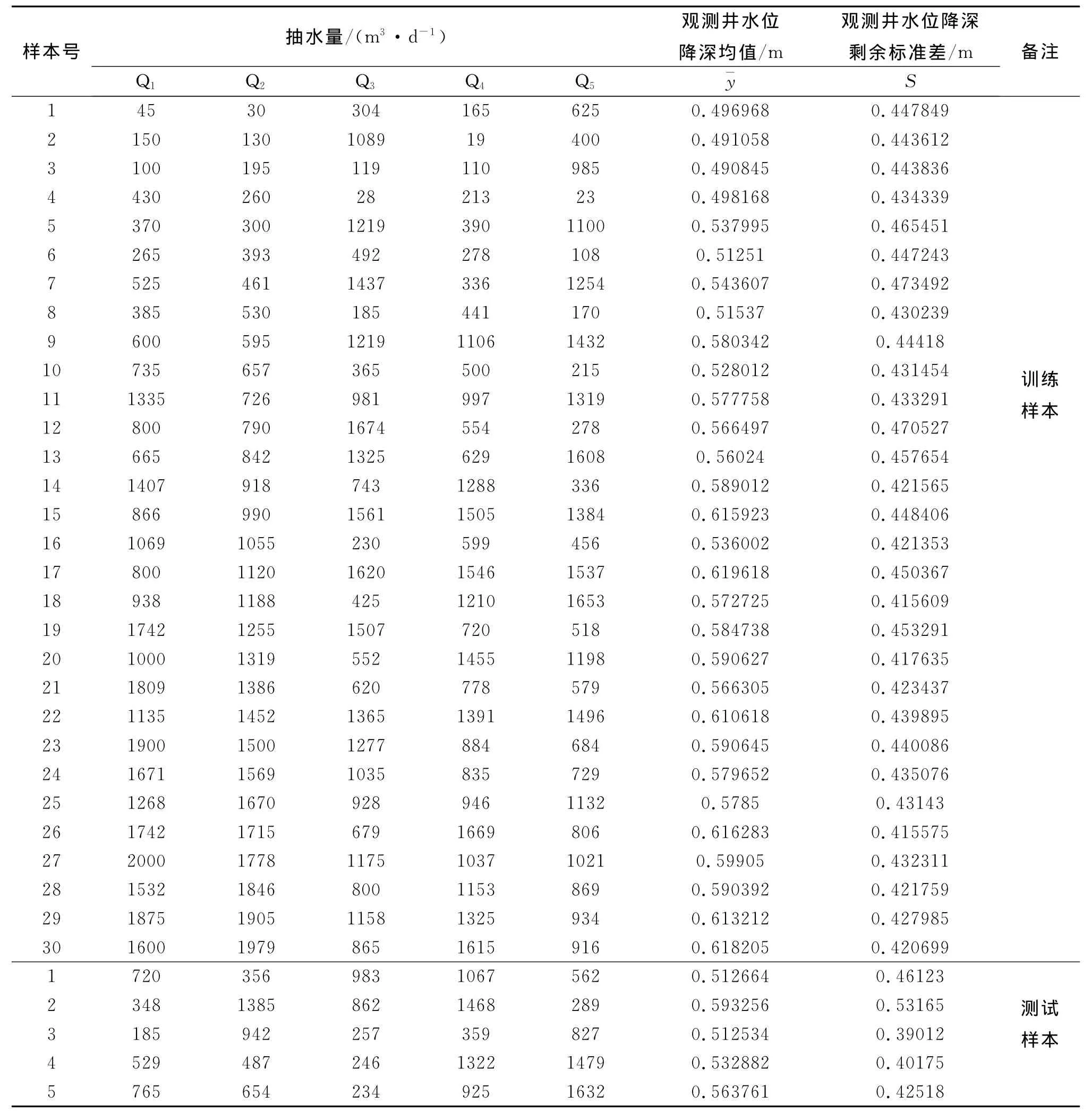
表3 RBF神經網絡訓練樣本與測試樣本數據

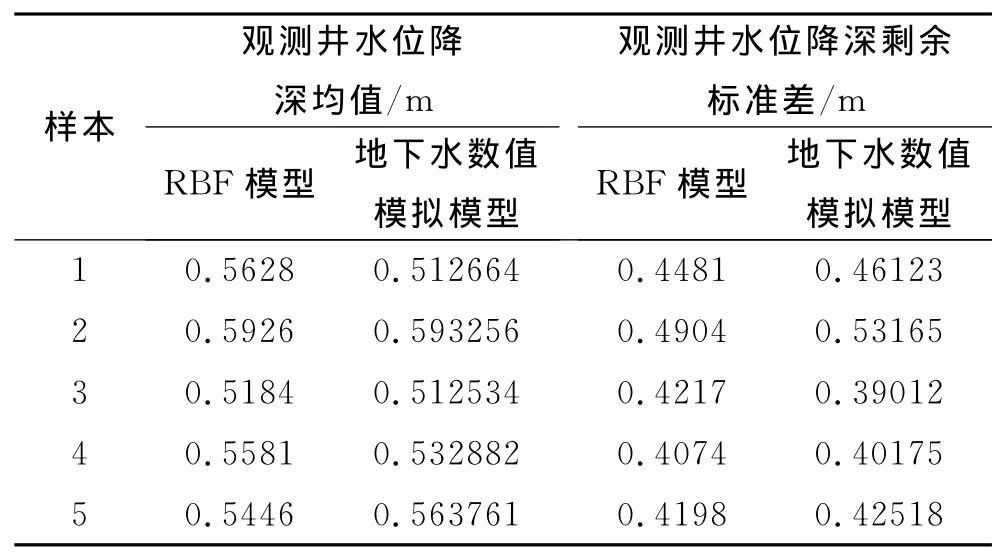
表4 RBF模型輸出結果與地下水數值模擬模型的平均相對擬合誤差

4 結論

結合地下水數值模擬模型，采用拉丁超立方抽樣，獲取建立替代模型所需的輸入輸出數據集，應用人工神經網絡的方法，構建了RBF神經網絡模型作為地下水數值模擬模型的替代模型。經驗證，RBF神經網絡模型輸出的結果與模擬模型的計算結果擬合誤差較小，表明RBF神經網絡模型在功能上逼近模擬模型，能夠有效地替代地下水數值模擬模型，可以在優化模型迭代求解過程中直接調用替代模型解決多目標優化問題。

替代模型法能夠克服以往耦合技術方法存在的局限性，大幅度地減少優化模型求解計算過程中直接調用模擬模型所造成的計算負荷，節省大量時間，是一種具有挖掘潛力和實用價值的解決問題的途徑。但本文只驗證了RBF神經網絡模型本身的替代有效性，并未對模擬優化迭代求解過程中替代模型的實用性進行驗證，因此建議將RBF神經網絡模型應用到實際中，繼續檢驗其作為替代模型的適用性，進一步完善替代模型理論，提高替代模型的準確性。

[1]He L，Huang G H，Lu H W.A stochastic optimization model under modeling uncertainty and parameter certainty for groundwater remediation design－Part 1：model development[J].Journal of Hazardous Materials，2010，176（1／3）：521－526.

[2]Qin X S，Huang G H，He L.Simulation and optimization technologies for petroleum waste management and remediation process control[J].Journal of Environmental Management，2009，90（1）：54－76.

[3]盧文喜.地下水系統的模擬預測和優化管理[M].北京：科學出版社，1999.

[4]Qin X S，Huang G H，Chakma A，et al.Simulationbased process optimization for surfactant－enhanced aquifer remediation at heterogeneous DNAPL－contaminated sites[J].Science of the Total Environment，2007，381（1／3）：17－37.

[5]He L，Huang G H，Lu H W，et al.Optimization of surfactant－enhanced aquifer remediation for a laboratory BTEX system under parameter uncertainty[J].Environmental Science＆Technology，2008，42（6）：2009－2014.

[6]Qin X S，Huang G H，Chakma A，et al.Simulation－based process optimization for surfactant－enhanced aquifer remediation at heterogeneous DNAPL－contaminated sites[J].Science of the Total Environment，2007，381（1／3）：17－37.

[7]Johnson V M，Rogers L L.Accuracy of neural network approximators in simulation－optimization[J].Journal of Water Resources Planning and Management（ASCE），2000，126（2）：48－56.

[8]Yan S Q，Minsker B.Optimal groundwater remediation design using an adaptive neural network genetic algorithm[J].Water Resources Research，2006，42（5）：407－420.

[9]薛禹群.地下水動力學[M].北京：地質出版社，1997.

[10]McKay M D，Beckman R J，Conover W J.A comparison of three methods for selecting values of input variables in the analysis of output from acomputer code[J].Technometrics，1979，21（2）：39－245.

[11]熊學玉，顧煒.基于改進LHS方法的預應力混凝土結構長期性能概率分析[J].工程力學，2010，27（4）：163－168.

[12]吳振君，王水林，葛修潤.LHS方法在邊坡可靠度分析中的應用[J].巖土力學，31（4）：1047－1054.

[13]Asim R，Sandeep G，Raymond M.A neural－network learning theory and a polynomial time RBF algorithm[J].IEEE Transactionson Neural Network，1997，18（6）：1301－1313.

[14]Lin Faajeng，Wai Rongjong，Duan Rouyong.Fuzzy neural networks for identification and control of ultrasonic motor drive with LLCC resonant technique[J].IEEE Transactions on Industrial Electronics，1999，46（5）：999－1011.

[15]王洪斌，楊香蘭，王洪瑞.一種改進的RBF神經網絡學習算法[J].系統工程與電子技術，2002，24（6）：103－105.