多節點加載預應力錨索格構梁室內模型試驗研究

劉晶晶，趙其華，張文居，3，彭盛恩，周 勇，于 宇

（1.核工業西南勘察設計研究院有限公司，成都610061；2.成都理工大學 地質災害防治與地質環境保護國家重點實驗室，成都610059；3.四川廣甘高速公路有限責任公司，成都610041）

在預應力錨索格構梁的力學計算模型中，主要研究的是錨索格梁與其下巖土體（即地基）的相互作用，因此，預應力錨索格梁的力學模型主要由其下巖土體的地基模型所決定。目前計算格構梁的力學模型中，對格構梁和周圍巖土的作用多采用彈性地基梁法進行計算，在彈性地基梁模型中，將格構梁視為地基上的梁。不同的彈性地基梁模型，主要區別在于地基模型的選取不同。對于邊坡上的格構梁，受坡角和錨索傾角的影響，梁底面摩擦力的存在使得格構梁受力變得復雜，此時選取正確的、合理的地基模型便顯得尤為重要。本文在前期的單節點加載預應力錨索格構梁模型試驗[1]的基礎上進行了多節點加載模型試驗研究，并與理論計算進行對比分析，找出更為符合實際、適合工程應用的格構梁計算方法。

1 多節點加載模型試驗

1.1 模型格構梁的選用

本次試驗模型格構梁縱梁、橫梁截面尺寸均選用1.6m×60mm×80mm，跨距600mm，懸臂長200 mm（見圖1），模型材料的選取、制作過程及其與原型的相似性等參見文獻[1－2]，此處不做過多闡述，模型橫剖面見圖2。

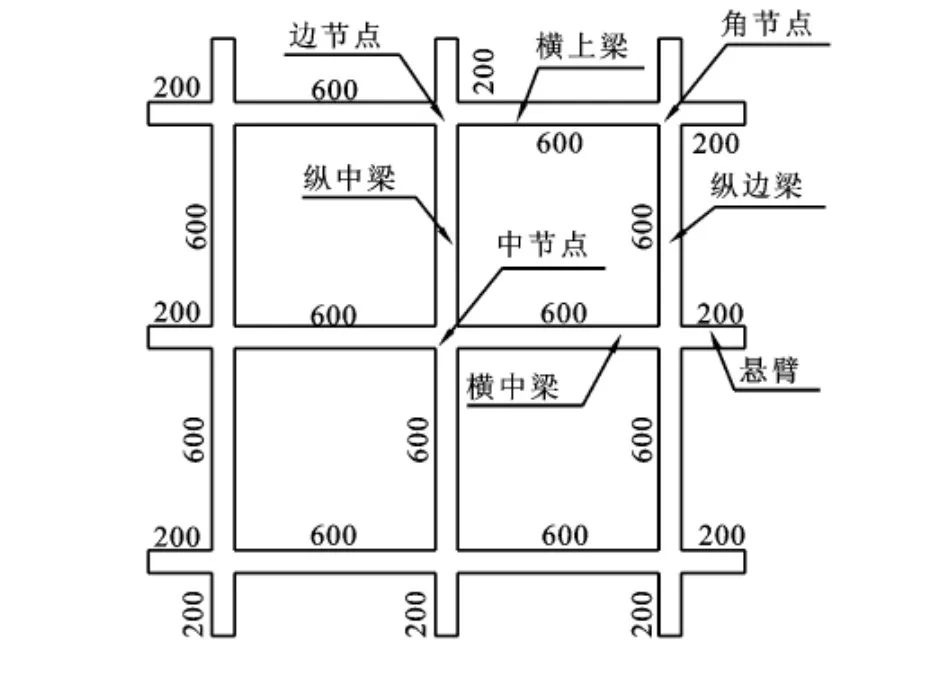
圖1 模型格構梁示意圖（單位：mm）

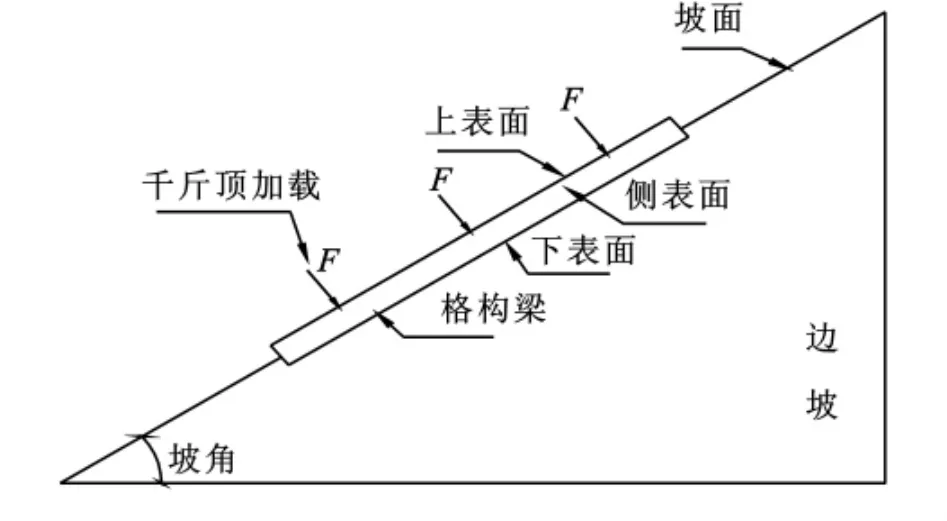
圖2 模型橫剖面示意圖

1.2 應變片的布置

格構梁上、下表面沿著梁跨的方向將應變片粘貼在中軸線上，可測得上下表面的拉、壓應變；側表面應變片的粘貼與中軸線成45°，用來測量由扭矩引起的剪應變，通過測得的應變來計算格梁彎矩及剪力。根據所要研究的具體內容以及加載方式，在格構梁右上角1／4框架內布置應變片，具體布置如圖3所示。

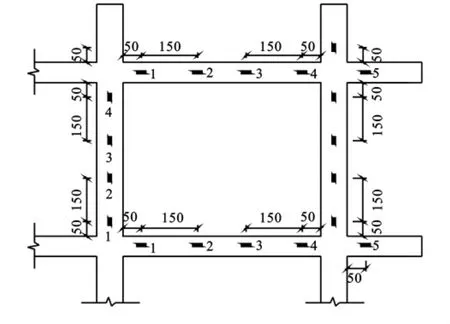
圖3 應變片布置圖

1.3 加載方式

本次試驗采用多節點加載模型格構梁來模擬實際工程中的預應力錨索格構梁，預應力方向與坡面法向的夾角為25°，以模擬錨索傾角，分兩級加載，各級加載荷載值為0.1MPa。

1.4 測試結果分析

由于橫梁摩擦力沿梁寬方向分布，因此摩擦力對其內力影響較小，因此，本節只對縱梁測試結果進行分析。根據測試結果計算出來的縱梁彎矩、剪力見表1。

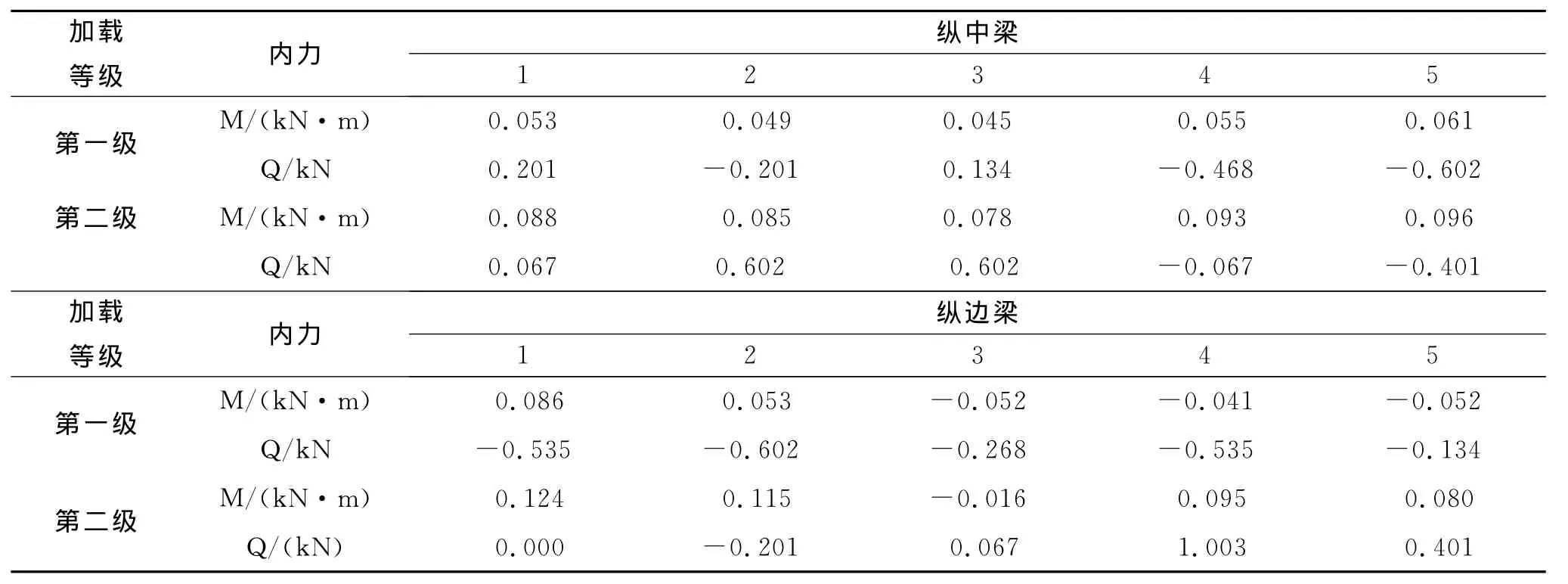
表1 格構梁內力計算結果

從表1中的數值可以看出，縱梁彎矩在跨中處以及荷載作用處較大，隨著外荷載值的增大，在跨中處很有可能出現最大負彎矩，由此可以推測格梁的危險截面有可能是在跨中或加載節點處；格構梁跨中和懸臂處剪力較大，在實際工程中進行配筋時在此兩處可適當增大箍筋間距。

2 理論計算方法

2.1 主要的地基模型

彈性地基梁主要的地基模型有以下幾種[3]：文克爾地基模型、利夫金模型、彈性半無限地基模型、有限壓縮層地基模型、雙參數地基模型、非線性模型等，這些模型大多與實際地基條件出入較大，存在很多不確定因素，計算繁瑣，并不適合工程設計人員實際運用。

2.2 考慮摩擦的Winkler彈性地基梁法

Winkler地基模型實質上是將地基看作無數分割開的小土柱，表現為一根根彈簧組成的一系列各自獨立的彈簧體系。然而，當存在水平作用力時，地基梁可能由受彎狀態轉變為偏心受壓狀態，對地基梁的配筋設計影響很大。尤其是當地基比較堅硬且地基與梁的接觸較為粗糙時，地基與梁之間的水平摩阻力的存在是明顯的，此時就有必要考慮地基與梁之間的水平摩阻力的影響。

2.2.1 微分方程的建立 考慮摩擦的Winkler地基被視為具有豎向和水平反力的彈性支撐體，地基的豎向反力仍采用Winkler地基假設，即豎向反力與該點的沉陷成正比[4－5]，水平反力假設與梁底同地基之間的相對水平位移成正比，即地基的豎向反力qv和水平反力qu可表示為：

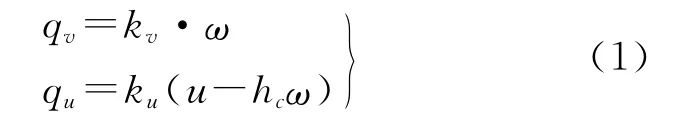
式中：kv，ku——地基豎向和水平向的反應模量，通過對模型坡體進行壓縮試驗測定；w，u——梁的撓度和截面水平位移；hc——梁中性軸到梁底的距離。

從dx一段梁的外力平衡條件，可得到梁的內力——彎矩M、剪力Q、軸向力N的關系式：

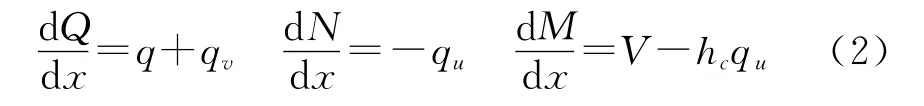
由方程（2）消去梁的內力，得到如下微分方程組：

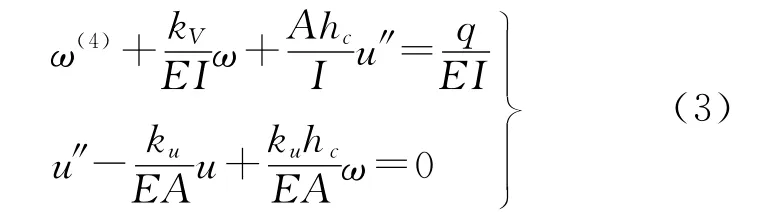
式中，E，I和A分別為梁的彈性模量（通過混凝土應力應變曲線試驗測定）、慣性矩和截面面積。

2.2.2 計算結果 現針對本次模型試驗，考慮摩擦力對格梁的縱梁影響（橫梁受摩擦力影響較小，故不予考慮），理論計算在多節點加載條件下縱梁的最大撓度ωm、最大彎矩Mm、最大軸向力Nm和地基最大摩阻應力Zm，計算結果見表2。

表2 ωm，Mm，Nm和Zm計算結果

從表2中可以明顯看出縱邊梁的變形和內力計算結果明顯大于縱中梁，其中縱邊梁的最大撓度ωm和最大彎矩要大于縱中梁27%～28%，而最大軸力和最大摩阻應力的差值則達到了74%和88%，產生該差異的原因是由于縱邊梁只受到左側三根橫梁的制約，而右側的懸臂由于長度較小，其對縱邊梁變形的約束完全可以忽略，而縱中梁左右均受到橫梁的制約，因此變形較邊梁小，由此亦可以看出在實際工程中整片格梁在坡腳、坡頂以及兩側邊界處的邊梁其變形及內力都要遠遠大于中間部分的格梁，在進行格梁內力計算時要分開考慮。

分析最大摩阻應力計算結果可以看出，當將其換算成總的摩擦力時，該值較大，且由于縱邊梁和縱中梁在最大摩阻應力上的差異達到了88%，比在撓度和彎矩上的差異大了3倍多，因此說明平行坡面的摩擦力對不同位置處的格梁變形的影響較大，因此在實際計算時不可忽略。

3 試驗結果與理論計算的對比分析

通過上述分析，可知縱梁受摩擦力影響較大，現對縱梁的最大彎矩進行對比分析，縱中梁、縱邊梁根據實測結果計算的最大彎矩與理論計算最大彎矩見表3。

表3 縱中梁、縱邊梁最大彎矩對比 kN·mm

從表3中可以看出，實測最大彎矩同理論計算值總體上相差不大，說明考慮摩擦的Winkler地基梁計算方法較為合理，但理論計算值要略小于實測值，分析其原因是由于錨索作用力的相互疊加效應，使得縱中梁和縱邊梁的彎矩值較理論計算值大出3.7%和7.7%，此外從該數值上可以看出縱邊梁的差距要比縱中梁大出一倍左右，由此可以看出邊梁的內力以及變形受外界條件影響較大，因此在進行格梁設計計算時要充分考慮到此點。

4 結論

（1）由于坡角及錨索傾角的存在，邊坡上的預應力錨索格構梁受到底面摩擦力的影響，其受力狀態變得復雜，因此在選取地基模型的時候有必要考慮平行坡面的力的作用；

（2）通過理論計算得出的梁底面的摩擦力較大，且其對不同位置處的格梁變形的影響較大，由此可以看出在進行邊坡上格構梁設計計算時，對其梁底部的摩擦力不可忽略；

（3）對比試驗測試結果與采用考慮摩擦的Winkler地基模型進行的理論計算結果，可以看出兩者相差不大，說明了考慮摩擦的Winkler地基梁的計算方法較為合理，它能更好地反映地基梁的受力特性。

[1]馬迎娟.預應力錨索格構梁復合結構的模型試驗研究[D].成都：成都理工大學，2005.

[2]劉晶晶.多節點加載預應力錨索格構梁模型試驗研究[D].成都：成都理工大學，2006.

[3]王龍，朱彥鵬，李慶福.彈性地基梁設計方法比較與分析[J].甘肅科技，2002，18（1）：39－40.

[4]周繼凱，杜欽慶.考慮水平力作用的改進型Winkler地基模型[J].河海大學學報：自然科學版，2004，32（6）：669－673.

[5]談至明.具有水平摩阻力的彈性地基上梁的解[J].力學與實踐，1997，19（3）：33－35.