傳導冷卻電流引線熱分析

昌 錕 趙保志 雷沅忠 謝秀娟

1 引言

電流引線是超導磁體系統(tǒng)中連接室溫電源和超導磁體的關鍵通流部件。電流引線常常是超導磁體系統(tǒng)的主要漏熱源，在大型超導磁體系統(tǒng)中，電流引線漏熱占磁體總漏熱的比例甚至達到50%［1］。為保證超導磁體系統(tǒng)穩(wěn)定運行，需盡量減小通過電流引線向磁體的漏熱，本文擬通過對傳導冷卻電流引線進行熱分析計算，研究減小漏熱的電流引線優(yōu)化途徑。

2 電流引線傳熱模型

電流引線軸向溫度梯度遠大于徑向溫度梯度，對于傳導冷卻電流引線可忽略輻射漏熱和殘余氣體分子導熱的影響［2］，則熱傳遞只與引線長度方向相關，進而可采用一維傳熱模型來進行分析。

電流引線可由常規(guī)材料(銅或銅合金)制作，也可采用常規(guī)材料與高溫超導材料分段制成組合引線，但傳熱分析計算均可用一維理論來分析，具體計算時可采用分段方法進行分析計算，只需對各段邊界條件進行調整。典型的傳導冷卻電流引線可由制冷機冷卻［3-4］，其一維傳熱模型可參見圖1所示。為便于分析，現(xiàn)取銅引線部分進行傳熱分析(見圖2)。

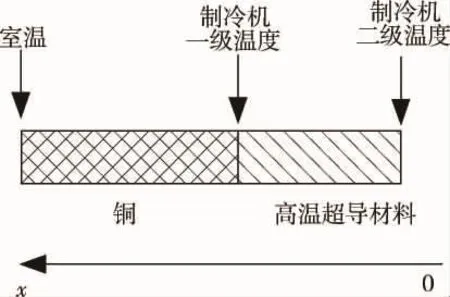
圖1 電流引線傳熱模型Fig.1 Heat transfer model of current lead

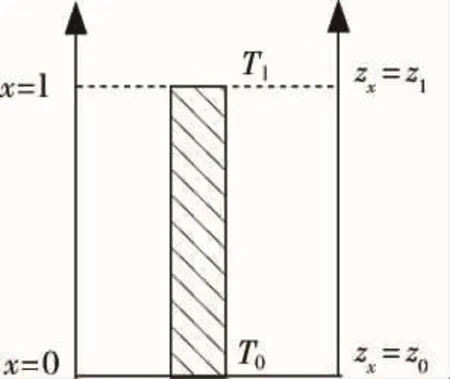
圖2 銅引線部分示意圖Fig.2 Schematic diagram of copper current lead

依據一維傳熱模型可得熱平衡方程:

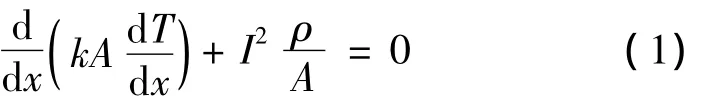
式中:ρ為電阻率Ω·m;k為熱導率，W/m·K;A為電流引線截面積，m2;T為溫度，K;I為流過電流引線的電流強度，A。為解此方程，作如下變換:

代入式(1)中得:

假定材料的熱導率和電阻率符合威德曼—弗朗茲(Wiedemann-Franz)定律，即材料的熱導率和電阻率互為倒數(shù):ρk=L0T，L0=2.45×10-8W·Ω/K2稱為洛侖茲常數(shù)［5］。則式(3)可得:

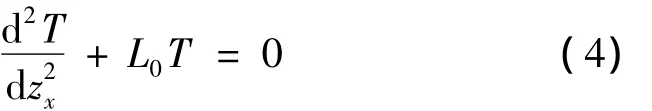
通過求解式(4)可得電流引線上的溫度分布關系式及引線兩端的傳熱關系式。

(1)溫度分布

式(4)中的特征方程為:r2+L0=0

則方程的解為:

如圖2所示，設定銅引線的長度為l，對應長度l處的溫度用Tl表示，其對應的邊界條件為:

代入方程中可得:

則引線上溫度分布為:

(2)傳熱量

引線上的傳熱量可由式(7)計算

將所得的溫度分布關系式(6)代入得:

則對引線底部zx=z0=0有:

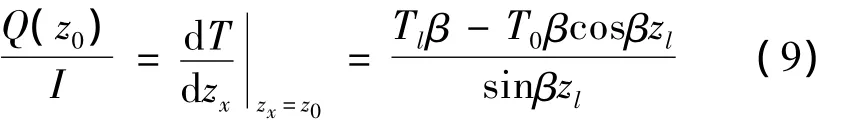
對引線的上部，zx=zl有:

3 電流引線優(yōu)化

對電流引線進行優(yōu)化設計是減小外界向磁體漏熱的有效途徑。如圖2所示，引線底部(x=0，或zx=z0=0)對應的傳熱量即為向磁體流入的熱量。對電流引線進行優(yōu)化，要求從引線流入磁體方向的熱量最小，即要求Q(z0)取最小值，由式(9)得電流引線的優(yōu)化參數(shù)zl滿足如下關系:

將式(9)代入式(11)得:

則可得:

由式(12)對應的可得:

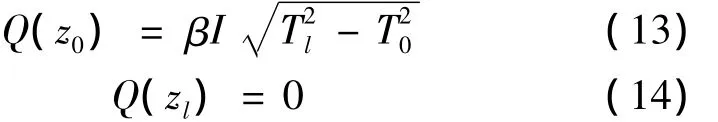
若其它條件已知，由式(12)可導出zl的優(yōu)化值，進一步利用式(2)可得到電流引線結構尺寸的參數(shù)關系。式(13)和式(14)表明，當電流引線溫度較低端的漏熱最小時，電流引線溫度較高端無熱量傳遞，此處不存在溫度梯度。

4 電流引線漏熱分析

4.1 zl取最佳值

由上可知優(yōu)化參數(shù)zl包含了電流引線的材料熱導率，通電電流，引線的長度及截面積因素，現(xiàn)將其作為綜合參數(shù)進行分析。

當zl均取最佳值時，由式(13)所示最小傳熱量中可得，電流引線溫度較低端的傳熱量與電流引線兩端的溫度及通過的電流相關。當通電電流不同時，作為實例，取T0=80 K，通電電流分別為 I=50，100，200 A，Q(z0)隨 Tl的變化規(guī)律見圖3所示。

圖中曲線表明:

(1)除Tl與T0接近區(qū)域，隨著Tl降低，Q(z0)也降低，且Q(z0)與Tl基本呈線性關系，表明降低Tl可降低電流引線低溫端的換熱Q(z0)。

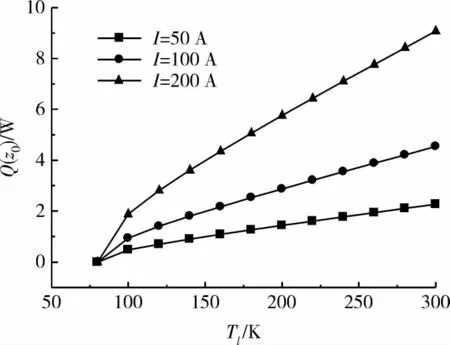
圖3 通電電流不同時Q(z0)與Tl的關系Fig.3 Relation of Q(z0)and Tl for different current

(2)Tl相同時，電流引線通過的電流越大，引線溫度較低端的換熱Q(z0)越大，且Q(z0)隨Tl的變化越大。表明電流越大，通過降低Tl可以更顯著的降低電流引線低溫端的換熱量。

當T0不同時，設定通電電流為I=100 A，分別取T0=40，60，80 K，Q(z0)隨 Tl的變化規(guī)律見圖4 所示。

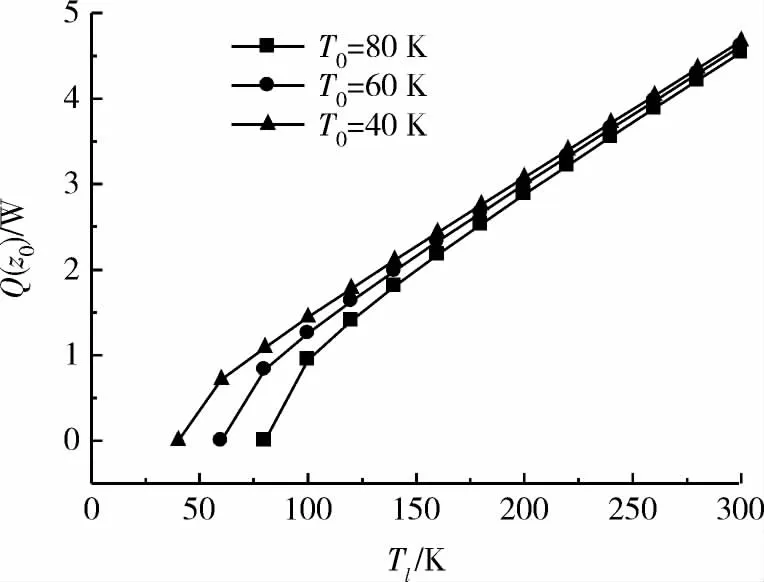
圖4 T0不同時Q(z0)與Tl的關系Fig.4 Relation of Q(z0)and Tl for different T0

據圖中曲線可得:除Tl與T0接近的情況，Q(z0)隨Tl降低而降低，且Q(z0)與Tl基本呈線性關系。相同條件下，T0越低，Q(z0)越大，即引線溫度較低端的漏熱量越大。T0越高，曲線的斜率越大，表明電流引線溫度較低端的溫度越高，降低Tl可更顯著的降低電流引線低溫端的換熱量。

4.2 zl偏離最佳值

當電流引線參數(shù)zl偏離最佳時，相應Q(z0)將增大，下面通過實例分析zl偏離最佳值時，對應Q(z0)的變化特點。

設定 Tl=300 K，T0=80 K，I=100 A，則對應漏熱最小時zl的優(yōu)化值可由式(12)導得zl=8 285.755 A·K/W。若將zl分別以10%遞增和遞減(以z'l表示)，則漏熱增大，由式(9)可得Q(z0)，相應變化曲線見圖5所示。

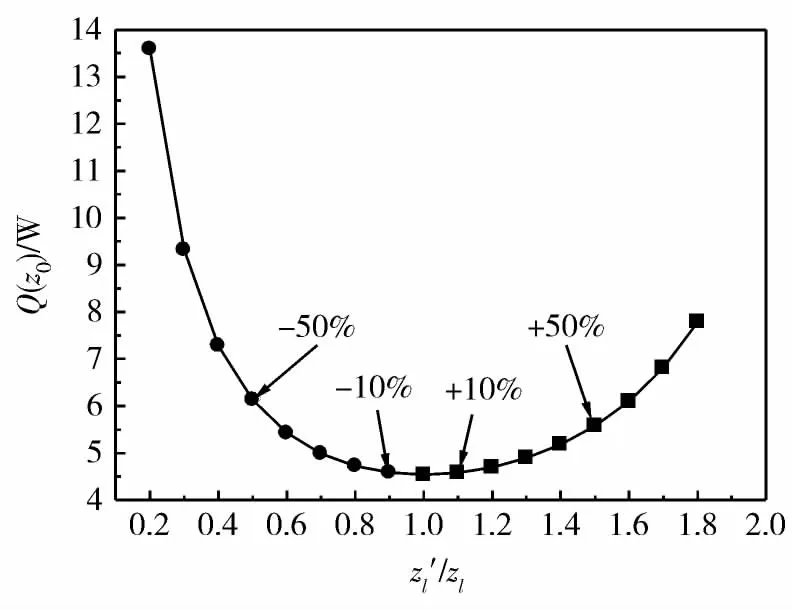
圖5 zl偏離最佳時，Q(z0)的變化情況Fig.5 Variation of Q(z0)with z'l/zl

由圖可得:

(1)zl增加和減小相同百分比，zl減小時對應的Q(z0)值大于zl增加時對應的Q(z0)值，且zl同時增加和減小的數(shù)值越大，對應的Q(z0)相差越大，表明增加zl比減小zl更有利于降低通過電流引線的漏熱量。

(2)當zl偏差較小，如本實例中增加或減小10%時，對應Q(z0)變化很小，幾乎可以忽略不計。當偏差較大時，對應Q(z0)差別較明顯，依據圖中數(shù)據有:當zl取最佳值時，即z'l/zl=1，對應Q(z0)=4.54 W，當zl增加50%時，對應Q(z0)=5.57 W，換熱量增加22.7%，而當zl減小 50%時，對應 Q(z0)=6.13 W，換熱量增加35%，兩者相差12.3%。因此對于實際的電流引線，當zl不能取最優(yōu)值時，應盡可能增加而不是減小zl。

5 結論

通過對傳導冷卻電流引線的傳熱分析，獲得了電流引線最小漏熱對應的優(yōu)化關系式。通過實例分析了優(yōu)化參數(shù)zl取最佳值時，電流引線兩端溫度及電流與漏熱的關系，結果表明:降低電流引線溫度較高端的溫度，可以有效減小電流引線漏熱;當電流引線的優(yōu)化參數(shù)zl偏離最佳值時，增加zl比減小zl更有利于降低通過電流引線的傳熱量。

1 康志成.大型超導磁體電流引線理論及應用［M］.北京:國防工業(yè)出版社，2009，14-15.

2 范宇峰，龔領會，張 亮，等.制冷機直接冷卻高溫超導磁體電流引線優(yōu)化設計［J］.低溫工程，2005(5):17-21.

3 石 零.低溫真空電流引線熱分析［J］.低溫工程，2005(4):53-55.

4 Ho-Myung Chang，Yeon SukChoi，Steven W Van Sciver.Optimization of operating temperature in cryocooled HTS magnets for compactness and efficiency［J］.Cryogenics，2002，42(12):787-794.

5 康志成，丁立人，翁佩德.超導磁體氣冷電流引線的優(yōu)化設計［J］.核科學與工程，2003，23(4):348-352.