基于Timoshenko梁求解鋼軌導(dǎo)納研究

劉 磊，宣 言，孫加林

(中國鐵道科學(xué)研究院鐵道科學(xué)技術(shù)研究發(fā)展中心，北京 100081)

導(dǎo)納指的是在單位力激勵下結(jié)構(gòu)的響應(yīng)，其倒數(shù)定義為阻抗，表現(xiàn)形式有位移導(dǎo)納、速度導(dǎo)納和加速度導(dǎo)納。鋼軌導(dǎo)納是輪軌表面粗糙度激勵引起輪軌系統(tǒng)響應(yīng)的決定性因素，是進一步研究軌道振動噪聲的基礎(chǔ)。

在鋼軌導(dǎo)納研究中，普遍采用兩種形式的梁模型，即Euler梁和Timoshenko梁模型。Remington將鋼軌看作單層彈性基礎(chǔ)上連續(xù)支撐的Euler梁計算鋼軌導(dǎo)納，所得結(jié)果高頻成分與實測差異較大［1-2］。Thompson在Remington模型基礎(chǔ)上，將鋼軌模型進行擴展，采用多層梁模型取代了單層梁模型，得到了較好的結(jié)果［3-4］。翟婉明通過求解軌道振動微分方程，給出了軌道阻抗的理論解析解［5］。魏偉、翟婉明建立了適合軌道高頻振動導(dǎo)納分析的有限元模型，利用該模型很好地預(yù)測了軌道結(jié)構(gòu)共振［6］。雷曉燕和圣小珍采用多自由度振動體系計算了輪軌接觸點處鋼軌的豎向阻抗［7］。Euler梁考慮鋼軌的彎曲變形而不考慮其剪切變形。Timoshenko梁引入了梁的剪切應(yīng)變，并考慮梁的旋轉(zhuǎn)慣性，從而使梁的受力分析更加完整。

本文利用大型通用有限元軟件Ansys，分別建立Euler梁和Timoshenko梁鋼軌導(dǎo)納分析多層梁模型，采用完全法計算軌道結(jié)構(gòu)在單位力激勵下的頻率響應(yīng)，求解鋼軌導(dǎo)納。

1 鋼軌導(dǎo)納分析模型

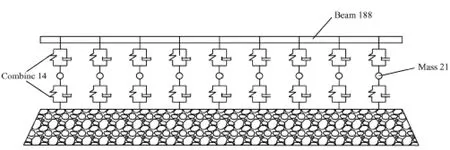
圖1 鋼軌位移導(dǎo)納分析模型

模型采用雙層連續(xù)彈性點支撐模型，建立30 m軌道結(jié)構(gòu)模型，扣件間距0.6 m，如圖1所示。其中鋼軌采用梁單元，扣件系統(tǒng)簡化為彈簧阻尼單元Combine14，軌枕采用集中質(zhì)量單元Mass21，軌枕與道床之間再加入一個Combine14單元來模擬兩者之間的剛度和阻尼。

Combine14單元具有軸向的彈簧—阻尼器選項，是一維的拉伸或壓縮單元。鋼軌分別采用Beam3梁單元和Beam188梁單元模擬。Beam3單元是一種可承受拉、壓、彎作用的單軸單元，可用Beam3單元來表示Euler梁。Beam188單元基于Timoshenko梁理論，是三維線形梁單元，可以考慮剪切變形的影響。

［8］和文獻［9］，模型參數(shù)如下:鋼軌材料楊氏模量E=2.06×1011N/m2，泊松比μ=0.3，材料密度ρ=7 800 kg/m3，阻尼系數(shù)0.02;60 kg/m鋼軌截面面積 A=77.45×10－4m2，鋼軌高度0.176 m，對水平軸慣性矩I=3 217×10－8m4;扣件系統(tǒng)剛度kp=1.2×108N/m，阻尼 cp=7.5×104N·s/m;半根軌枕質(zhì)量m=125 kg。道床系統(tǒng)剛度kb=1.1×108MPa，阻尼cb=5.88×104N·s/m。

2 采用完全法求解鋼軌導(dǎo)納

采用完全法進行頻率響應(yīng)分析，通過用復(fù)數(shù)代數(shù)

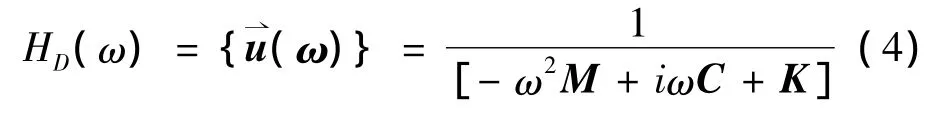
3 計算結(jié)果分析

算法求解一系列耦合的矩陣方程，計算單位力激勵下軌道結(jié)構(gòu)的頻率響應(yīng)。在簡諧激勵荷載作用下，動力學(xué)方程如下

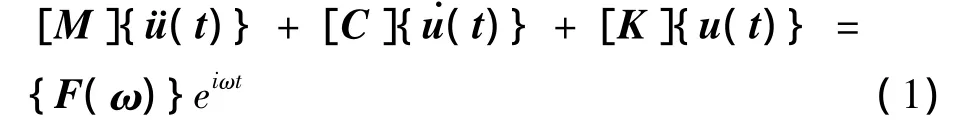
式中，［M］為質(zhì)量矩陣，［C］為阻尼矩陣，［K］為剛度矩陣。

方程的解可寫成如下形式

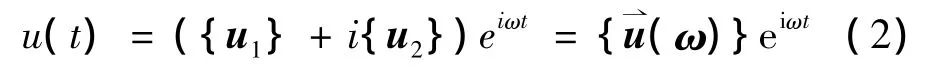
式中，u?(ω)為位移向量，將式(2)代入式(1)可得

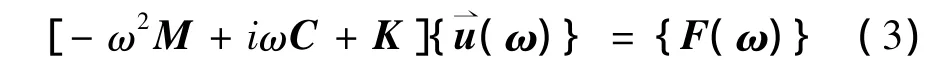
當(dāng)結(jié)構(gòu)受單位荷載作用時，得到軌道結(jié)構(gòu)的位移導(dǎo)納

在Ansys分析中，采用Block Lanczos法提取了鋼軌的前50階模態(tài)，表1列出了鋼軌前10階模態(tài)。

通過觀察鋼軌振動模態(tài)，可以看出鋼軌振型主要有縱向振動、扭轉(zhuǎn)振動、橫向振動和垂向彎曲振動。當(dāng)列車通過時，鋼軌的垂向彎曲振動要比其它振動大得多，是影響鋼軌位移導(dǎo)納的主要因素，提取前10階振動模態(tài)中垂向彎曲振動的固有頻率及振型如圖2所示。

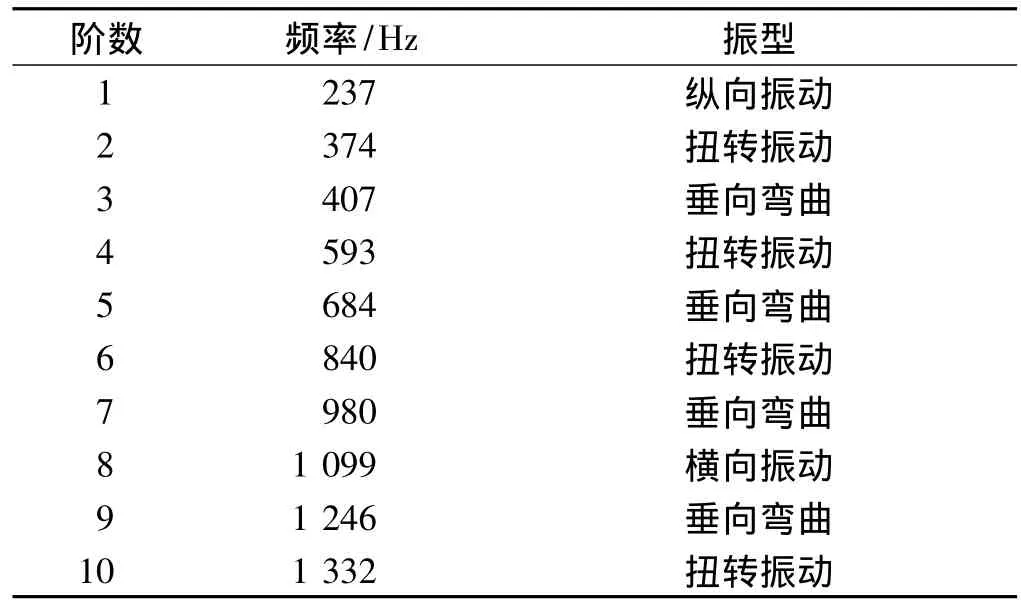
表1 鋼軌前10階模態(tài)固有頻率和振型

圖2 鋼軌垂向彎曲振動固有頻率及振型

分別采用Euler梁和Timoshenko梁建立計算模型，在模型中心位置處施加單位簡諧荷載，采用完全法求解鋼軌位移導(dǎo)納，分析的頻率范圍為0～5 000 Hz，步長為50 Hz，計算得到的鋼軌位移導(dǎo)納頻率響應(yīng)曲線如圖3所示。

由圖3可以看出，在振動頻率1 500 Hz以內(nèi)，采用Timoshenko梁和Euler梁模型的鋼軌位移導(dǎo)納計算結(jié)果基本一致，也與模態(tài)分析結(jié)果相符合，如表2所示。表2為鋼軌模態(tài)固有頻率與兩種梁模型計算的鋼軌位移導(dǎo)納峰值頻率對比。最大峰值發(fā)生在1 250 Hz左右，鋼軌位移導(dǎo)納最大幅值由Timoshenko梁計算為4.19×10－8m/N，Euler梁計算結(jié)果為 3.24 ×10－8m/N，Timoshenko梁計算結(jié)果略大于Euler梁。當(dāng)振動頻率在1 500 Hz以上時，Euler梁計算導(dǎo)納幅值隨頻率的增高而減小，Timoshenko梁模型則仍能較好反映導(dǎo)納的峰—峰值變化規(guī)律。因此，在計算鋼軌位移導(dǎo)納時，分析頻率在1 500 Hz以下時，兩種模型差別不大;當(dāng)計算頻率在1 500 Hz以上時宜采用Timoshenko梁模型。

求解得到鋼軌位移導(dǎo)納HD(ω)，求導(dǎo)即可得到相應(yīng)的速度導(dǎo)納為

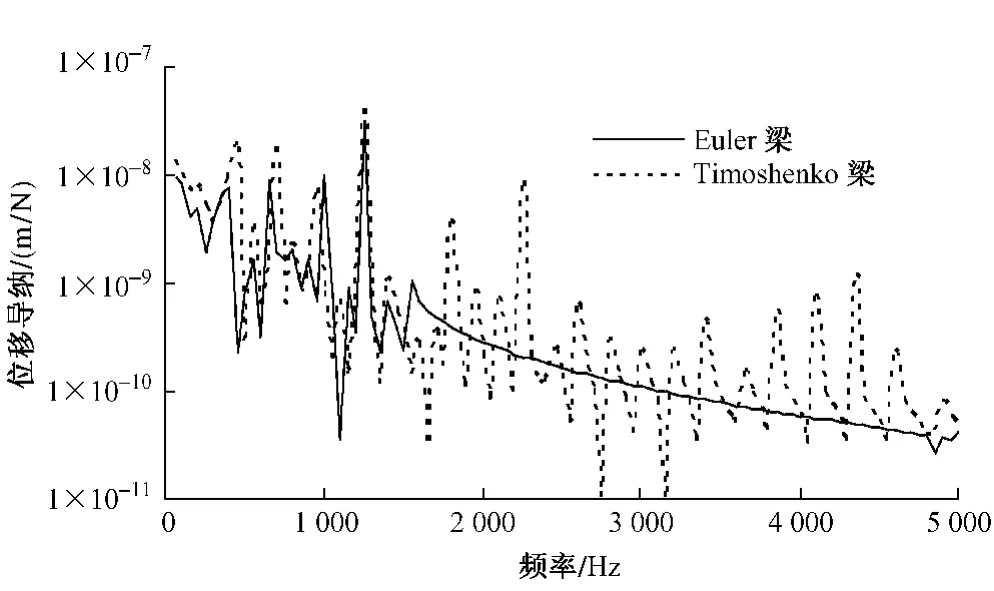
圖3 鋼軌垂向位移導(dǎo)納

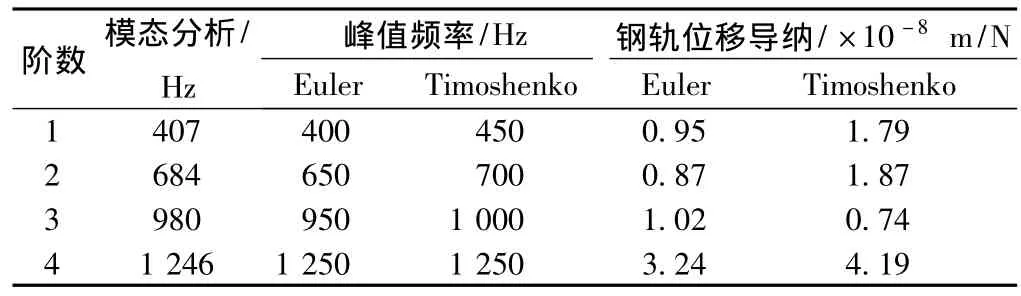
表2 振動模態(tài)頻率與導(dǎo)納峰值頻率對比

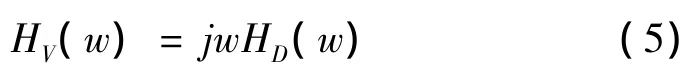
對式(5)繼續(xù)求導(dǎo)即可得到加速度導(dǎo)納

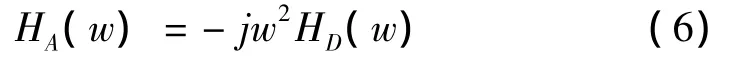
由Timoshenko梁模型計算得到的鋼軌速度導(dǎo)納和加速度導(dǎo)納如圖4所示。速度導(dǎo)納和加速度導(dǎo)納最大峰值頻率均為1 250 Hz，速度導(dǎo)納最大值為5.24×10－5m/s/N，加速度導(dǎo)納最大值為6.55×10－2m/s2/N。頻響曲線的峰值點與固有頻率一一對應(yīng)，且在1 250 Hz時發(fā)生Pinned-pinned振動，即支撐于兩扣件節(jié)點之間的鋼軌受到激勵后產(chǎn)生縱向機械波，其駐波點剛好在兩節(jié)點支撐處。

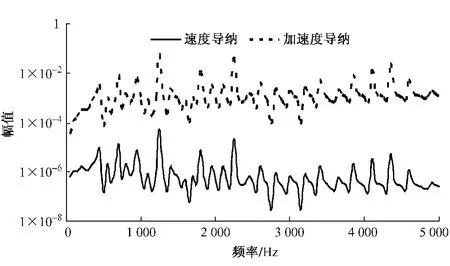
圖4 鋼軌速度導(dǎo)納和加速度導(dǎo)納

4 結(jié)論

1)計算鋼軌導(dǎo)納時，在1 500 Hz以內(nèi)Timoshenko梁和Euler梁模型計算差別不大;當(dāng)頻率高于1 500 Hz時，Timoshenko梁模型能夠較好地反應(yīng)振動的高頻成分。Timoshenko梁模型引入了梁的剪切應(yīng)變，并考慮梁的旋轉(zhuǎn)慣性，從而使梁的受力分析更加完整。

2)鋼軌振型有縱向振動、扭轉(zhuǎn)振動、橫向振動和垂向彎曲振動。采用Timoshenko梁模型計算的前4個垂向位移導(dǎo)納峰值頻率依次為450 Hz、700 Hz、1 000 Hz和1 250 Hz，與模態(tài)分析結(jié)果基本一致。

3)采用Timoshenko梁模型計算的鋼軌導(dǎo)納最大峰值頻率為1 250 Hz，位移導(dǎo)納、速度導(dǎo)納、加速度導(dǎo)納峰值依次為4.19×10－8m/N、5.24 ×10－5m/s/N 和 6.55 ×10－2m/s2/N。頻響曲線的峰值點與固有頻率一一對應(yīng)，且在1 250 Hz時發(fā)生Pinned-pinned振動。

參考文獻

［1］Remington P J．Wheel/rail rolling noiseⅠ:Theoretical analysis［J］．Journal of the Acoustical Society of American，1987，81(6):1805-1823．

［2］Remington P J．Wheel/rail rolling noise Ⅱ:Validation of the theory［J］．Journal of the Acoustical Society of American，1987，81(6):1824-1832．

［3］Remington P J．Wheel/rail noise:Theoretical modeling of the generation of vibrations［D］．University of Southampton，1990．

［4］Thompson D J．Wheel/rail noise generation，PartⅢ:Rail vibration［J］．Journal of Sound and Vibration，1993，161(3):421-446．

［5］翟婉明．鐵路輪軌高頻隨機振動理論解析［J］．機械工程學(xué)報，1997，33(2):20-25．

［6］魏偉，翟婉明．輪軌系統(tǒng)高頻振動響應(yīng)［J］．鐵道學(xué)報，1999，21(2):33-36．

［7］雷曉燕，圣小珍．鐵路交通噪聲與振動［M］．北京:科學(xué)出版社，2004．

［8］郝瀛．鐵道工程［M］．北京:中國鐵道出版社，2000．

［9］翟婉明．車輛—軌道耦合動力學(xué)［M］．北京:科學(xué)出版社，2007．

［10］Thompson D．Railway noise and vibration mechanisms，modelling and means of control［M］．Cambridge:Elsevier，2009．