輕型橋梁轉動體系的研究分析

傅賢超，王正儀，王興猛

(中鐵西南科學研究院，四川 成都 610031)

目前中國新建高鐵及既有鐵路提速快速發展，為了周圍居民的安全，應實行線路全封閉，這必會對鐵路沿線居民正常出行帶來不便，需建設跨線人行天橋來解決由此帶來的影響。為了不影響現有線路的運營，跨線施工中以轉體工藝為最佳方案之一。本文以襄渝鐵路下行線K768+740人行天橋的設計為例，闡述轉體工藝設計的重點。本橋為T形剛構橋轉體設計，橋跨布置為 21.5 m+15 m，長、短跨比為 0.698，根據排水需要及地形情況設置2%單向縱坡。長跨為變截面，采用1.8次拋物線線型，墩頂梁高 1.4 m，端部梁高0.5 m，采用雙肋，肋厚 0.3 m;短跨采用單肋，肋厚1.2 m;橋墩采用1.2 m ×1.4 m 鋼筋混凝土矩形實心墩，墩梁固結[1]。

1 轉盤結構設計

轉盤分為上、下轉盤。下轉盤與基礎相連，下轉盤頂面上設一層2 cm厚Q235鋼板，鋼板底面與下轉盤的預埋鋼筋焊接。鋼板上鋪設一層聚四氟乙烯板，以減小上、下轉盤間的摩擦。為了控制轉動過程中上部梁、墩結構的平衡安全，在下轉盤上設置8個保險腿，并在保險腿之間放置4個豎向千斤頂以微調平衡。上轉盤底面設一層不銹鋼鋼板，其目的是為了進一步減小上、下轉盤間的摩擦系數。上轉盤為2 cm厚Q235鋼板制作成中心下凸的平面轉鉸，如圖1所示。轉體完成后，焊接上、下轉盤中的預埋鋼筋，澆筑之間的空隙，使上下轉盤固結為一個整體[2]。

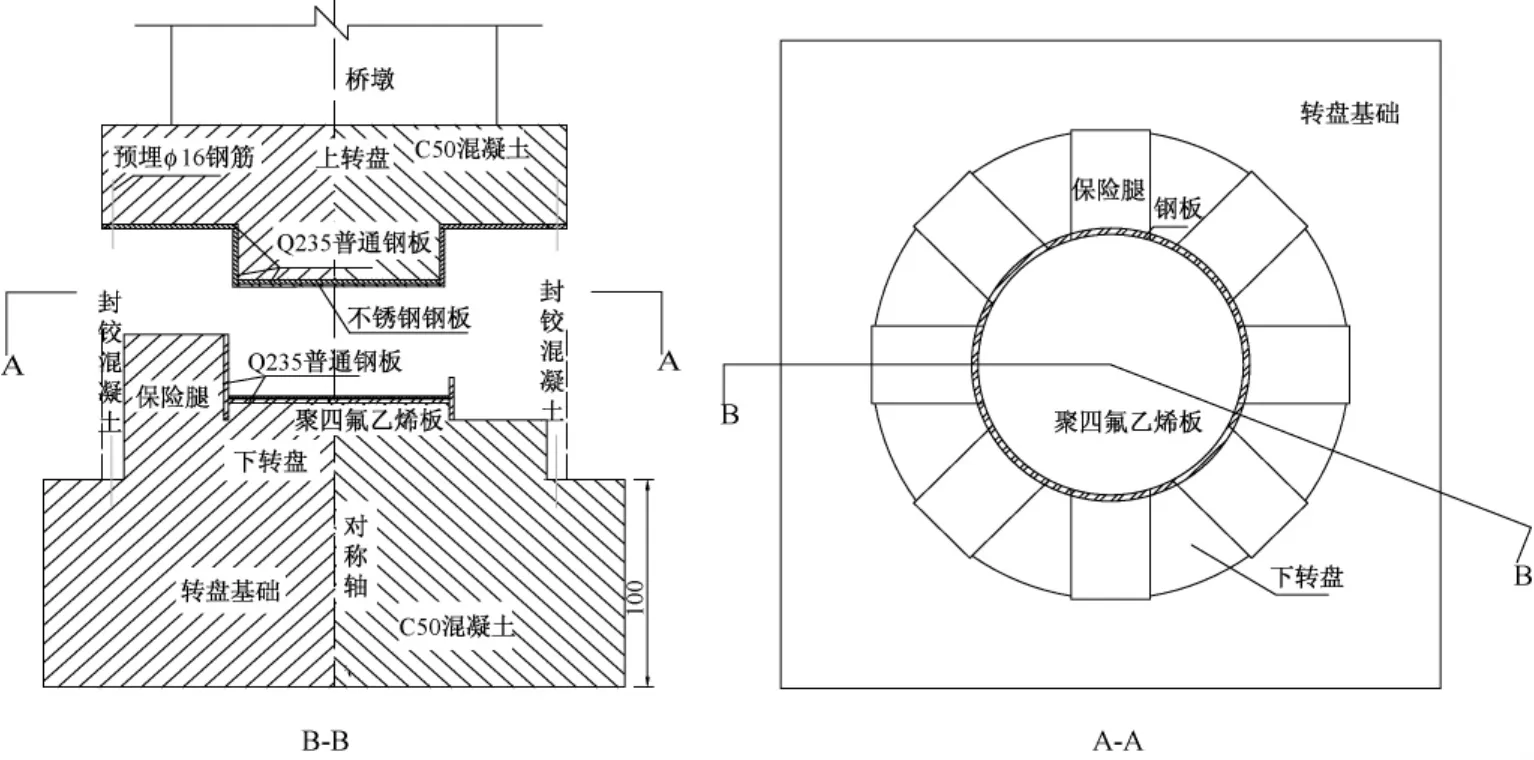
圖1 轉盤立面及平面(單位:cm)

2 轉動牽引力計算

根據以往施工經驗可知轉體靜摩擦系數μg一般為 0.06 ～0.09，動摩擦系數 μd一般為 0.035 ～0.08，施工時可現場實測，并采取如在聚四氟乙烯板上添加黃油等措施來減小靜、動摩擦系數，從而減小牽引力。

轉體牽引裝置設置在上轉盤兩側，轉體系統壓力的形心在2r/3處。根據力矩平衡(圖2)∑M=0可得[3-4]

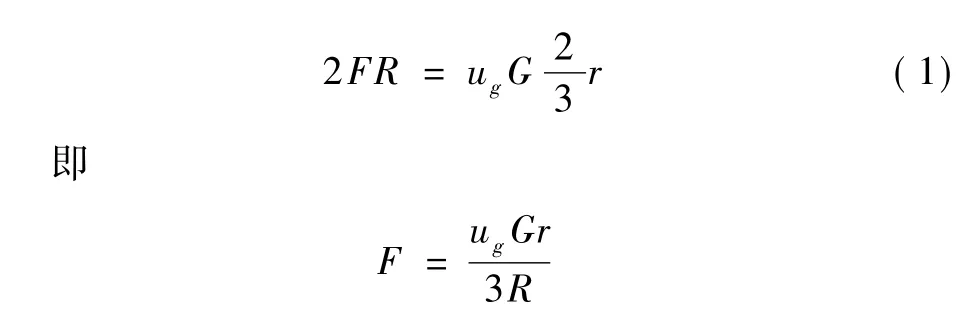
式中，G為轉體重量，R為上轉盤半徑，r為轉鉸半徑。若取 μg=0.08，G=1 500 kN，R=2 m，r=1 m，則 F=20 kN。

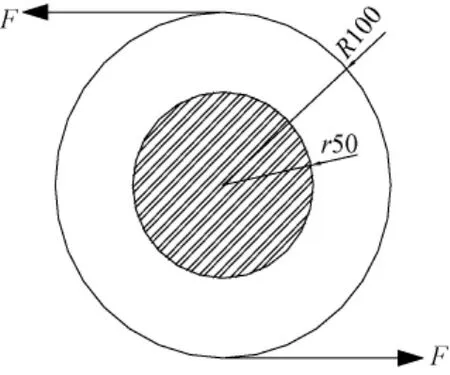
圖2 牽引計算圖式

牽引動力可由兩臺5 t的卷揚機提供。由于卷揚機的性能不易根據實際情況控制速度，兩邊拉力不易平衡，降低了轉體穩定性。在實際施工過程中用手拉鏈條葫蘆代替卷揚機，通過人工曳動手鏈條使手鏈輪轉動，將摩擦片棘輪、制動器座壓成一體共同旋轉，從而達到牽引的目的。如何保證兩端牽引力大小一致，可按如圖3和圖4所示布置，根據轉動方向確定鋼絲牽引繩纏繞方向，如轉動方向為順時針，則A端牽引繩順時針向上纏繞3圈，B端順時針向下纏繞3圈，纏繞圈數由上轉盤邊緣轉動距離確定(一般兩端牽引繩各纏繞3圈)。A端纏繞3圈之后通過兩個定滑輪改變牽引方向，與B端牽引繩平行，B端牽引繩穿過 C滑輪，與A端牽引繩用U型螺栓擰緊，從而可保證A，B兩端牽引力大小一致，而C滑輪另一端連接手拉鏈條葫蘆。手拉鏈條固定端安裝一個拉力讀數器，牽引力大小可隨時從儀器上讀取。表1所示為襄渝鐵路跨線部分人行天橋實測牽引力以及計算得到的靜摩擦系數、動摩擦系數。

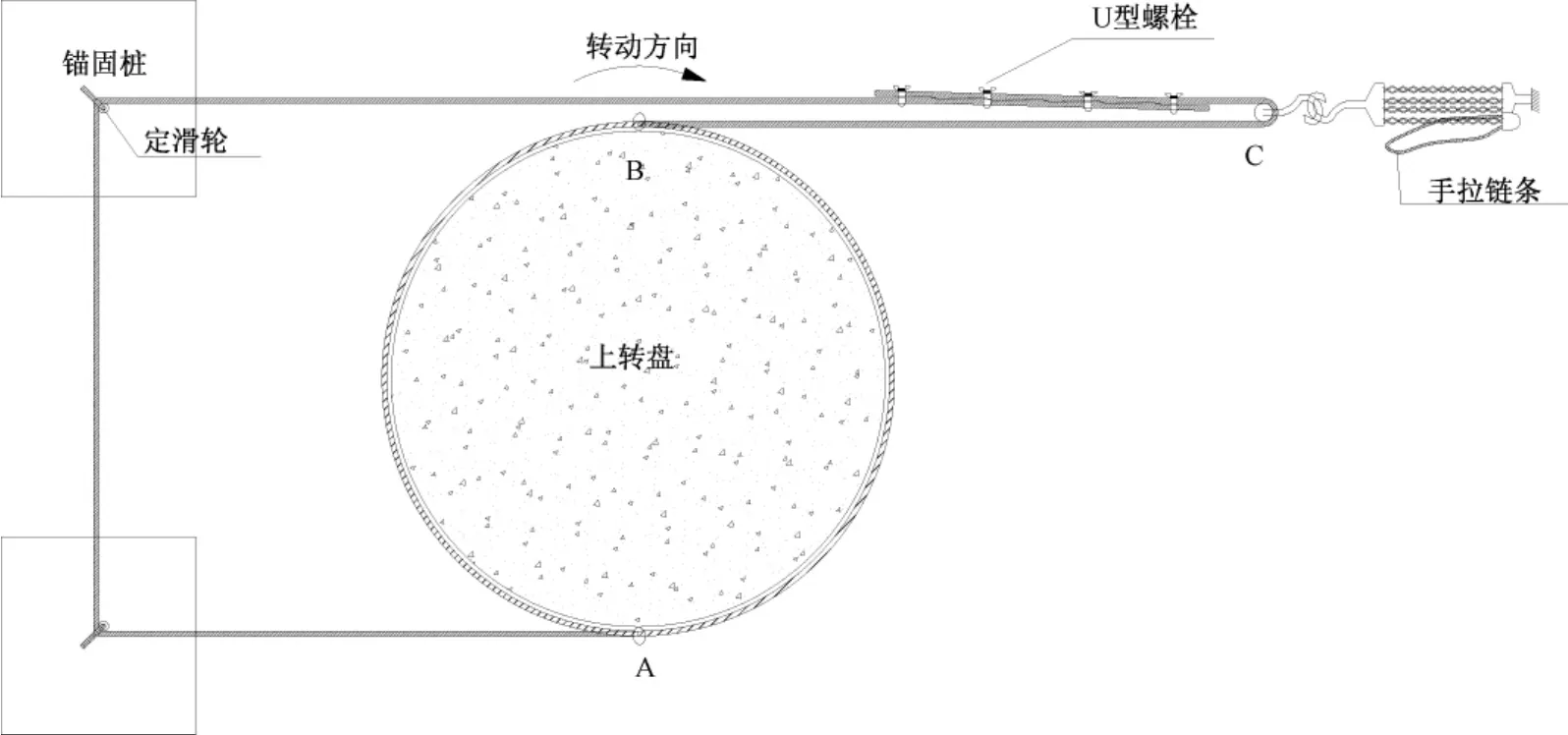
圖3 牽引裝置平面

圖4 牽引裝置立面圖

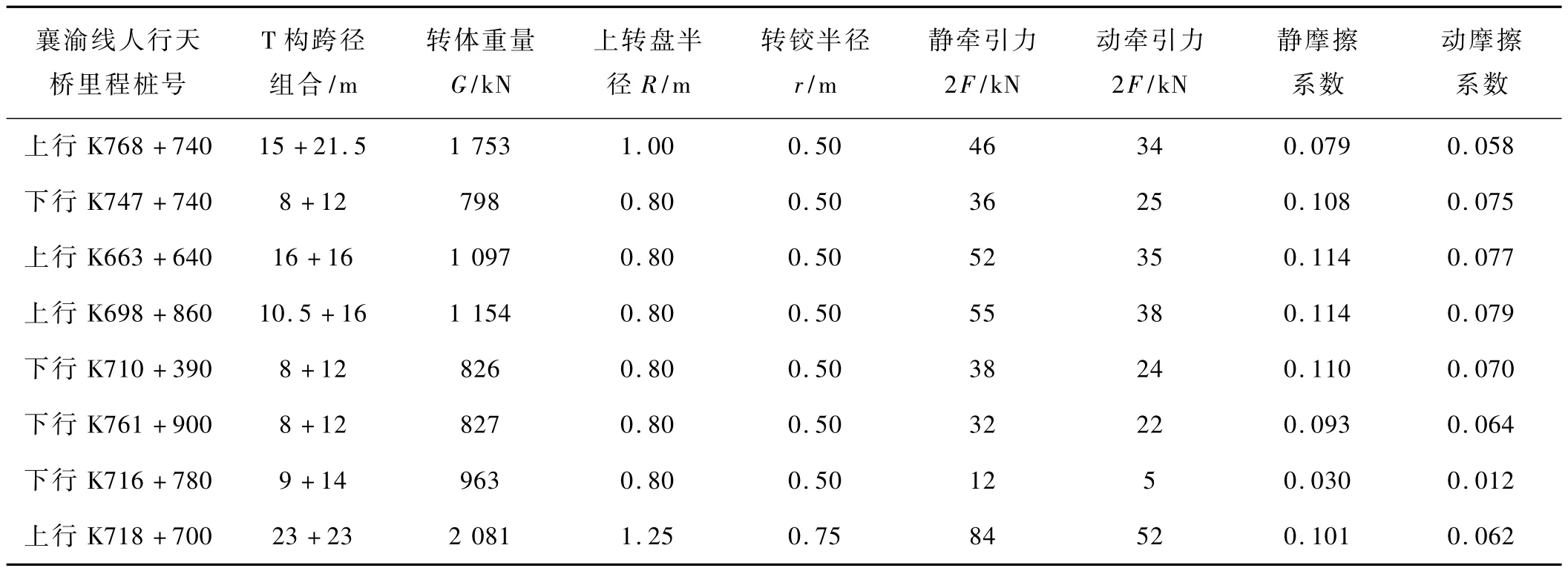
表1 襄渝鐵路跨線人行天橋牽引力數據

3 轉盤應力驗算

轉盤結構采用C50鋼筋混凝土，上部結構為T形不對稱懸臂剛構，密度按2.6 t/m3計算，根據模型計算可知主梁和橋墩總重為1 280 kN，平衡重(配重)為135 kN，考慮安全系數和施工臨時荷載，轉體上部結構按施加1 500 kN重量計算。采用有限元分析軟件建模，結果如圖5所示(負值為壓應力，正值為拉應力，單位為Pa)。轉盤最大壓應力為4.04 MPa，最大拉應力為0.89 MPa，應力滿足設計要求。設計中上、下轉盤均用鋼板套箍，不但減小轉體的靜、動摩擦系數，同時也增加了轉盤的強度，使結構更加安全可靠[5]。

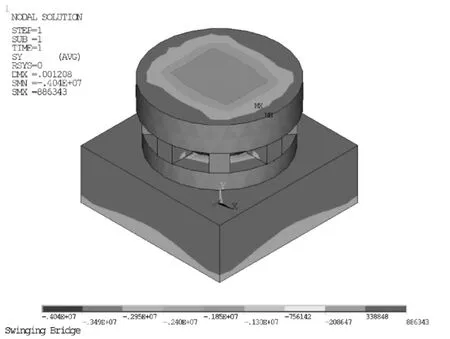
圖5 轉體結構豎向應力云圖(單位:Pa)

4 抗傾覆穩定性計算

由于本橋設計為不對稱布置，通過在短跨邊施加平衡重以達到轉體平衡。由于施工誤差和結構參數誤差的存在，實際情況很難達到理論上的完全平衡，這就需要計算橋梁在配重作用下的穩定性，以免發生傾覆。

結構靜力計算的方程可表示為

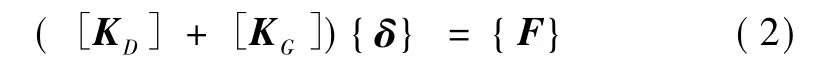
其中，[KD]為結構彈性剛度矩陣，對桿系結構反應了其單元截面剛度EA和EI的影響;[KG]為幾何剛度矩陣，也稱為初始應力矩陣，與桿系結構與桿件的長度、位置和初始軸力有關。幾何剛度矩陣使單元剛度發生了變化，主要是由于軸力在桿彎曲時產生的效應所致。

根據式(2)可以求得在{F}作用下的位移{δ}，如荷載不斷增加，則結構位移不斷增大。由于[KG]與荷載大小有關，這時結構的力與位移不再是線性關系，如{F}達到 λσ{F}時，結構達到隨遇平衡狀態，這就是所要求的臨界荷載。若{F}增加至λ倍，則內力和幾何剛度也增加至λ倍，由(2)式可得

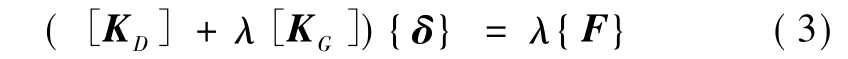
如λ足夠大，使得結構達到隨遇平衡狀態，即當{δ}增加{Δδ}時，上列平衡方程也能滿足，即有

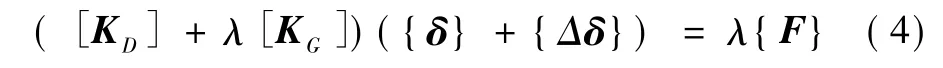
同時滿足式(3)和(4)的條件是

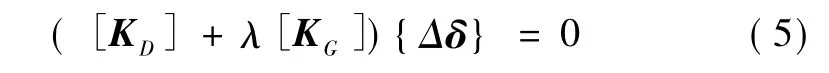
式(5)就是計算結構穩定安全系數的結構方程式，若方程有 n階，則理論上存在 n個特征值 λ1，λ2，…，λn，但工程上只有最小的特征值或最小的安全系數才有實際意義，這時的特征值為 λσ，臨界荷載為 λσ{F}。

根據有限元模型的計算分析可得，轉動過程中橋梁結構在配重作用下的穩定系數為3.39(如圖6所示)，而規范規定，施工中的橋梁結構穩定系數不得小于2，故本橋抗傾覆穩定性滿足要求。

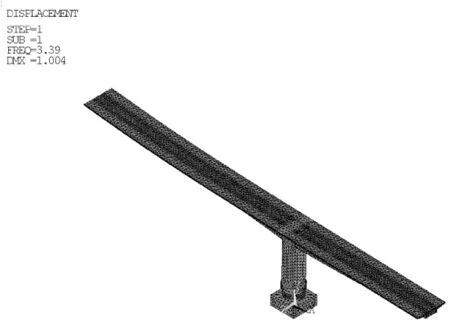
圖6 懸臂狀態在配重作用下結構的穩定系數

5 抗風穩定性計算

轉體結構在不同的地區和不同的季節有不同的抗風標準。根據《鐵路橋涵設計規范》，風荷載應該按下式進行計算。

式中 W——風荷載(Pa);

W0——基本風壓值;

K1——風載體形系數;

K2——風載高度變化系數;

K3——地形地理條件系數。

根據全國基本風壓圖可查詢得到重慶地區(橋梁所在地)基本風壓值W0=0.3 kN/m2，但考慮到鐵路地形的特殊性，應按風力等級來考慮。正式轉體時(懸臂狀態)要求風力不超過6級，因此以最大風力來計算結構的抗風穩定性。風力為6級時的最大風壓值W=v2/1 600=312/1 600=0.6 kN/m2。根據《鐵路橋涵設計規范》，綜合橋梁設計，取主梁K1=1.2，橋墩K1=1.4;K2=1.0;K3=1.2。則主梁上的風荷載為 WZ=0.864 kN/m2，橋墩上的風荷載為 WD=1.008 kN/m2。計算結果表明，橋梁在風荷載作用下的穩定系數達到了26.58，如圖7所示，遠遠大于規范要求，故抗風穩定性滿足要求。

圖7 懸臂狀態在風荷載作用下結構的穩定系數

6 結語

設計中應對每一個施工階段進行計算分析。當脫架完成，梁體處于懸臂狀態階段，結構最不穩定，故文中轉體結構應力驗算、平衡重下的穩定分析和抗風穩定性均以懸臂狀態為準。計算結果表明轉體結構轉動過程中內力和穩定性均滿足設計要求。目前該橋及后續數十座橋已成功轉體，轉鉸均為通用設計，節省了設計費、轉鉸加工及安裝費，降低了工程造價。本項技術為以后輕型橋梁轉體設計提供了參考。

[1]王興猛，傅賢超，曹文.襄渝鐵路線下行 K768+740人行天橋設計說明書[R].成都:中鐵西南科學研究院，2010.

[2]曹文，王正儀，王興猛.輕型橋梁轉體施工專項試驗研究[J].鐵道建筑，2011(12):13-15.

[3]張聯燕，譚邦明，陳俊卿，等.橋梁轉體施工[M].北京:人民交通出版社，2001.

[4]中華人民共和國交通部.JTJ 041—2000 公路橋涵施工技術規范[S].北京:人民交通出版社，2000.

[5]張立明.Algor、Ansys在橋梁工程中的應用方法與實例[M].北京:人民交通出版社，2005.