長定子中低速磁浮列車軌道非線性有限元分析
何 嵐,劉 放,邢 濤,周 益
(西南交通大學 機械工程研究所,四川 成都 610031)
磁浮列車按直線電機定子長度分為長定子直線電機和短定子直線電機。長定子直線電機的定子(初級線圈)設置在導軌上,其定子繞組可以在導軌上無限長地鋪設,故稱為“長定子”,常用在高速及超高速磁浮鐵路中。短定子直線電機的定子設置在車輛上。由于其長度受列車長度的限制,故稱為“短定子”。短定子直線電機通常用在中低速磁浮鐵路及直線電機輪軌道交通中,用于城市軌道交通領域[1]。在研究長定子應用于中低速磁浮列車軌道時,為限制振動給中低速磁浮列車帶來的危害和影響,在磁浮列車軌道中應用彈性體,以充分發揮其隔振和調整高度的作用。但實際工程中,彈性體和軌道支座之間以及軌枕與彈性體之間是接觸的,屬非線性行為。為了更恰當地對軌道承載情況進行分析,在此,采用非線性接觸分析進行計算。通過計算,一方面可對磁浮列車軌道情況進行較系統的分析,同時也為了更好地研究承壓彈性體結構對軌道性能的影響,對其主要的設計參數進行系統的研究,提出軌道承壓彈性體主要結構尺寸的合理選取范圍。這對以后磁浮列車軌道承壓彈性體的設計和應用有較重要的理論意義和實用價值。
1 磁浮列車軌道非線性有限元分析
1.1 磁浮列車軌道結構
傳統軌道由鋼軌、軌枕、路基等組成。磁浮列車軌道因為安裝電磁鐵以及列車懸浮和導向的需要,其結構與傳統軌道有較大區別,特別是鋼軌和軌枕部分。磁浮列車軌道的結構為軌道立柱上面安裝枕梁安裝座,枕梁安裝座與枕梁之間安裝承壓彈性體,枕梁上面安裝鋼軌。鋼軌與軌枕采用螺栓連接。鋼軌的活動軌與固定軌之間采用軌道連接板焊接[2-3]。圖1是軌道橫截面示意圖。

圖1 軌道橫截面示意
1.2 軌道建模及有限元分析
這里的有限元模型只針對軌道的固定立柱、枕梁安裝座、承壓彈性體、軌枕和鋼軌。有限元建模的原則是既準確進行結構的力學特性仿真計算,又盡可能使模型簡單。在建立軌道模型時,嚴格遵守原則對實際結構進行簡化,模型的主要尺寸和實際結構相同,但簡化了部分工藝結構和電氣安裝結構。
直軌軌道沿中心線對稱,建模時可以沿軌道縱向對稱中心面將軌道進行剖分,取軌道結構的二分之一作為計算模型。對曲線軌道則不可做這樣處理,所以建模時沒進行剖分,如圖2。

圖2 中低速磁浮列車軌道Solidworks模型
磁浮列車長8.7 m,約20 t,共6塊電磁鐵,沿縱向中心面對稱布置,每邊3塊,電磁鐵之間間隔72 mm。根據電磁鐵的結構和布置方式,磁浮列車作用于軌道的荷載可以簡化為沿軌道方向鋼軌表面三個區域的均布荷載(見圖3),每個區域一段,每段2.9 m,段與段間隔72 mm。將列車重量處理成均布荷載后,荷載大小q=0.018 MPa,平均作用于三節連續的鋼軌下表面,軌道立柱下表面為全約束。
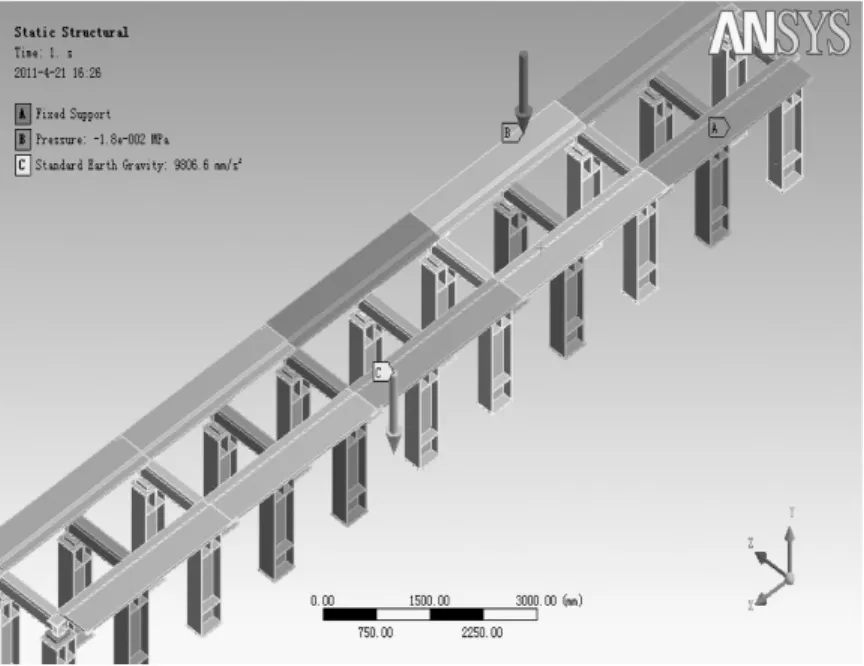
圖3 磁浮列車軌道荷載和約束施加
1.3 軌道非線性有限元計算結果
鋼軌、軌枕和固定立柱材料為 Q235鋼,彈性模量 為 2.06×105MPa,泊 松 比 為 0.3,密 度 為7 800 kg/m3。承壓橡膠板加在枕梁安裝座與軌枕之間,為接觸非線性行為[4],摩擦系數分別取 0.7和0.2。承壓彈性體材料為聚氨酯橡膠[5],彈性模量為4 000 MPa,泊松比 為0.499 8,密度為1 300 kg/m3。枕梁安裝座實際材料為混凝土,其彈性模量為30 000 MPa,泊松比為 0.2。
圖4,圖5和圖6分別是由 ANSYS Workbench有限元分析得到的軌道總靜位移等值線圖和應力等值線局部放大圖及單節鋼軌變形曲線圖。

圖4 軌道總靜位移等值線
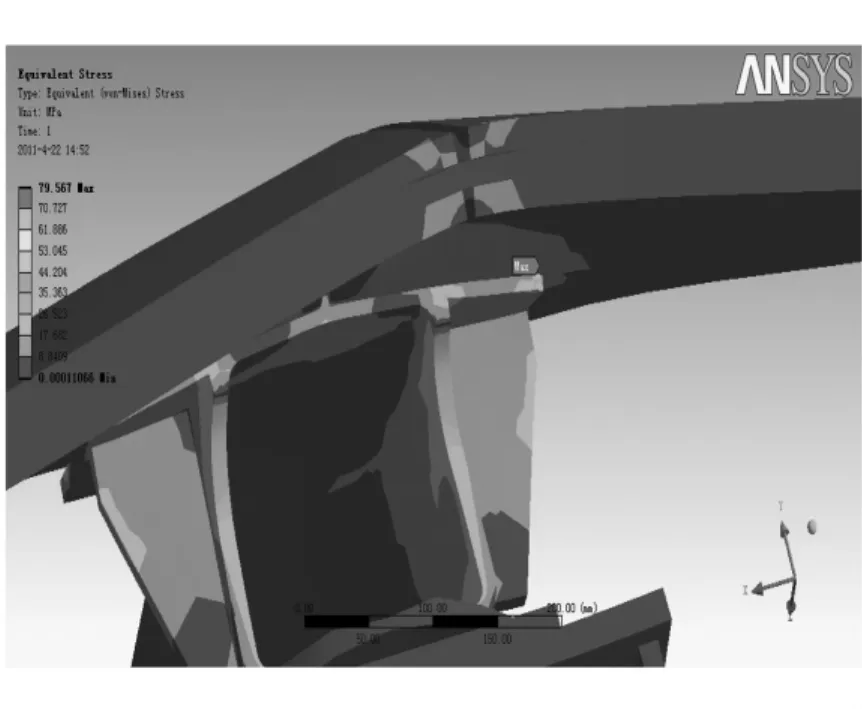
圖5 軌道應力等值線局部放大

圖6 單節鋼軌變形曲線
從計算結果可見:中低速磁浮列車的鋼軌和軌枕的最大應力都不大。磁浮列車軌道最大應力發生在軌枕外端支撐鋼軌的位置,最大約為79.567 MPa,為局部應力集中,其它部分應力較小,約8.841~17.882 MPa,特別是鋼軌的應力較小,大部分區域的應力均<8.841 MPa。
從圖5可以看出,中低速磁浮列車軌道在垂直荷載的作用下,最大變形發生在鋼軌的最外側,為0.616 37 mm,鋼軌變形對磁浮列車運行有較大影響。當軌道剛度不夠時,會產生較大變形,導致位于鋼軌中間部位的傳感器檢測到的相對位置信號失真,從而影響控制單元對電流、電磁力大小的控制,引起列車的振動。所以,鋼軌的變形越小越好,可通過對承壓彈性體的分析研究得出減小鋼軌變形的合理方法。
2 兩種支撐下軌道幾項重要數據對比分析
為充分發揮承壓彈性體隔振、吸收部分荷載、調節高度的作用,利用非線性接觸有限元分析方法分別計算了承壓彈性體與枕梁安裝座間取不同摩擦系數情況下軌道的最大等效應力、變形及軌道垂直振動頻率和橫向振動頻率,具體情況如表1所示。
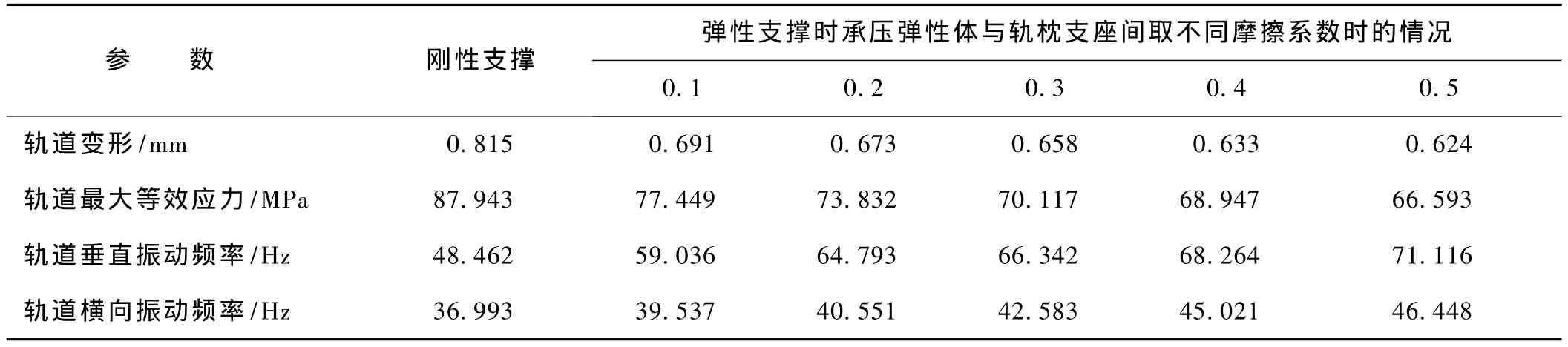
表1 不同支撐情況下的軌道參數
分析表1可知,中低速磁浮列車軌道軌枕與軌枕支座間安裝承壓彈性體后,軌道變形減小,軌道的垂直振動頻率和橫向振動頻率都大幅提高,有利地避免了軌道共振,承壓橡膠板起到良好隔振、吸收部分荷載、調節高度的作用。另外,彈性支撐時,軌道最大等效應力也比剛性支撐時小很多。這主要是由于承壓彈性體的彈性壓縮發生鍋底狀變形[5-6],導致軌道受壓產生的預應力抵消了部分軌道拉應力所引起的變形,這對軌道的受力有利。
另外,由表1還可以看出,在垂直荷載作用下,當承壓彈性體和枕梁安裝座間取不同的摩擦系數時,軌道剛度、強度及主要振動頻率也是變化的。隨著摩擦系數的增大,軌道最大變形和最大應力減小,頻率則隨之增大。由此可知,在實際工程應用中,為了增大軌道的安全度,在允許的范圍內應該盡可能地增大承壓彈性體和枕梁安裝座間的摩擦。
3 承壓彈性體厚度及面積對軌道性能的影響
軌道承壓彈性體的主要功能是將軌道上部結構反力可靠地傳遞給枕梁支座,還能適應軌枕端轉動及通過彈性支座的剪切變形來適應軌枕由溫差引起的伸縮變形。其優點主要表現在:結構簡單,建筑高度低,安裝、更換方便,有較長的使用期限;能適應軌道上部結構在各方面的變形。另外,當磁浮列車通過軌道時,彈性支座能均勻分布水平力,吸收部分振動,調整高度,從而延長軌道壽命。
為充分研究承壓彈性體厚度及面積對軌道性能的影響,利用參數化有限元分析技術分別計算了厚度不同情況下軌道的最大等效應力、變形及頻率,具體情況如表2所示(D為承壓彈性體直徑、H為承壓彈性體厚度)。面積不同情況下軌道的最大等效應力、變形及頻率的具體情況如表3所示。
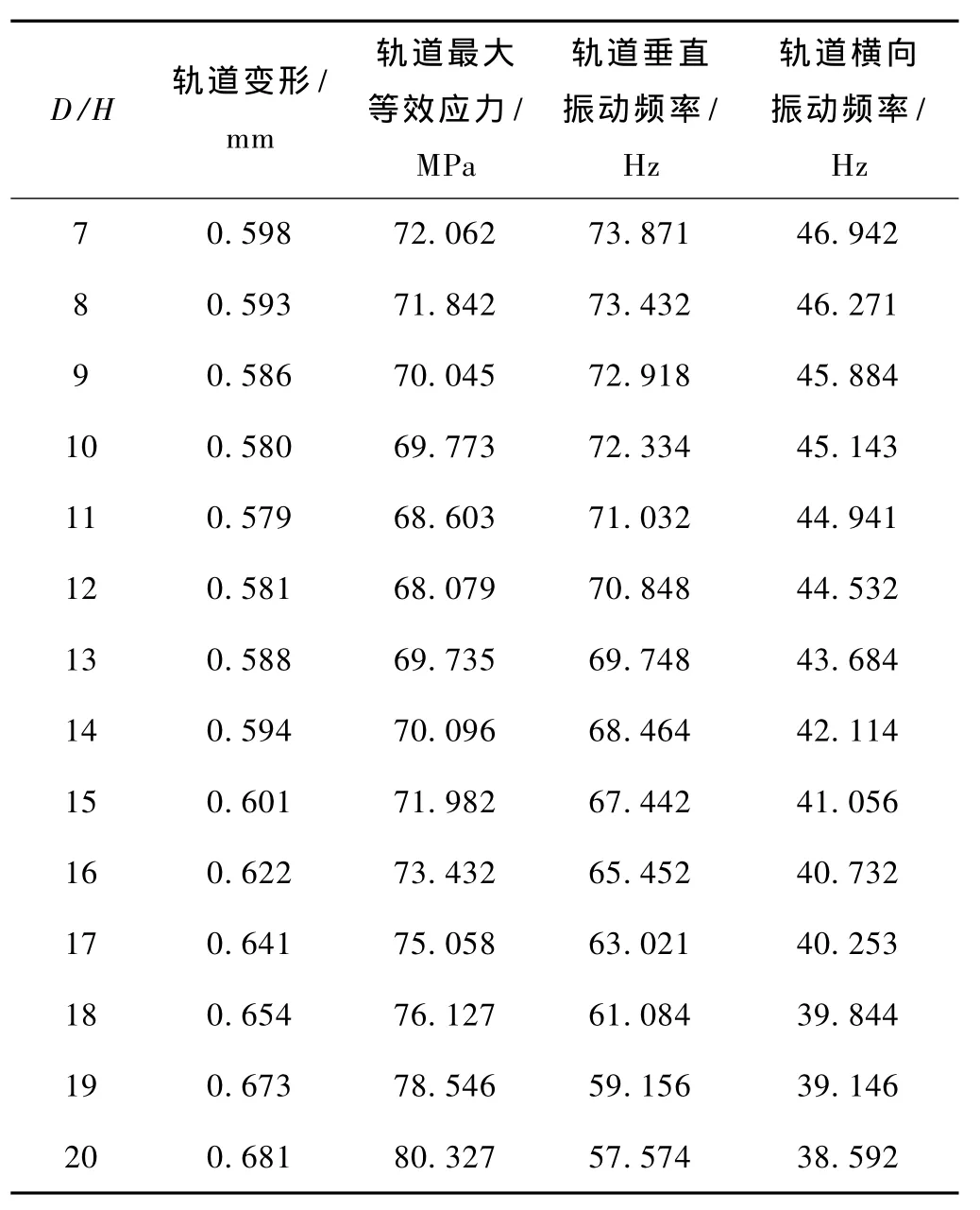
表2 不同厚度承壓彈性體對應的軌道性能參數
根據表2可以得到:在相同荷載情況下不同承壓彈性體厚度對應軌道總位移的變化曲線,如圖7(a)所示。同樣,根據表2可以得到:在相同荷載情況下軌道的最大應力變化曲線如圖7(b)所示;軌道垂直振動頻率變化曲線如圖7(c)所示;軌道橫向振動頻率變化曲線如圖7(d)所示。
從表2可知,中低速磁浮列車軌道承壓彈性體厚度減小,軌道最大變形和最大應力都成非線性變化。從圖7(a)和圖7(b)可以看出,荷載相同時的不同厚度承壓橡膠板對應的軌道位移及應力曲線變化類似一條二次曲線。在 D/H介于9~15之間,變化比較平穩。承壓橡膠板的直徑與厚度比值取此區間比較合適。從圖7(c)和圖7(d)可以看出,增加磁浮列車軌道承壓彈性體的厚度,有利于提高軌道垂直振動頻率和橫向振動頻率,避免共振發生,也有利于調節磁浮列車軌道高度。

表3 不同面積承壓彈性體對應的軌道性能參數
根據表3可以得到:在相同荷載情況下不同承壓彈性體面積對應軌道總位移的變化曲線,如圖8(a)所示。同樣,根據表3還可以得到:在相同荷載情況下,軌道的最大應力變化曲線如圖8(b)所示;軌道垂直振動頻率變化曲線如圖8(c)所示;軌道橫向振動頻率變化曲線如圖8(d)所示。
從圖8可以看出,荷載相同時,不同面積承壓彈性體對應的軌道位移及應力曲線變化類似一條二次曲線。在D/H介于14~19之間,變化比較平穩。承壓彈性體的直徑與厚度比值取此區間,比較合適。
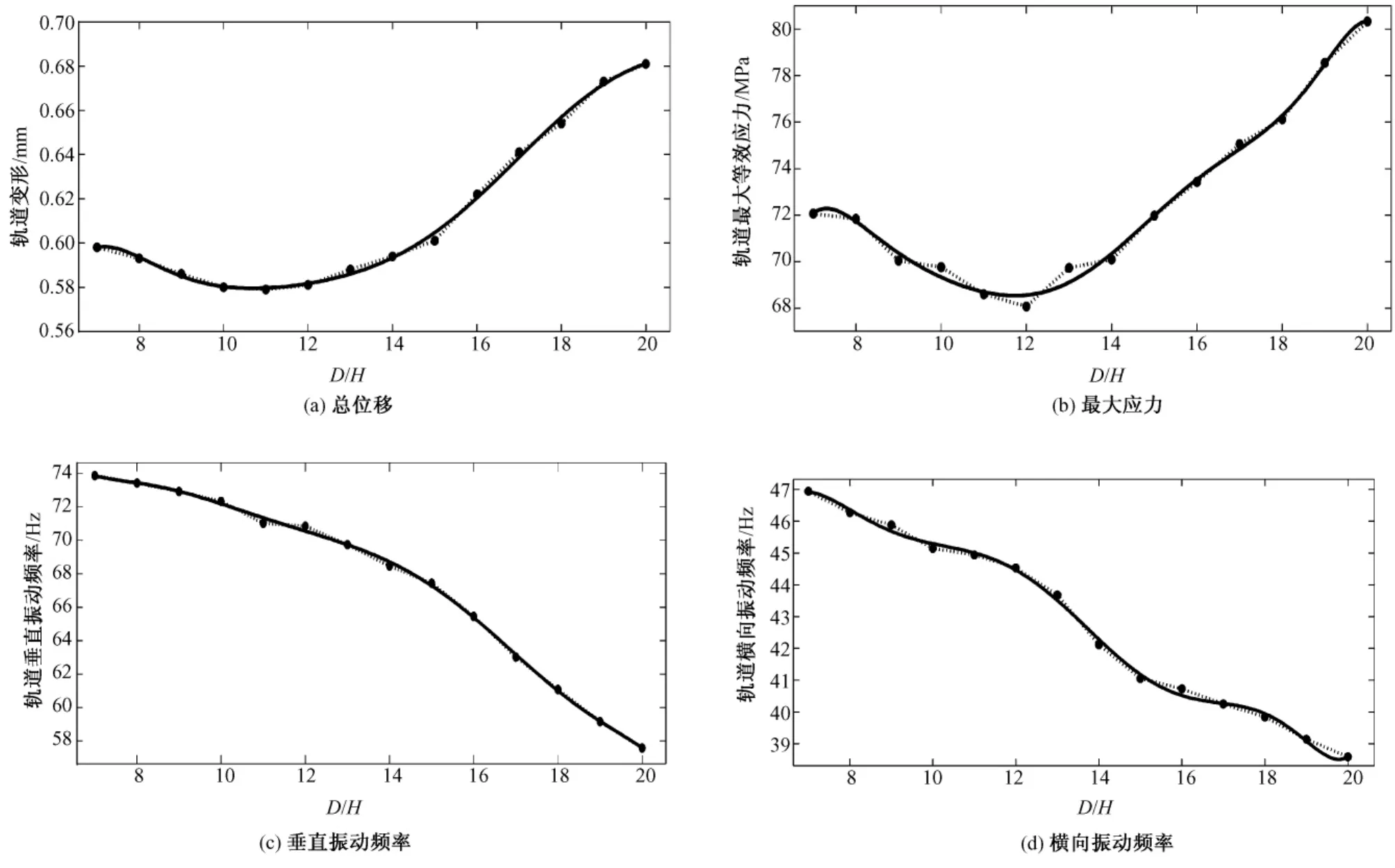
圖7 不同厚度D/H承壓彈性體對應的軌道總位移、最大應力、垂直和橫向振動頻率曲線
從分析結果可知,中低速磁浮列車軌道應用承壓彈性體后,軌道垂直方向上的變形都比較小,有利于控制單元檢測到可靠的相對位置信號,減小了列車的振動,承壓彈性體充分發揮了隔振、吸收部分荷載和調節高度的作用,使列車運行更加平穩舒適。
4 結論
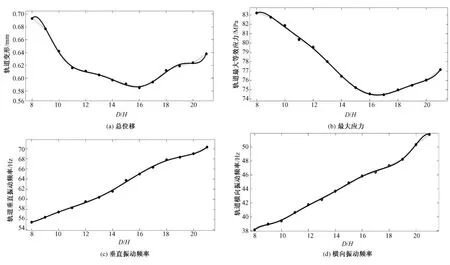
圖8 不同面積D/H承壓彈性體對應的軌道總位移、最大應力、垂直和橫向振動頻率曲線
1)將材料非線性和接觸有限元模型應用到中低速磁浮列車軌道的分析計算中,獲得了比較滿意的計算結果,為以后計算此類問題提供了一種有效方法。
2)當軌枕放在彈性支承(如承壓彈性體)上時,磁浮列車軌道上所受的拉應力較軌枕放在剛性支承上時要小。這主要是由于承壓彈性體的彈性壓縮,使承壓彈性體發生鍋底變形,抵消了部分軌道拉應力引起的變形。承壓彈性體起到了良好的隔振、吸收部分荷載和調整軌道高度的作用。
3)在垂直荷載作用下,承壓彈性體和枕梁安裝座之間的摩擦系數越大,軌道最大變形和最大應力越小,頻率則越大。因此,在實際工程應用中,為了增大軌道的安全度,在允許的范圍內,應該盡可能地增大承壓彈性體和枕梁安裝座間的摩擦。
4)通過研究,得到了中低速磁浮列車軌道同一面積下承壓彈性體厚度比較恰當的取值范圍(彈性體直徑與厚度比應取9~15之間)和同一厚度下承壓彈性體面積比較恰當的取值范圍(彈性體直徑與厚度比應取14~19之間)。
[1]沈志云.高速磁浮列車對軌道的動力作用及其與輪軌高速鐵路的比較[J].交通運輸工程學報,2001(1):1-6.
[2]吳曉,程文明,劉放.基于ANSYS的磁浮軌道結構分析與優化設計[J].機械設計與制造,2006(5):5-7.
[3]趙春發,翟婉明.磁懸浮車輛隨機振動響應分析及其平穩性研究[J].中國機械工程,2002,13(16):1402-1406.
[4]劉岳兵,王少華,李梅,等.盆式橡膠支座結構及混凝土墩臺非線性有限元分析[J].鐵道建筑,2010(9):28-30.
[5]莊軍生,張士臣.大噸位盆式橡膠支座的試驗研究[J].鐵道建筑,1989(10):1-6.
[6]顧云,滕念管.溫差作用下磁浮軌道梁變形分析及比較[J].鐵道建筑,2011(6):18-20.

