基于ABAQUS非線性接觸分析的球型支座轉動性能及結構分析

李冰，王少華，嚴情木

(1.西南交通大學新型驅動技術中心，四川成都 610031;2.西南交通大學機械工程研究所，四川成都 610031)

橋梁支座是連接橋梁上部結構和下部結構的重要結構部件。它能將橋梁上部結構的反力和變形(位移和轉角)可靠地傳遞給橋梁下部結構，以適應梁體自由伸縮及轉動的需要。目前應用廣泛的橋梁支座形式有板式橡膠支座、盆式橡膠支座、球型支座等［1］。板式橡膠支座結構簡單、成本低廉，但承載能力較低;盆式橡膠支座承載能力較高、滑動摩擦系數小、轉動靈活，但橡膠材料易老化、設計轉角較小［2-3］;球型支座設計轉角可遠大于盆式橡膠支座，一般為0.01～0.02 rad，必要時也可以達到0.05 rad，承載能力高，可適應于大跨度橋梁的應用。球型支座在轉動力矩作用下，會在轉動接觸面之間發生較大位移和轉動，對結構承載方式會產生顯著影響，必須在分析中加以考慮。通過建立常規力學模型分析球型支座轉動性能，并通過非線性接觸有限元分析方法進行驗證，確定球型支座的轉動條件。研究不同轉角下球型支座各部件應力分布情況，在此基礎上，研究了球型支座主要設計參數對支座性能的影響。分析計算結果對以后球型支座的優化設計和應用有重要的理論意義和實用價值。

1 球型支座的轉動分析

1.1 球型支座結構

球型支座基本結構示意如圖1［4］。

圖1 球型支座基本結構示意

1.2 球型支座力學模型分析

在轉動力矩作用下，球型支座在球面四氟板處發生轉動［1］，建立球型支座力學模型如圖2所示。圖中，m為上部結構質量，P為球型支座所受的正壓力，R為球面曲率半徑，e為上部結構由于轉動產生的重力偏心距。

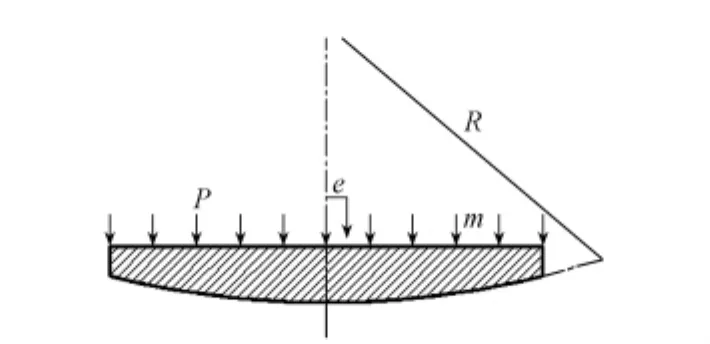
圖2 球型支座轉動示力圖

建立該系統的平衡方程為

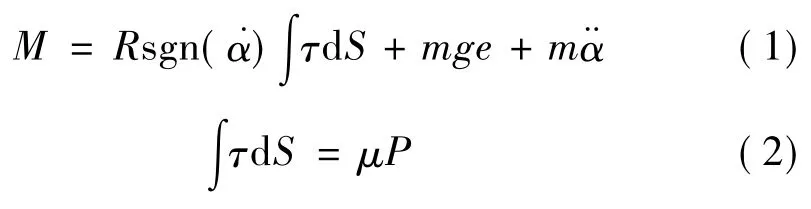
式中，M為施加的轉動力矩，τ為球面單位面積摩擦力，μ為摩擦系數，為角速度，為角加速度，sgn為符號函數，其值為

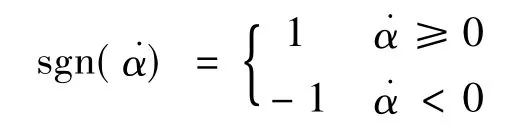
由于實際轉動過程中產生的重力偏心距e相對于球面曲率半徑R很小，球型支座可以視為勻速轉動，因此式(1)可以簡化為

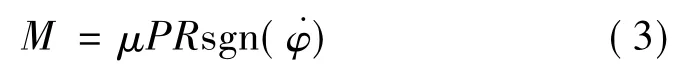
由上式可以看出，轉動力矩M與正壓力P、摩擦系數μ、球面半徑R近似成正比例關系，球型支座一旦克服摩擦就可以發生轉動，此時轉角的大小與轉動力矩幾乎無關，因此球型支座可以適應各種轉角的需要，同時為了防止出現過大的轉角而使結構安全得不到保證，需要安裝限位裝置。

1.3 球型支座有限元模型

由于球型支座結構的對稱性，建立球型支座的1/2實體模型進行有限元建模和計算。接觸類型選擇有限滑動，這種接觸類型允許接觸面之間出現任何大小的相對滑動和轉動，適用于大位移非線性接觸分析。在為接觸分析選擇單元類型時，將會構成從面的模型部分選用一階單元，使計算結果更容易收斂［5］。球型支座中鑄鋼結構彈性模量E=2.05×105MPa，泊松比v=0.3，聚四氟乙烯材料彈性模量E=1 500 MPa，泊松比v=0.4，混凝土結構彈性模量E=3.3×104MPa，泊松比v=0.2。

支座豎向承壓，載荷大小為10 MN，為了使模型和計算結果與實際工況更加符合，需要加入橋跨結構和墩臺結構，并研究橋跨結構底面積大小對球型支座受力情況的影響，設上支座板面積為S，分別取橋跨結構的底面積為S、2S、3S、4S進行計算，結果顯示在橋跨結構厚度達到支座厚度3倍后［6］，底面積大小對支座各部件復合應力計算結果影響較小，為了提高計算效率，取橋跨結構底面積大小與上支座板面積相等，建立球型支座1/2實體模型。

1.4 非線性接觸分析

以有限元模型為基礎，研究球型支座正壓力P、摩擦系數μ、球面曲率半徑R、轉角α等對轉動力矩的影響。有限元分析結果與理論分析結果M=μPR一致，轉動力矩與球面半徑R近似成正比例關系，有限元計算結果與理論值相差1.3%，見圖3。轉動力矩與轉角大小幾乎無關，轉角為0.01～0.04 rad時，轉動力矩為不變值47 kN·m。由此可知，采用大位移非線性有限元分析方法對球型支座轉動性能及結構進行分析是正確合理的。

圖3 球面曲率半徑與轉動力矩關系

2 球型支座轉動時的應力分析

2.1 無轉動時的應力分析結果

在設計載荷作用下，鑄鋼結構最大復合應力遠低于材料的許用應力，最大應力出現在上蓋板處，不會對結構造成破壞。平面四氟板和球面四氟板的復合應力符合聚四氟乙烯材料的許用應力，分布規律為中間應力較小，呈環形往外擴展，應力逐漸增大，最大應力發生在四氟板的邊緣處［6］。

2.2 轉動時的應力分析結果

如圖4為0.02 rad轉角下球型支座復合應力云圖，圖5為0.02 rad轉角下球冠襯板復合應力云圖，圖6為無轉動時球面四氟板復合應力云圖，圖7為0.02 rad轉角下球面四氟板復合應力云圖，圖8，圖9分別為不同轉角下鑄鋼結構和四氟板最大復合應力值。

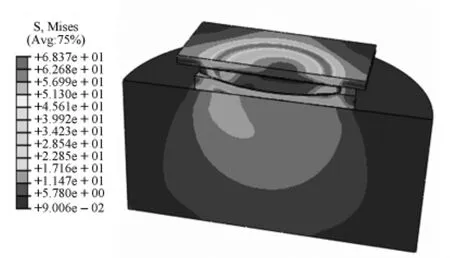
圖4 0.02 rad轉角下球型支座復合應力云圖

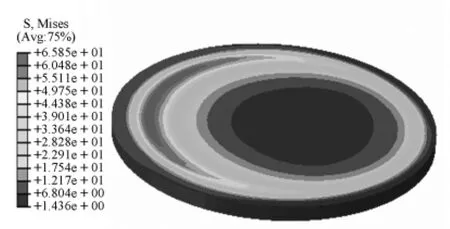
圖5 0.02 rad轉角下球冠襯板復合應力云圖

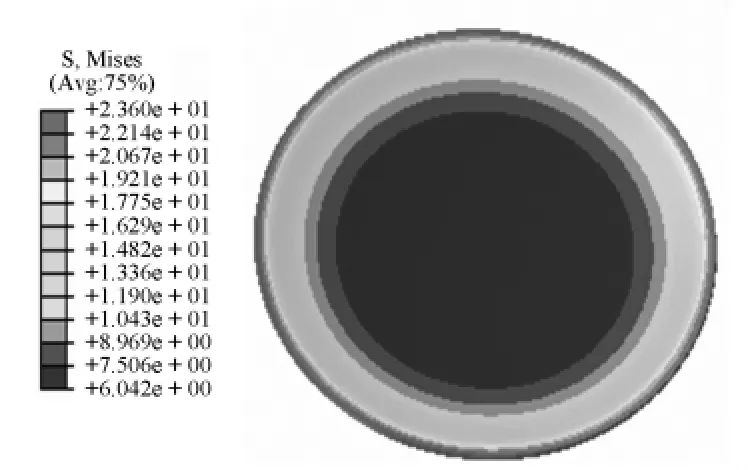
圖6 無轉動時球面四氟板復合應力云圖

圖7 0.02 rad轉角下球面四氟板復合應力云圖

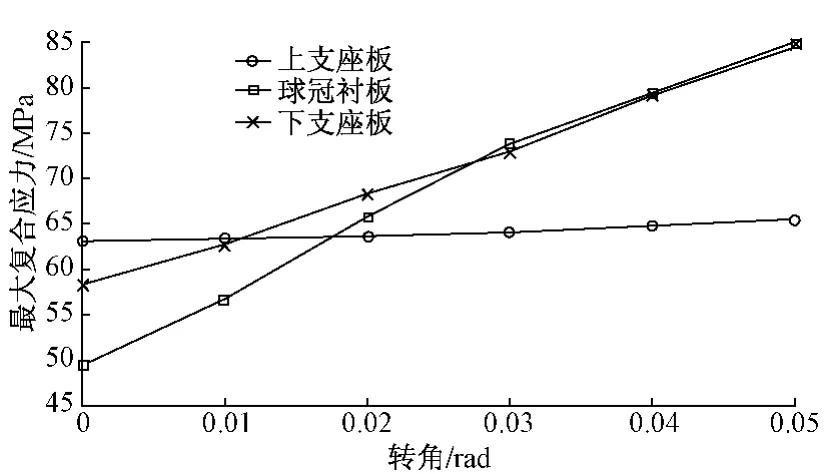
圖8 不同轉角下鑄鋼結構最大復合應力值

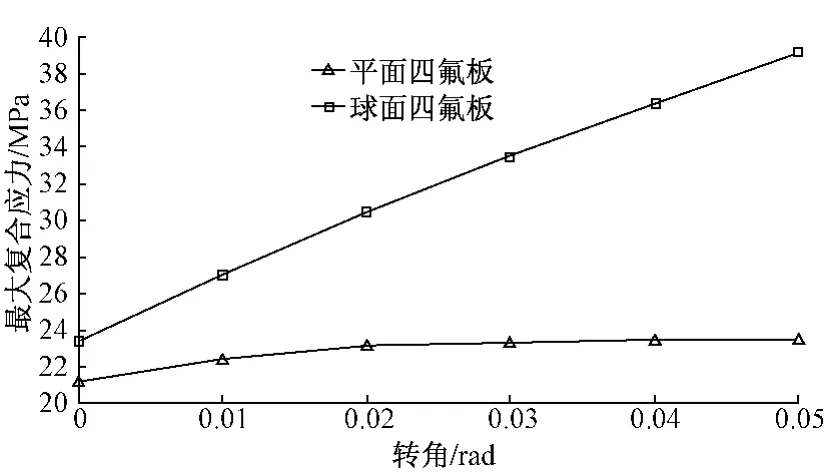
圖9 不同轉角下四氟板最大復合應力值

由圖4和圖5可以看出，當轉角為0.02 rad時，球冠襯板一側端部靠里部分產生了較大復合應力，這是由于支座轉動時該側球冠襯板與球面四氟板接觸面積減小，發生了較大的下撓導致了較大的拉應力。

由圖6和圖7可以看出，當球型支座發生0.02 rad轉動時，球面四氟板最大復合應力值增加了30%，中心處復合應力值變化較小，最大復合應力發生在球面四氟板的一側邊緣處。

由圖8可以看出，隨著轉角的增大，球冠襯板、下支座板最大復合應力有較大增加，上支座板最大復合應力變化較小，但都遠小于鑄鋼材料的許用應力，因此發生轉動時鑄鋼結構的可靠性較高。

由圖9可以看出，隨著轉角的增大，平面四氟板和球面四氟板的最大復合應力均增加，但球面四氟板最大應力增加值遠大于平面四氟板，當轉角達到0.02 rad時，球面四氟板的最大復合應力為30.47 MPa，大于聚四氟乙烯材料的許用應力30.00 MPa。因此設計中應考慮轉動工況下球型支座的應力值，以防止支座可靠性的降低，保證支座的安全。

3 球型支座結構參數變化對支座性能的影響

由上述分析可知，隨著轉角的增大，球型支座各部件應力值均增加，尤其是球面四氟板應力值超出了許用應力，因此對轉動工況下的球型支座進行設計優化具有重要的意義。為充分研究結構參數變化對支座性能的影響，利用非線性接觸分析分別計算了球型支座在0.02 rad轉角下，球面四氟板厚度、球冠襯板厚度、球面曲率半徑對支座各部件最大復合應力值的影響。如圖10為球面四氟板厚度對球面四氟板最大復合應力的影響，圖11為球面曲率半徑對四氟板最大復合應力的影響。

圖10 不同球面四氟板厚度下球面四氟板最大應力值

圖11 不同球面曲率半徑下四氟板最大應力值

分析結果表明，球面四氟板厚度對球面四氟板最大復合應力值影響較大，對其他部件影響較小，由圖10可以看出，隨著厚度的增加球面四氟板最大應力值降低了15.2%，在考慮結構設計要求及成本的前提下，應盡量增大球面四氟板厚度。球冠襯板厚度對支座各部件最大復合應力值影響較小，在滿足結構設計要求前提下，應盡量減小球冠襯板厚度，降低成本。球面曲率半徑對支座最大復合應力影響較大，下支座板、球冠襯板最大復合應力有明顯降低。

由圖11可以看出，隨著球面曲率半徑的增大，平面四氟板最大復合應力增加了9.3%，但仍小于許用應力，球面四氟板最大復合應力值降低了21.6%，平面四氟板和球面四氟板最大復合應力值逐漸接近，便于采用等強度設計法對四氟板進行結構設計，但過大的球面曲率半徑下，球型支座轉動過程中位移量太大，使安全性減低，因此在結構設計合理的前提下，應盡量增大球面曲率半徑。

4 結論

1)采用ABAQUS非線性接觸分析對球型支座轉動力矩進行驗證，分析結果與理論計算一致，有M=μPR，說明采用非線性接觸分析對球型支座進行研究是合理的。

2)轉動情況下，球型支座各部件應力較無轉動工況下有明顯增加，應力值隨轉角的增大而增加，且球面四氟板最大復合應力超過了許用應力，為保證球型支座使用安全，設計中必須考慮轉動工況。

3)在滿足結構設計要求的前提下，增大球面四氟板厚度和球面曲率半徑，可以降低轉動工況下球面四氟板最大復合應力值，使球型支座各部件應力均低于許用應力，改善支座的性能。

［1］ 莊軍生．橋梁支座［M］．北京:中國鐵道出版社，2000．

［2］ 劉岳兵，王少華，王宏謀，等．盆式橡膠支座結構及混凝土墩臺非線性有限元分析［J］．鐵道建筑，2010(9):28-30．

［3］ 劉岳兵，王少華，王宏謀，等．基于ANSYS分析的盆式橡膠支座結構及性能研究［J］．鐵道建筑，2009(10):1-3．

［4］ 中華人民共和國國家標準．GB/T 17955—2009 橋梁球型支座［S］．北京:國家標準管理委員會，2009．

［5］ 莊茁．基于ABAQUS的有限元分析和應用［M］．北京:清華大學出版社，2008．

［6］ 何維．橋梁支座結構分析及疲勞性能研究［D］．成都:西南交通大學，2011．