基于回歸分析的失業預警建模實證研究

李 宏，李建武，莫 榮，宋玉龍

(1.中國人民大學勞動人事學院北京，100872;2.人力資源和社會保障部勞動科學研究所，北京，100029;3.北京理工大學計算機學院智能信息技術北京市重點實驗室，北京100081)

一、引言

失業問題既是綜合性的經濟問題，又是復雜的社會問題。西方發達國家和許多發展中國家，都把實現“充分就業”作為社會經濟發展的重要目標之一。

當前，我國經濟面臨十分復雜的國際經濟環境，人民幣升值、原材料價格上漲、通脹輸入壓力增加等等，導致出口和經濟增速下降、部分小企業倒閉，其可能帶來的失業問題值得關注，政府對此問題也高度重視。如何對失業狀況進行科學預測，根據預測結果適時發出警報，并制定有針對性的預案，對之進行及時有效的調控，是我國在經濟轉軌時期必須認真對待解決的客觀現實問題。

在我國，黨的十六屆三中全會第一次提出，要建立和健全各種預警和應急制度，提高政府應對突發事件和風險的能力。2008年1月1日開始施行的《中華人民共和國就業促進法》第四十二條明確規定:“縣級以上人民政府建立失業預警制度，對可能出現的較大規模的失業，實施預防、調節和控制”。第四十三條規定:“國家建立勞動力調查統計制度和就業登記、失業登記制度，開展勞動力資源和就業、失業狀況調查統計，并公布調查統計結果”。

建立一整套失業監測、預警和預案的體系，對于促進社會穩定與和諧發展，具有重大現實意義。建立失業監測預警系統，完善失業統計和預警制度，掌握勞動力資源和勞動力市場供求狀況，對各級政府制定就業政策，兼顧效益與安定，控制失業規模，保持社會穩定具有重要意義。

二、失業預警研究現狀及存在問題分析

(一)研究現狀

國外失業預警模型主要建立在宏觀經濟預警系統的基礎之上。在20世紀60年代前，西方國家對經濟預警系統的研究停留在經濟循環和經濟晴雨表(Economic Barometer)等預測研究的層面上［1］。1950年 Moore的擴散指數和 1960年Shiskin的綜合指數成為美國構造預警系統的兩大基本方法［1－3］。采用時間序列分析建模是該領域中的一類重要方法，已經取得了豐富的成果，如Jeffrey等人采用的移動平均模型［4］、Enriquede 采用的自回歸模型［5］、Hansen采用的門限自回歸模型［6］、Van Dijk等人采用的基于分數協整與平滑轉換自回歸相結合的模型［7］以及Harvey的時間序列自回歸移動平均模型結合Kalman濾波及季節性調整的技術［8］。Engle于1982年提出了ARCH(AutoRegressive Conditional Heteroskedasticity)類模型［9］，大大改進了預警風險的評估方法。進一步，Bollerslev于1986提出了 GARCH模型(Generalized ARCH)［10］。Kaminsky，Lizondo 與 Reinhart于1997年創建了KLR信號分析法［11］，其基本思想是選擇一系列指標并根據其歷史數據確定其臨界值，當某個指標的臨界值在某個時期被突破，就意味著該指標發出了一個危機信號。

1988年，本文作者所在的勞動科學研究所失業預警課題組首次倡導“勞動部門應建立包括失業預警系統在內的六大勞動預警系統”［12］。經過多年的潛心研究，該課題組于2001年完成“我國失業預警與就業對策研究報告”，該工作以失業率或失業人數作為自變量，使用了數學建模方法和數據庫技術［13］。劉偉等人對深圳市失業預警監測系統進行了研究［14］。首都經貿大學的紀韶教授經過多年的研究，出版了專著《中國失業預警—理論視角、研究模型》［1］。秦開運對構建失業預警系統需要的指標進行了分析［15］，而丁立宏等人對完善我國失業統計指標體系給出了若干建議［16］。劉紅霞從勞動力市場、勞動力構成、經濟發展三維度出發，設計了失業預警指標體系［17］。陳仲常等人采用BP(Back Propagation)神經網絡對我國失業預警系統進行了建模［18］。李永捷通過建立徑向基函數神經網絡模型，對成都市的失業狀況進行了分析與建模［19］。張興會等人則分別采用遞階對角神經網絡［20］與對角 Elman神經網絡模型［21］對失業預測系統進行了建模。向小東等人采用機器學習與模式識別領域中的核技巧，對失業預警系統進行了非線性建模分析，使用支持向量機建立了回歸預測模型［22］。趙建國等人基于擴散指數法與逐步回歸技術改進了失業預警模型，進行了實證分析［2－3］;并對我國現行失業警戒線確定方法進行了探討，構建了基于綜合指數的失業預警模型［23］。黃波等人基于排序logit模型對城鎮就業進行了風險分析及預測［24］。

由上可見，當前國內外學術界已經采用了多種定量分析方法對失業預警系統進行建模，可歸納為兩大類方法:一大類方法是采用基于時間序列分析的計量經濟模型，如自回歸滑動平均模型、ARCH模型等等;另一大類則是采用回歸分析的技術，如線性回歸、各種神經網絡模型等等。同時，這些技術在我國不同的城市或地區得到了初步的嘗試。

(二)存在的問題

盡管我國在失業預警系統研究方面已取得了初步的成就，但仍然存在很大的不足。具體表現為:當前可獲得的與失業預警相關的樣本數據非常有限，是典型的小樣本建模問題;涉及到的社會經濟指標眾多，需要面臨高維數據建模的難題;該系統也包含了復雜的非線性數學模型，通常的線性建模技術并不適用;由于社會經濟調查數據中會存在多種噪音，還可能存在部分調查數據的缺失，進一步加大了失業預警建模的難度。

眾多的社會經濟指標使得失業率的概率分布復雜，很難成為平穩分布，再加上調查中存在的誤差及各種噪音數據的存在，使得傳統的各種時間序列分析模型(如ARCH模型、GARCH模型等)的使用受到了極大的限制。

另外，不同的研究人員分別采用了不同的失業預警建模方法，目前仍然沒有對各種方法進行過系統的比較，很難判斷出各種方法的性能優劣，這給失業預警用戶對不同模型的選擇帶來了困惑。

(三)本文主要工作

在失業預警系統建模中，數據的預處理非常重要。本文首先討論了常用的缺失數據處理機制、數據歸一化方法以及高維數據降維與數據去噪聲技術。

鑒于回歸技術是失業預警建模的重要途徑，本文采用五種回歸技術對失業預警系統進行建模，包括:最小二乘回歸、Logistic回歸、嶺回歸、BP神經網絡以及支持向量回歸。

基于廣東省與失業相關的社會經濟調查數據(2000—2010年)，對上述5種回歸方法進行了實證分析，并根據實驗結果對各種方法的性能進行了比較與評價，旨在為相關部門對失業預警模型的選擇提供參考。

三、失業預警建模的數據預處理技術

(一)失業預警指標選擇

本文作者中的莫榮、李宏于2001年完成了國家科委軟科學研究項目“我國失業預警系統與對策研究”(K97－10－50)，對失業預警所需指標體系進行了系統的分析。本文直接采用其中的指標體系，具體選擇如下的25個宏觀經濟指標作為調查變量:

失業指標1個:城鎮登記失業率;

國民經濟發展指標5個:國內生產總值(GDP)、第一產業生產總值、第二產業生產總值、第三產業生產總值、工業增加值;

勞動力資源指標2個:勞動年齡人口、普通高等學校學生數;

投資指標1個:基本建設投資總額;

能源和材料指標4個:能源生產總量、發電量、鋼產量、水泥產量;

貿易指標4個:商品銷售現金收入、海關統計進出口總額、進口總額、出口總額;

財政貨幣指標4個:金融機構企業存款、市場貨幣流通量、貨幣供給M1、貨幣供給M2;

生活和價格指標4個:銀行工資性現金支出、居民人均收入、居民消費價格總指數、商品銷售價格指數。

(二)常用缺失數據的處理方法

數據缺失是一種在失業預警系統數據采集過程中常見的問題，缺失數據是指由于各種原因本應該得到而實際上沒有得到的數據。

處理缺失數據的方法［25－26］可分為3類:加權方法、填補方法和參數似然方法。

加權方法的本質是將賦予缺失數據的權數分擔到非缺失數據身上。

填補方法的核心問題是為缺失數據尋找一個最佳的“替代值”。填補方法包括傳統的數據填補方法和多重填補方法。傳統數據填補方法包括刪除法、回歸填補法、均值填補法等;常用的多重填補方法包括回歸填補法、預測均值匹配法、Logistic回歸填補法等。

參數似然方法與加權方法和填補方法相比，其處理缺失數據往往能產生更好的估計量，但需要知道數據分布的具體參數模型。

(三)數據的歸一化方法

在失業預警系統建模過程中，所涉及到的各個社會經濟指標數據的量綱往往會存在很大的差異。例如，失業率的統計數值介于0與1之間，而建設投資總額的量度可以達到千萬，城鎮人均收入則以千為單位。如果直接采用各個社會經濟指標的原始數值去建模，各個指標量綱之間的巨大差異會直接影響所建模型的性能。因此，在建模之前，必須對數據進行歸一化處理。

數據的歸一化是通過函數變換將數值映射到某個數值區間，通常把數據歸一化到區間［－1，1］或［0，1］中。常用的歸一化方法［27－28］包括:min －max歸一化方法、零均值歸一化方法、Decimal Scaling歸一化方法、對數函數轉換、反正切函數轉換。

(四)高維數據降維與去噪聲

在失業預警系統建模中，當前可以獲得的數據非常有限。從我國各省統計信息網上公開的社會經濟指標數據來看，很多數據是直接從2000年開始公布的。就以本文對廣東省進行失業預警系統建模為例，該省是我國一個經濟與人口大省，該省統計信息網上也僅僅公開發布了從2000年到目前的大部分社會經濟指標數據，如果我們以季度為時間周期進行建模，所獲得的社會經濟指標數據也只有40多組。另外，與失業預警系統建模相關的社會經濟指標眾多，選出20多個與失業相關性強的社會經濟指標。根據回歸的理論分析，為保證所建預測模型的有效性，建模數據的指標越多，所需要的建模數據也就應該越多。

此外，社會經濟調查數據受客觀環境的限制，存在一定的不精確性或誤差，我們把此稱為數據噪聲。數據中存在的噪聲一定程度上會影響所建失業預警模型的性能。

為此，可以采用主成分分析［29］或獨立成分分析［30］來對所獲得的調查統計數據進行處理。這樣做的原因有兩點:第一、失業預警系統建模中所涉及的各項社會經濟指標之間存在一定的相關性，通過主成分分析或獨立成分分析可以提取這些相關數據中的主要成分或獨立成分，從而達到降維的目的;第二、社會經濟調查統計數據中往往存在數據缺失與各種調查誤差，通過提取主成分或獨立成分，去掉的部分可以認為是調查數據中存在的各種噪聲。

四、回歸分析模型

回歸分析是數理統計學與機器學習研究中的重要內容，近些年來，相關研究成果層出不窮。本文著重探討最小二乘回歸、Logistic回歸、嶺回歸、BP神經網絡以及支持向量回歸等模型。

(一)最小二乘回歸

最小二乘回歸［31］是一種線性回歸模型，線性回歸是使用線性函數從現有的數據中估計出模型中所包含的未知參數的過程，基于所建立的回歸模型可以對未來的數據進行預測。

給定訓練樣本集{xi，yi}，xi∈Rd，i=1，2，…，n，xi=(xi1，xi2，…，xid)T，yi∈R，尋找一個線性函數(常數項作為w的一個維度出現，不再顯式給出，以下均如此)

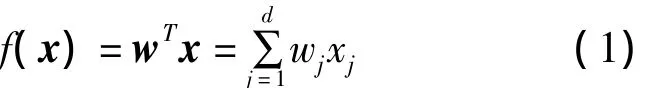
使損失函數L(f(x)，y)達到最小值，即尋找一個最優的向量w使損失函數最小。這里取損失函數為對訓練樣本預測的誤差平方和，即

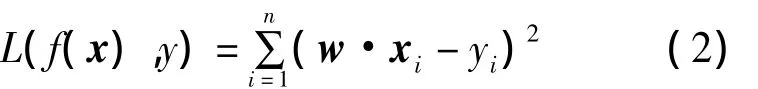
對w求偏導并令其為零，最終可得線性回歸方程為:

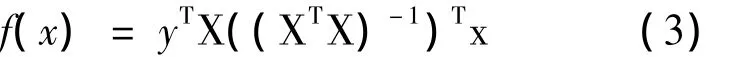
其中，X為n×d矩陣，它的每一行由列向量xi的轉置構成，i=1，2，…，n，w 為 d維列向量，y為 n 維列向量，y=(y1，y2，…，yn)T，x為測試樣本。若XTX不可逆，可以計算XTX的偽逆。

(二)Logistic回歸

Logistic回歸［28］以兩類別標志0與1作為回歸目標，其中一個重要概念就是優勢比(Odds Ratio)，假設Logistic回歸中的一個類別輸出的概率為P，則另一個類別輸出的概率為1－P，則優勢比可以定義為:

用輸出1與0分別表示兩個類別，假設輸出y=1的概率為P，則y=0的概率為1－P，自變量為x，則建立Logistic回歸模型為:

其中，w是接下來要估計的未知參數。假設所有訓練樣本的個數為n，yi是第i個訓練樣本，i=1，2，…，n，服從伯努利分布。用最大似然估計法估計其中的參數w。似然函數為:

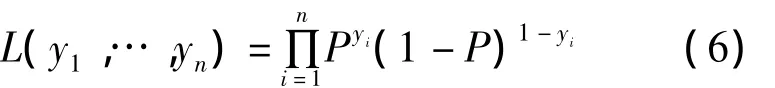
對似然函數取對數，并對w求偏導令其為零，可解出待估參數。

(三)嶺回歸

嶺回歸(Ridge Regression)［32］是對基本的最小二乘回歸的一種改進，最小二乘回歸使用的是傳統的經驗風險最小化原則，而嶺回歸技術采用的是正則化的思想。

對于公式(1)中給出的待求解的線性回歸方程，嶺回歸的目的就是尋找最優的w使得下面的目標函數最小，即

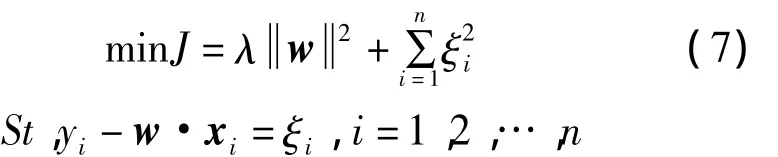
其中，λ為正則項參數，控制著正則化程度，起到平衡兩項的作用。相對應的Lagrange函數為:

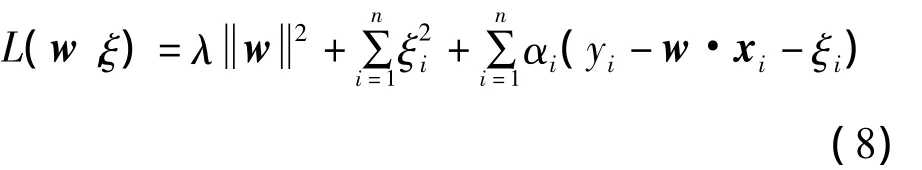
其中，ai為Lagrange乘子。分別對w和ξi求偏導并令等式為零，可以獲得最終的解。

(四)BP神經網絡模型

1986年，David E.Rumelhart等學者提出多層感知器的反向傳播(Backpropogation，簡稱BP)算法，這種學習算法使得多層感知器可以逼近任意復雜的非線性函數。BP學習算法要求激活函數是可微的。BP神經網絡是一種采用BP學習算法的前饋神經網絡，拓撲結構如圖1所示。

圖1 BP神經網絡拓撲結構

BP算法采用梯度下降方法試圖最小化網絡輸出值和期望輸出值之間的誤差平方，詳細計算過程參見文獻［28］。

(五)支持向量回歸

支持向量回歸(Support Vector Regression，簡稱SVR)［33］方法是由Vapnik等人在1996年提出。

假設給定訓練樣本集合{xi，yi}，xi∈Rd，i=1，2，…，n，xi=(xi1，xi2，…，xid)T，yi∈R。尋找最優的w，使回歸函數

對所有的訓練樣本，在ε不敏感損失準則下訓練誤差最小。用約束最優化模型描述該問題為:

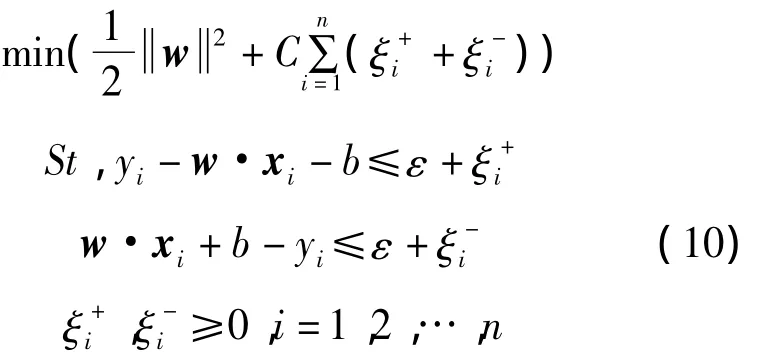
利用上式對應的對偶最優化問題以及KKT條件最終可求得回歸方程為:

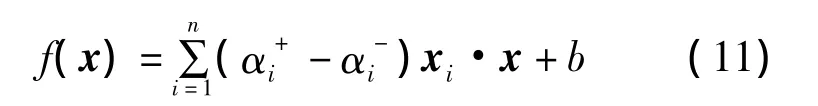
其中，x為新輸入的測試樣本，

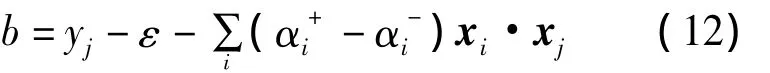
xj為任意一個支持向量。

如果在原空間中的數據不滿足線性關系，可以使用核技巧，將原空間中的樣本映射到一個高維特征空間中，即定義一個核函數K(x，y)，用核函數代替兩個原始向量在特征空間中像的內積，此時，式(11)變為:

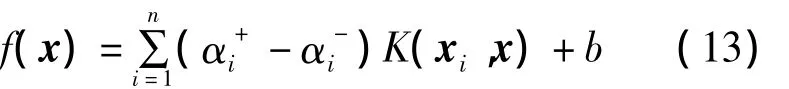
其中，

五、失業預警建模實證研究

廣東省作為外來勞動力輸入的大省，吸納了幾千萬外來勞動力就業。但該省經濟以外向經濟為主，不僅受國際經濟發展的影響很大，而且受到部分國家貿易保護和貿易壁壘的影響也很大，因此，在局部行業、產業和地區將存在造成大規模失業的可能性。因此，在該省建立一整套失業監測與預警體系，具有重大的現實意義。

(一)數據預處理

1.失業基準指標

預測失業的變化，失業基準指標的選擇是非常重要的環節，在這里直接采用城鎮登記失業率作為基準指標。

2.數據來源和預處理

城鎮登記失業率數據來自于廣東省人力資源和社會保障廳失業保障處。我們從該省統計信息網得到2000年第1季度到2010年第3季度的17個經濟指標的季度或月度數據(前面部分提到了除失業率外的24個社會經濟指標數據，但剩余的7個指標數據難以獲得)，分別為:生產總值(GDP)、第一產業生產總值、第二產業生產總值、第三產業生產總值、工業增加值、單位從業人員、建設投資總額、能源生產總量、發電量、鋼產量、水泥產量、進出口總額、進口總額、出口總額、城鎮單位職工平均工資、居民消費價格總指數和商品零售價格指數。其中居民消費價格總指數和商品零售價格指數指標體系要求提供季度資料，但只查閱到月度資料，對于這兩個指標，我們對其每個季度三個月的數據求均值得到季度數據。此外居民消費價格總指數2006年至2008年的數據以及商品零售價格指數2003年至2008年的數據來源于國家統計數據庫。其余的月度數據，我們直接求該季度所包含的月度數據的和得到季度數據。用每個季度的經濟指標加上城鎮登記失業率作為行向量，這樣可以構成43×18的矩陣。

由于統計數據存在缺失，在此統一采用均值填補法進行填補。

處理完缺失數據后，由于各個經濟指標的單位不統一，需要對數據進行歸一化處理。在此采用零均值歸一化方法，即采用下面公式:

其中，x、y分別為轉換前和轉換后的值，ā是屬性A原始值的均值，σA是屬性A原始值的標準差。

由于采集到的數據較少，而每組數據的指標眾多，同時考慮到社會經濟數據調查中存在一定的噪聲以及缺失數據，因此接下來對數據進行主成分分析，對數據進行降維與去噪聲。首先我們去掉城鎮登記失業率數據，將數據變成43×17的矩陣。我們取2000年第1季度的數據到2008年第3季度的數據作為訓練樣本集，取2008年第4季度的數據到2010年第3季度的數據作為測試樣本。然后對訓練樣本進行主成分分析，設置貢獻率閾值為95%，即至少保持原始數據的95%的信息。經過處理后，將原來的17維數據降到4維，原始數據的協方差矩陣最大的4個特征值為

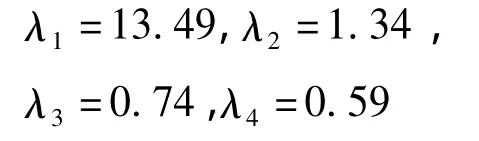
最后對訓練樣本和測試樣本進行降維，將它們投影到由這4個特征向量張成的子空間中，這樣就得到了降維后的數據。

(二)實驗結果

1.構造訓練樣本集和測試樣本集

數據經過預處理之后，用本季度的經濟指標加上當前季度之前三個季度的失業率和本季度失業率來對下一個季度的失業率進行預測，故樣本集可表示為

＜Xi，Yi＞ = ＜ 本季度的經濟指標 +前三個季度的失業率 +本季度的失業率，下一季度的失業率＞

取2000年第1季度到2008年第4季度的數據作為訓練樣本集，取2009年第1季度到2010年第3季度的數據作為測試樣本集，根據所計算的預測結果與實際調查數據來統計預測精度。

2.最小二乘回歸實驗結果

失業率的最小二乘回歸模型如下

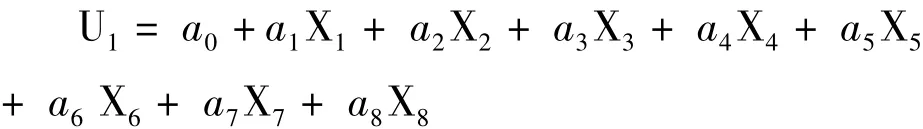
其中，ai為所求系數，i=0，2，…，8;U1代表失業率;Xi代表影響失業的各種經濟因素(此處為經過主成分提取后得到的降維數據)，i=1，2，3，4，Xj為當前季度之前三個季度的失業率，j=5，6，7，X8代表當前季度的失業率。

根據最小二乘回歸算法，得到失業率模型的參數，列在表1中。

圖2展示了2009年第1季度到2010年第3季度失業率的預測值與真實值的比較，其中橫坐標軸給出的是從2009年第1季度到2010年第3季度的時間跨度，分別對應了數值1～7，以下各圖坐標軸的含義相同，不再重復說明。

3.Logistic回歸模型實驗結果

失業率的Logistic回歸模型如下:

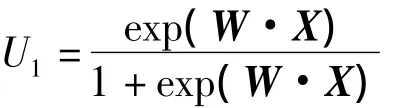
其中，U1為失業率，

W=(w1，w2，w3，w4，w5，w6，w7，w8)，為待估參數，

X=(X1，X2，X3，X4，X5，X6，X7，X8)，Xi代表影響失業的各種經濟因素(此處為經過主成分提取后得到的降維數據)，i=1，2，3，4，Xj為前三個季度的失業率，j=5，6，7，X8代表當前季度的失業率。

經過計算，得到失業率模型的待估參數值，見表2。

表1 基于最小二乘回歸的失業率模型參數值

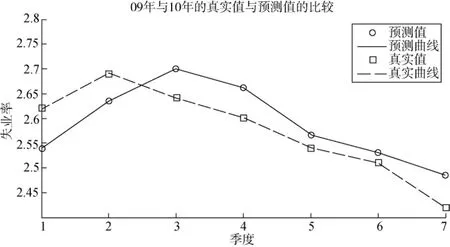
圖2 基于最小二乘回歸的失業率模型真實值與預測值比較

表2 基于Logistic回歸的失業率模型的參數值

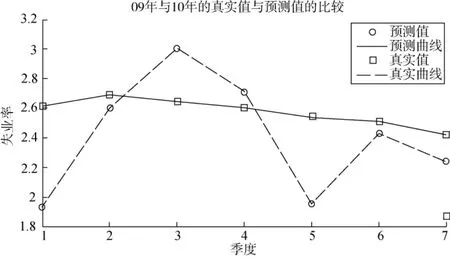
圖3 基于Logistic回歸的失業率預測值和真實值的比較

表3 基于嶺回歸的失業率模型的參數值

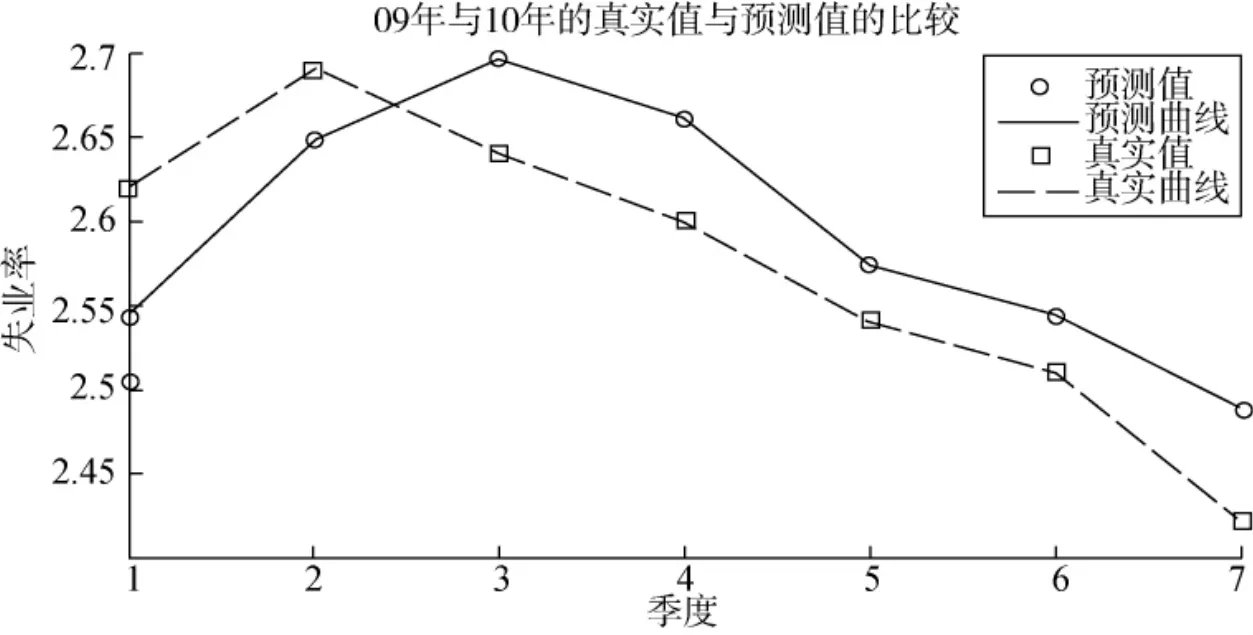
圖4 基于嶺回歸的失業率模型的真實值與預測值比較

圖3為2009年第1季度到2010年第3季度失業率的預測值與真實值的比較。

4.嶺回歸模型實驗結果

失業率的嶺回歸模型如下:

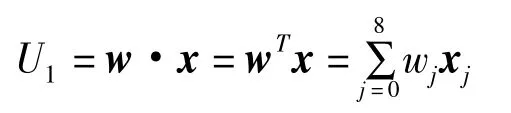
其中，U1為失業率，

W=(w0，w1，w2，w3，w4，w5，w6，w7，w8)，為待估參數，

X=(1，X1，X2，X3，X4，X5，X6，X7，X8)，Xi代表影響失業的各種經濟因素(此處為經過主成分提取后得到的降維數據)，i=1，2，3，4，Xj為前三個季度的失業率，j=5，6，7，X8代表當前季度的失業率。

根據嶺回歸算法，得到待估系數值，見表3。

圖4為2009年第1季度到2010年第3季度失業率的預測值與真實值的比較。

5.BP神經網絡回歸模型實驗結果

根據BP神經網絡，得到2009年第1季度到2010年第3季度失業率的預測值與真實值的比較，見圖5。

6.支持向量回歸模型實驗結果

支持向量回歸模型采用2階多項式核函數。

根據支持向量回歸算法，我們得到2009年第1季度到2010年第3季度失業率的預測值與真實值的比較，見圖6。

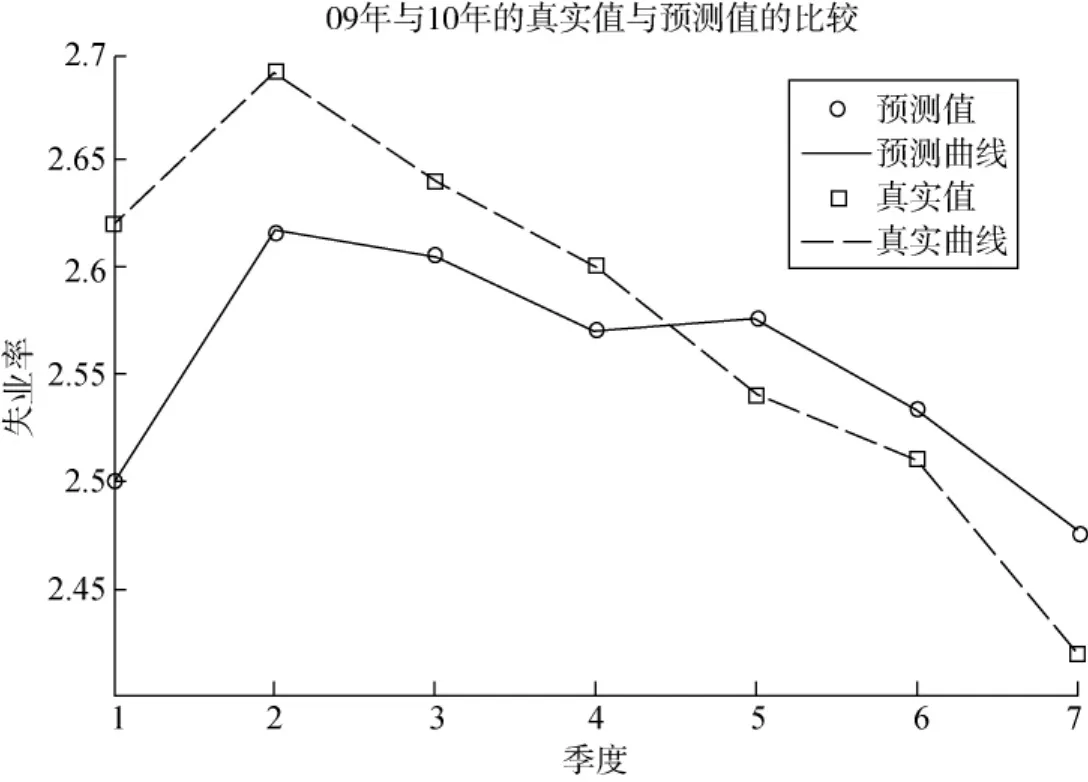
圖5 基于BP神經網絡模型的失業率真實值與預測值比較

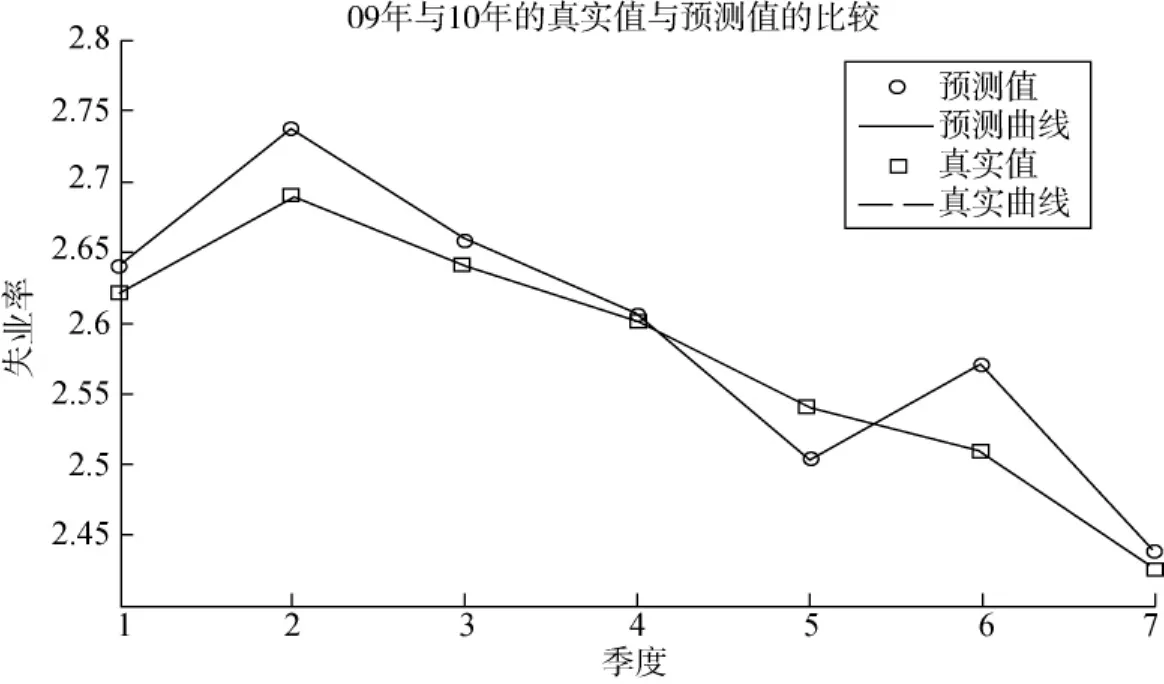
圖6 基于支持向量回歸的失業率真實值與預測值比較

(三)實驗結果對比分析

我們對上述失業率回歸模型的均方誤差和相對誤差進行比較，列在表4中。

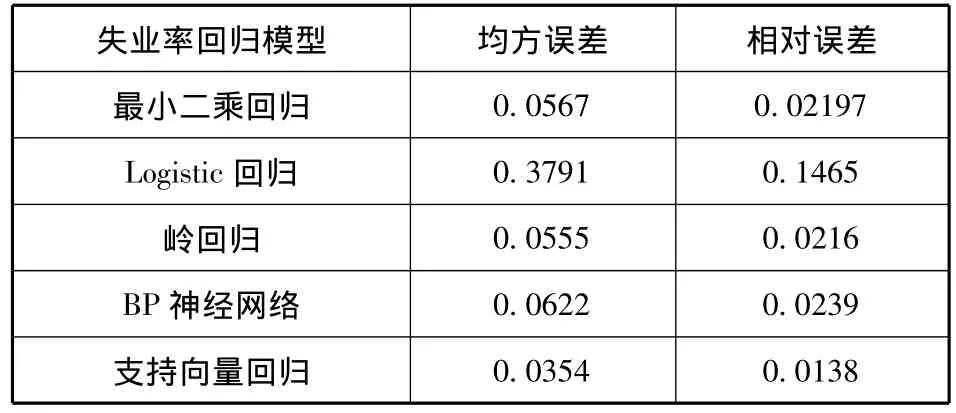
表4 失業率回歸模型的均方誤差和相對誤差比較

根據均方誤差、相對誤差以及前面各個圖形可知:Logistic回歸模型對失業率的預測效果最差，支持向量回歸模型對失業率的預測效果最好，最小二乘回歸、嶺回歸和BP神經網絡模型的預測效果介于Logistic回歸與支持向量回歸之間。

由于BP神經網絡的性能受隨機初始值的影響較大，導致結果不穩定且可能陷入局部極小點。由于支持向量回歸只采用了二階多項式核函數，就能夠得到相比于其他回歸方法較好的效果，如果采用精細設計的核函數(如多核設計)，支持向量回歸有望得到更好的失業率預測效果。

另外，我們也基于獨立成分分析對原始數據提取獨立成分，并對多種回歸分析模型進行了相應的建模，得到了與采用主成分分析方法相當的計算結果，由于文章篇幅有限，在此不再對該部分實驗結果詳述。

六、結論

本文對基于回歸分析的失業預警建模過程進行了系統分析，包括缺失數據的處理、數據的歸一化、高維數據的降維與去噪聲、回歸分析模型等環節，最終基于廣東省的社會經濟調查數據對五種回歸模型的失業率預測效果進行了綜合比較。實驗結果發現:(1)主成分分析能夠有效地對高維的調查數據進行維數;(2)采用回歸技術可以對失業率發展趨勢進行一定程度的預測;(3)在五種回歸分析模型中，支持向量回歸模型預測效果最好，Logistic回歸模型預測性能最差，最小二乘回歸、嶺回歸和BP神經網絡的預測精度介于Logistic回歸與支持向量回歸的預測精度之間。

下一步的工作將基于集成學習技術對多個回歸模型進行集成，把每個單獨的回歸函數看作為一個專家，把多個專家的預測結果綜合到一起有望獲得更好的預測效果。

［1］紀 韶.中國失業預警—理論視角、研究模型［M］.北京:首都經濟貿易大學出版社，2008.

［2］趙建國，苗 莉.基于擴散指數的逐步回歸改進失業預警模型及實證分析［J］.中國人口科學，2008(5):52－57.

［3］趙建國.基于擴散指數法的失業預警模型及實證分析［J］.財經問題研究，2005(11):81－84.

［4］Jeffrey L R，Tang K.Simple Rules for Combining Forecasts:Some Empirical Results［J］.Socio － Economic Planning Sciences，1987，21(4):239 －243.

［5］Enriquede A.Constrained Forecasting in Autoregressive Time Series Models:A Bayesian Analysis［J］.International Journal of Forecasting，1993，9(1):95 －108.

［6］Hansen B E.Inference in TAR Models［J］.Studies Nonlinear Dynamics Econometrics，1997，2:1 －14.

［7］Van Dijk D，Franses PHPaap R.A Nonlinear Long Memory Model with an Application to US Unemployment［J］，Journal of Econometrics，2002，110:135 －165.

［8］Harvey A C.Forecasting Structural Time Series Models and the Kalman Filter［M］.Cambridge:Cambridge University Press，1989.

［9］Robert F Engle.Autoregressive Conditional Heteroscedasticity with Estimates of Variance of United Kingdom Inflation［J］.Econometrica，1982，50:987 －1008.

［10］Tim Bollerslev.Generalized Autoregressive Conditional Heteroskedasticity［J］.Journal of Econometrics，1986，31:307－327.

［11］Kaminsky，Lizondo，Reinhart.Leading Indicators of Currency Crises［Z］.IMF Working Paper，1997:97 － 99.

［12］莫 榮.2003－2004年:中國就業報告［M］.北京:中國勞動社會保障出版社，2004.

［13］勞動和社會保障部勞動科學研究所課題組.我國失業預警系統與就業對策研究［J］.經濟研究參考，2002，(34):11－26.

［14］劉 偉，陸 華.深圳市失業監測預警系統的研究［J］.數量經濟技術經濟研究，2001(2):106－109.

［15］秦開運.我國失業保障監測預警指標體系的構建［J］.統計與決策，2007(21):81 －82.

［16］丁立宏，王 靜.完善我國失業統計指標體系的構想［J］.經濟與管理研究，2009(7):15－20.

［17］劉紅霞.失業風險預警模型構建研究［J］.現代財經，2008，28(11):28 －32.

［18］陳仲常，吳永球.失業風險預警系統研究［J］.當代財經，2008(5):5－10.

［19］李永捷.基于RBF網絡的成都市失業預警模型［J］.湖南醫科大學學報:社會科學版，2007，9(4):159－162.

［20］張興會，李 翔，陳增強，袁著祉.基于遞階對角神經網絡的失業預測研究［J］.數量經濟技術經濟研究，2002，19(9):114－117.

［21］張興會，杜升之，陳增強，袁著祉，莫 榮.基于對角Elman神經網絡的失業預測模型［J］.南開大學學報:自然科學，2002，35(2):60 －64.

［22］向小東，宋 芳.基于核主成分與加權支持向量機的福建省城鎮登記失業率預測［J］.系統工程理論與實踐，2009，29(1):73 －80.

［23］趙建國.綜合失業警戒指數的構建及其失業警報分析［J］.財經問題研究，2009(7):94－98.

［24］黃 波，王楚明.基于排序logit模型的城鎮就業風險分析與預測——兼論金融信用危機情形下促進我國就業的應對措施［J］.中國軟科學2010，(4):146－154.

［25］Little RJA，Rubin DB.Statistical Analysis with Missing Data［M］.New York:John Wiley and Sons，2002.

［26］Allison P D.Missing Data［M］.Thousand Oaks，Cali:Sage Publications，2002.

［27］Jiawei Han，Micheline Kamber，Jian Pei.Data Mining:Concepts and Techniques［M］.2nd Edition.Elsevier:Morgan Kaufmann，2006.

［28］Christopher M.Bishop.Pattern Recognition and Machine Learning［M］.Berlin:Springer，2006.

［29］JOLLIFFE IT.Principal Component Analysis［M］.Lnd ed.New York:Springer－ Verlag，2002.

［30］Pierre Comon.Independent Component Analysis:A New concept?［J］.Signal Processing，1994，36(3):287 －314.

［31］Kutner M H.Applied Linear Regression Models［M］.4th ed.McGraw － Hill，2004.

［32］Arthur E Hoerl，Robert W Kennard.Ridge Regression:Applications to Nonorthogonal Problems［J］.Technometrics，1970，12(1):69 －82.

［33］Vladimir N.Vapnik.Statistical Learning Theory［M］.New York:John Wiley ＆ Sons，1998.