基于高頻數據的賦權已實現極差β估計量的構建

郭名媛

0 引言

Markowitz提出的現代證券組合投資理論運用數理統計的方法全面而細致地分析了何為最優的資產結構和如何選擇最優的資產結構。一般而言，投資風險越大，其期望收益也就越高。投資者在權衡收益和風險時，以其對投資風險的偏好來進行證券資產的選擇。資本資產定價模型(CAPM)與Markowitz的現代證券組合投資理論有著極其密切的關系。對于投資者來說，有效投資組合中單個證券的總風險中只有系統風險這部分對有效投資組合的風險做出貢獻，每個證券的非系統風險則在有效投資組合中消失。而資本資產定價模型中的β數則用來衡量有效投資組合中單個證券的風險。資本資產定價模型(CAPM)是以市場收益作為影響因子的單因子模型，具有簡便、易于操作的特點。雖然CAPM也遭到了某些批評，然而對于CAPM的理論研究和實際應用仍然十分的活躍，也證明了其有很大的實用價值。國內對資本資產定價模型的研究主要始于20世紀90年代，雖然CAPM在中國股票市場的適用性是一個問題。但是，它所包含的基于Markowitz的資產組合理論，它對風險的分析，對市場組合及其替代物的論述以及它對風險與收益之間關系的描述，對中國的股票市場有很大的指導意義。充分利用CAPM較強的邏輯性、實用性，通過對股票市場的實證分析和理論研究，有利于發現問題，推動我國股市的發展。因此，正確確定CAPM中的系統風險系數β非常重要。

大多數國內外的實證研究證明了系統風險系數β是可變的，投資者的風險厭惡程度與經濟所處的狀態相關，在股票市場的不同的時期，股票的系統風險系數β會有所變化。De Santis,Gerard(1997)[1]證明系統風險系數β隨時間的改變而改變。Bekaert,Harvey(1995)[2]在檢驗世界金融市場之間的協同性的同時，發現系統風險系數β隨著國內和世界的信息變量的改變而改變。Fabozzi，Frank(1977)[3]研究了在不同市場態勢下證券β值的差異及穩定性，并指出當市場狀況從牛市轉向熊市時，β值較不穩定。然而國內外的實證研究主要是采用低頻數據進行的[1～12]。

隨著計算機技術和通訊技術的進步，采集和存儲高頻金融數據已經成為了可能。這使得采用高頻數據來度量系統風險系數β成為了可能。這種方法相對于采用低頻數據更能夠充分利用股票數據的日內信息。

本文擬采用高頻金融數據，通過賦權已實現極差方差和賦權已實現極差協方差來度量市場收益的方差和股票收益與市場收益的協方差，構建賦權已實現極差β估計量，對系統風險系數β進行研究。

1 已實現極差方差和已實現極差協方差

1.1 已實現極差方差

Christensen和Podolskij[13]提出了基于高頻數據的已實現極差方差估計量。采用已實現極差方差來估計金融資產收益的方差，其優點在于這種方法能夠充分利用高頻數據的日內信息，計算簡便。

其中，T為研究跨度天數，N為在[t-1,t]時間段內等時間間隔的采樣次數。Δ=1/N，Δ為將[t-1,t]時間段分為N個時間段的時間間隔。 pi,t,m為金融資產i在第t日的[n-1,n]時間段內的價格。

定義1[13]已實現極差方差（Realized Range-based Variance，簡稱RRV）為:Christensen and Podolskij[13]證明了：

1.2 已實現極差協方差

定義2已實現極差協方差（Realized Range-based Covariance）為金融資產日內極差收益乘積之和，即

2 賦權已實現極差方差和賦權已實現極差協方差

2.1 賦權已實現極差方差

唐勇，張世英[14]在已實現極差方差的基礎上，提出了賦權已實現極差方差。

定義3[14]賦權已實現極差方差（Weighted Realized Range-based Volatility,WRRV）為金融資產i的日內極差收益平方的加權之和，即

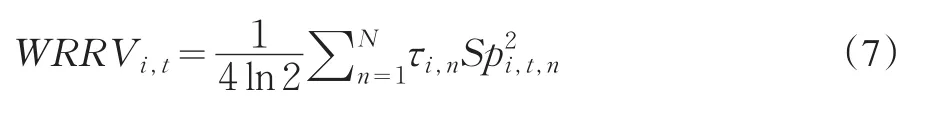
其中：τi,n為日內收益平方的權重。

從賦權已實現極差方差定義中，可以看到當τi,n=1(n=1，…，N)時，WRRVi,t=RRVi,t。即已實現極差方差是賦權已實現極差方差的一個特例。

賦權已實現極差方差中權重確定的計算公式為[14]：

賦權已實現極差方差相對于已實現極差方差具有充分考慮了“日歷效應”，并且比已實現極差方差的方差更小的優點。唐勇，張世英在文獻[14]中對此做出了詳細闡述。

2.2 賦權已實現極差協方差

本文在已實現極差協方差的基礎上，提出了賦權已實現極差協方差。

定義4賦權已實現極差協方差（Weighted Realized Range-based Covariance,WRRCOV）為金融資產i和金融資產 j的日內極差收益乘積的加權之和，即

其中，τij,n為日內極差收益乘積的權重；i,j=1,2,…。

從賦權已實現極差協方差定義中，可以看到當τij,n=1(n=1，…，N）時，WRRCOVij,t=RRCOVij,t。換句話說，已實現極差協方差是賦權已實現極差協方差的一個特例。

2.3 賦權已實現極差協方差中權重的確定

無偏性是對一個估計量最重要的要求之一，要想更好的估計金融資產收益之間的協方差，賦權已實現極差協方差首先需要滿足無偏性。但是，僅僅滿足無偏性是不夠的。因為無偏性只能保證估計量的期望等于真值，它取的值很可能大部分與真值相差很大。因此為了保證賦權已實現極差協方差的取值能集中在金融收益之間的協方差真值附近，還需要確定一個最優的權重以使得賦權已實現極差協方差的方差最小。

（1）賦權已實現極差協方差的無偏性

設：

因

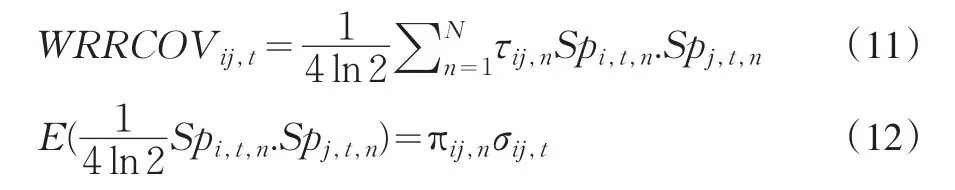
故

由估計量的無偏性可知，要求WRRCOVij,t滿足無偏性，則下式成立：

（2）賦權已實現極差協方差的最小方差性

因

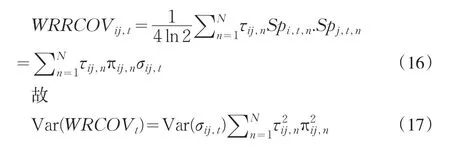
為了使WRRCOVij,t既滿足無偏性，又滿足最小方差性，則：

定義：

其中：θ為拉格朗日乘子。

令：

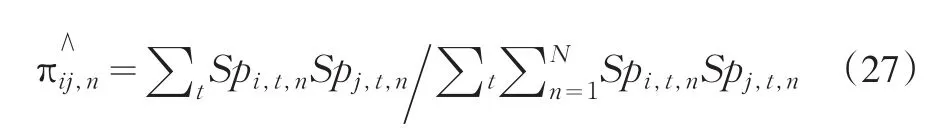
故

因此賦權已實現極差協方差中權重為：

2.4 賦權已實現極差協方差相對于已實現極差協方差的優點

2.4.1 充分考慮了“日歷效應”

“日歷效應”是對高頻金融時間序列的研究中的重要發現。所謂“日歷效應”是指金融資產收益在日內表現出穩定的、周期性的運動模式，主要表現為“U”型模式。

已實現極差協方差是金融資產日內極差收益乘積之和，給每一個日內極差收益乘積都賦予了取值為1的相同的權重。但是，由于“日歷效應”的存在，給不同的日內極差收益乘積賦予相同的權重顯然不太合理。

而賦權已實現極差協方差是金融資產日內極差收益乘積的加權之和，它給不同的日內極差收益乘積賦予了不同的權重。也就是說，根據不同的日內極差收益乘積在日內表現的出穩定的、周期性的運動模式，相應地給每一個日內極差收益乘積都賦予了不同的權重，考慮到了“日歷效應”。正因為考慮了“日歷效應”，給每一個日內極差收益乘積都賦予了不同的權重，才使得賦權已實現極差協方差是既滿足無偏性，又滿足最小方差性的協方差估計量。

2.4.2 賦權已實現極差協方差的方差小于已實現極差協方差的方差

從賦權已實現極差協方差定義中，可以看到當τij,n=1(n=1，…，N）時，WRRCOVij,t=RRCOVij,t。也就是說已實現極差協方差是賦權已實現極差協方差的一個特例。

3 賦權已實現極差β

采用高頻數據,用賦權已實現極差方差和賦權已實現極差協方差來度量市場組合收益的方差和某支股票收益與市場組合收益的協方差。由此便可以計算出賦權已實現極差β。

定義5市場組合收益的賦權已實現極差方差為

第i支股票收益與市場組合收益的賦權已實現極差協方差

第i支股票的賦權已實現系統風險系數

由2.1部分可知，賦權已實現極差方差和賦權已實現極差協方差充分考慮了日歷效應，并且滿足估計量的最小方差性。由此可見，賦權已實現極差β比采用已實現極差方差和已實現極差協方差計算的已實現極差β更精確。

4 實證分析

本文的實證研究采用的高頻數據是2001-2-28～2002-4-15深證成指和晨鳴紙業、金路集團、海虹控股、冀東水泥、鹽湖鉀肥的30分鐘間隔時段的收盤價，這期間共有269個交易日。

4.1 深證成指收益的已實現極差方差和賦權已實現極差方差的統計特征

根據式（4）和式（7），可以計算出深證成指收益的已實現極差方差和賦權已實現極差。表1給出了深證成指收益的已實現極差方差和賦權已實現極差的統計特征。

從表1中可以看到，深證成指收益的已實現極差方差和賦權已實現極差的均值相同，但是深證成指收益的賦權已實現極差的方差要小于已實現極差方差的方差。

表1 深證成指收益的已實現極差方差和賦權已實現極差的統計特征

4.2 各支股票收益與深證成指收益的已實現極差協方差和賦權已實現極差協方差的特性統計

根據式（6）和式（9），可以計算出各支股票收益與深證成指收益的已實現極差協方差和賦權已實現極差協方差。表2各支股票收益與深證成指收益的已實現極差協方差和賦權已實現極差協方差的統計特征。

表2 各支股票收益與深證成指收益的已實現極差協方差和賦權已實現極差協方差的統計特征

從表2中可以看到，各支股票收益與深證成指收益的已實現極差協方差和賦權已實現極差協方差的均值相同，但是各支股票收益與深證成指收益的賦權已實現極差協方差的方差小于等于已實現極差協方差的方差。

4.3 各支股票的賦權已實現極差β的特性統計

表3給出了各支股票的賦權已實現極差β的特性統計結果。從表1中可以看到，各支股票的賦權已實現極差β都具有較高的偏度和峰度，其分布均不符合正態分布。

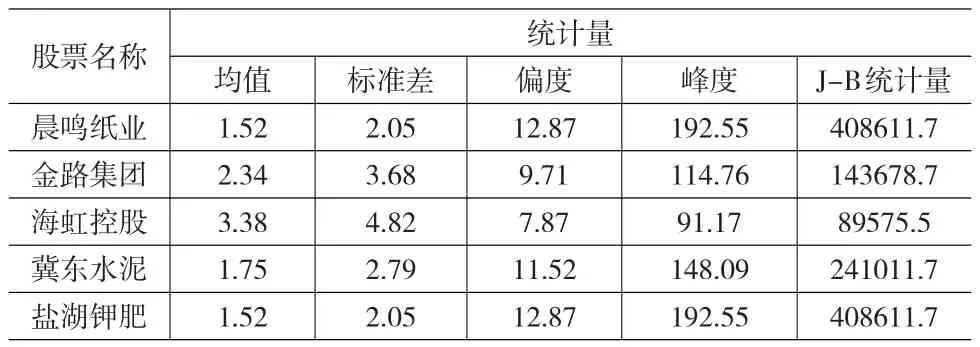
表3 各支股票的賦權已實現極差β的特性統計

5 結束語

本文采用高頻金融數據，通過賦權已實現極差方差和賦權已實現極差協方差來度量市場收益的方差和股票收益與市場收益的協方差，構建了賦權已實現極差β估計量，對系統風險系數β進行了研究。實證研究證明，中國股票市場中的系統風險系數β隨著時間的改變而改變具有較高的偏度和峰度，其分布均不符合正態分布。

[1] De Santis,Gerard.International Asset Pricing and Portfolio Diversifi?cation with Time-varying Risk[J].Journal of Finance,1997,(52).

[2] Bekaert G.,Harvey C.Time-varying World Market Integration[J].Jour?nal of Finance,1995,(50).

[3] Fabozzi,Frank,Francis,Clark.Stability Test for Alphas and Betas Over Bull and Bear Market Conditions[J].Journal of Finance,1977,(9).

[4] Christensen,K.,M.Podolskij.Asymptotic Theory for Range-based Es?timation of Integrated Variance of a Continuous Semi-martingale[R].Aarhus School of Business,2005.

[5] 唐勇,張世英.高頻數據的加權已實現極差波動及其實證分析[J].系統工程,2006,24(8).