基于響應面法的永磁同步電動機磁鋼結構的優化
史朝暉
(山東勝利職業學院,山東東營257097)
0引 言
永磁同步電動機自身優點突出[1-2],其轉矩脈動是影響輸出力矩精度的主要原因之一,影響轉矩脈動的因素主要有繞組反電勢為非理想正弦波導致的轉矩脈動以及齒槽效應引起的轉矩脈動。其中電機氣隙磁密正弦性的好壞是導致反電勢波形不理想的主要因素之一[3],而氣隙磁密與電機轉子永磁體(即磁鋼)密切相關,因此電機磁鋼的優化設計至關重要[4]。
響應面法源于20世紀70年代,用于多變量問題的建模和分析[5]。該方法的核心是根據系統在一系列采樣點上的響應,利用一定的基函數構造輸入輸出關系解析式,然后求其最優點。響應面法在化學和生物領域已得到了廣泛的應用,主要目的是實現過程和結構的優化[6],卻較少應用于電機領域中,文獻[7]將響應面法應用于基于磁路分析的永磁直流微電機堵轉轉矩的優化設計。文獻[8]則將響應面法用于雙定子永磁同步發電機中提高了永磁電機的設計效率。
本文以永磁同步電動機為例,采用響應面法,對永磁同步電動機的磁鋼進行設計,給出了基于響應面法的設計變量、目標函數及具體的響應面法設計過程,并采用遺傳算法對響應面函數進行最優點求解,進而得到了磁鋼的最優設計方案。
1永磁同步電動機結構
永磁同步電動機結構示意圖如圖1所示,主要結構參數如表1所示。
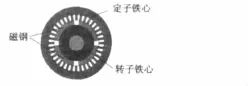
圖1 永磁同步電動機結構示意圖

表1 電機主要設計參數
由于永磁同步電動機的氣隙磁密要求為正弦波,因此氣隙磁場的正弦畸變率對于永磁同步電動機而言至關重要。本文將響應面法用于永磁同步電動機的氣隙磁密的優化之中,下面進行詳細分析。
2基于響應面法的磁鋼優化設計
2.1響應面法簡介
響應面法是一種根據已有的采樣點及對采樣點評價值來構建逼近實際中不可能用準確表達式表示的函數的方法。
設 Xi(i=1,2,…,N)為 N 個實驗樣本點,fi(i=1,2,…,N)為對應于 N個實驗樣本點的目標函數值。下面是響應面函數構建的具體過程:
(1)首先計算形狀參數h:
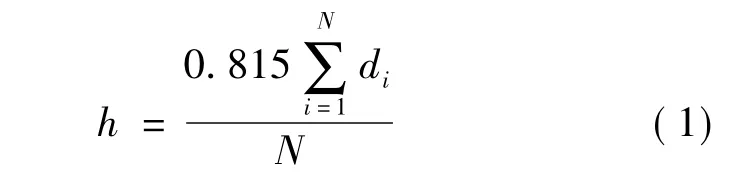
式中:di為第i個采樣點與當前樣本點組中距其最近的采樣點之間的距離。
(2)求取響應面函數系數cj:
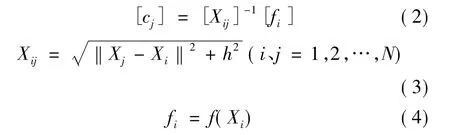
式中:h為形狀參數,它決定了重構函數的曲率。
(3)得到響應面函數:
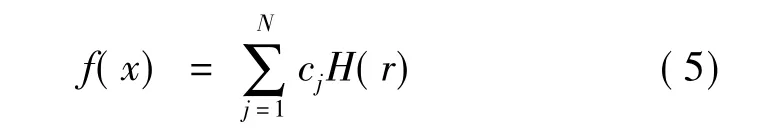
式中:H(r)=H(‖X-Xj‖),H(r)為徑向基函數,其表達式:
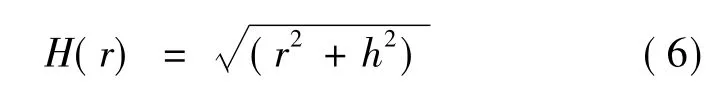
2.2采用響應面法的磁鋼優化設計
本文通過優化磁鋼極弧形狀,如圖2所示,以得到一個更接近于正弦的氣隙徑向磁密,進而使繞組中反電動勢更加接近于正弦波。
選取磁鋼外圓弧的半徑R及磁鋼極弧系數θ為優化變量。
變量范圍:外圓弧半徑 R=OA=[0,20],永磁體的極弧系數θ=α/90=[0.8,1]。所選取的第一組采樣點及采樣點對應并通過有限元方法計算所得的氣隙磁密波形畸變率,如表2所示。
響應面方法中有最重要的三類中心復合設計:外切中心復合設計(CCC)、嵌套中心復合設計(CCI)和面心立方設計(CCF),本文中選取的是外切中心復合設計(CCC)。
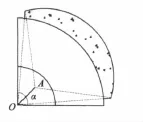
圖2 磁鋼結構示意圖

表2 優化變量與波形畸變率
初始樣本點組的分布如圖3所示。
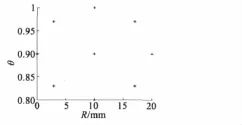
圖3 初始樣本點分布
由式(1)~(6)可以得到:
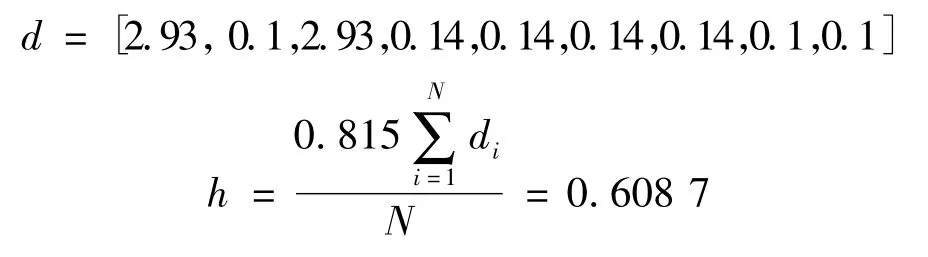
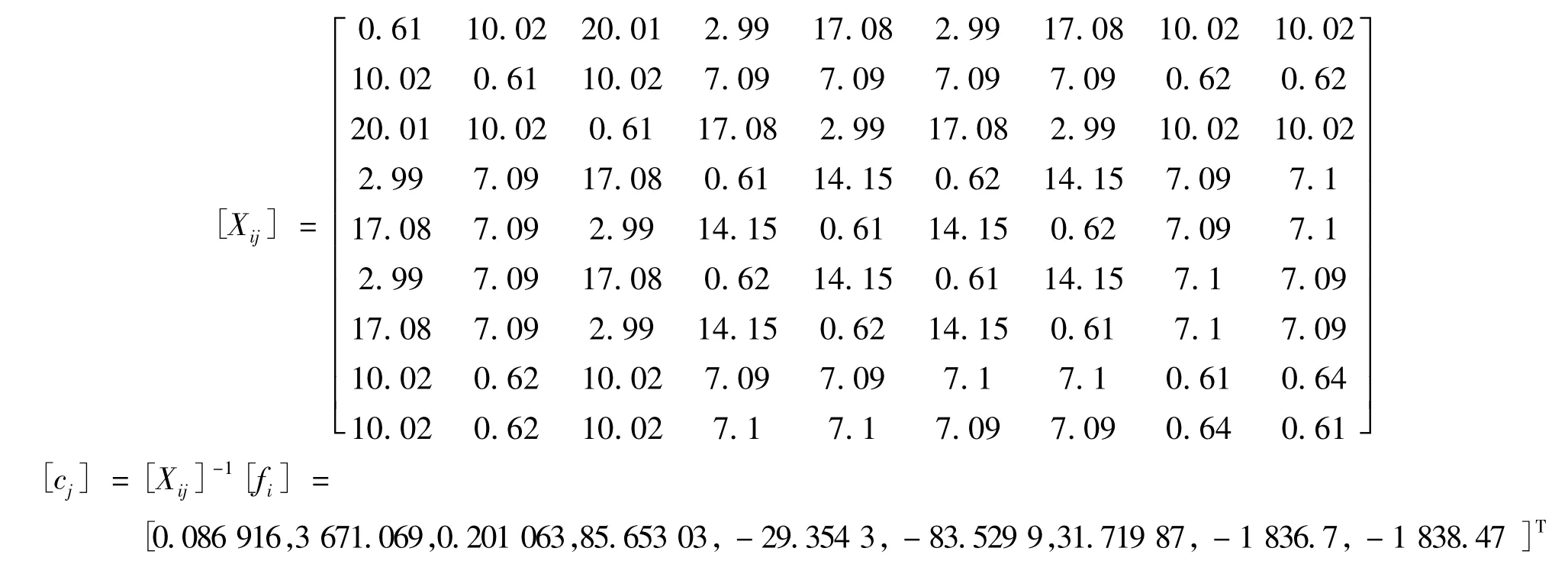
因此初始響應面函數可寫成:
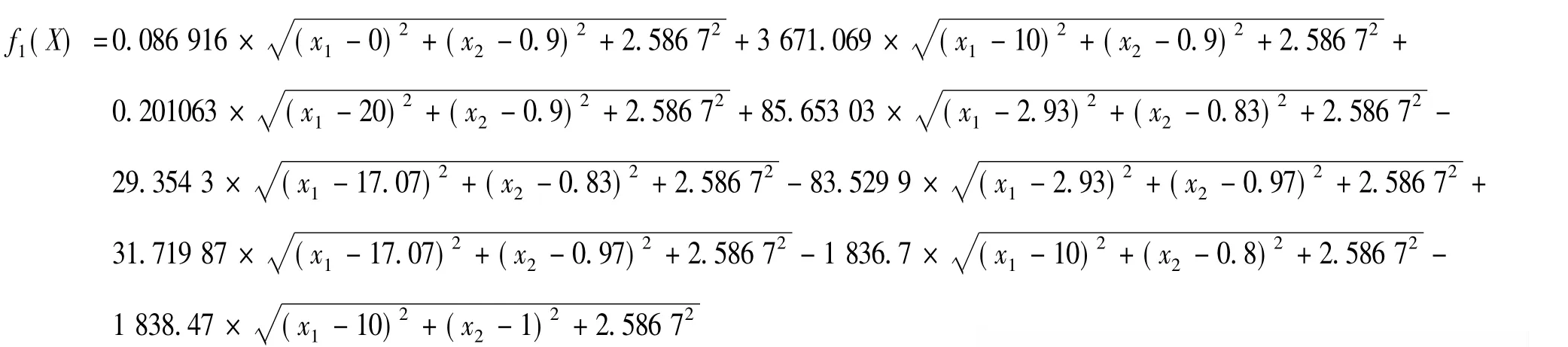
2.3響應面函數與優化結果
根據上述方法所得到的初始響應面函數如圖4所示。
對以上初始響應面函數應用遺傳算法求解其最小值點,得(17.49,1)。
將遺傳算法[9]應用于磁鋼形狀的響應面法,具體實現如下:

圖4 響應面函數
(1)參數編碼:采用浮點數編碼,在本文中個體的編碼長度為2。
(2)個體的適應度評價:在本文中選擇等差為2,最適應的個體適應度值為2,最差個體適應度值為0。
(3)遺傳操作:本文采用比例選擇。
(4)控制參數設定:本文設置群體規模為60,交叉概率為 0.7,變異概率為 0.01。
綜上,本文中遺傳算法所采取的參數如表3所示。

表3 遺傳算法所取參數
每個變量采用浮點數編碼,個體的每一個基因值用某一范圍內的一個浮點數來表示,個體的編碼長度等于變量的個數。由點(17.49,1)再次選取新的樣本點,如表4所示,表4中部分數據超出了求解區域,應當視為無效數據。

表4 優化變量與波形畸變率(新樣本點)
樣本點組的分布如圖5所示。
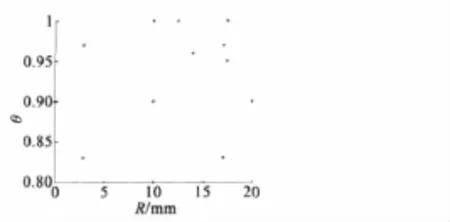
圖5 響應面函數(新樣本點)
根據上述的響應面法可得:

矩陣[Xij]的維數為13×13。
把新樣本點組中的有效點和初始樣本點組匯合在一起,重新構建響應面函數,響應面函數(新樣本點)如圖6所示。
對以上響應面函數再次通過遺傳算法求得最小值點為(17.13,1)。
當前最優點(17.13,1)與前一個最優點(17.49,1) 距離小于 0.5,故可把當前最優點(17.13,1)視為全局最優。
采用響應面法分析得到的優化前后永磁同步電動機的氣隙磁密仿真波形,如圖7所示。

圖6 響應面函數
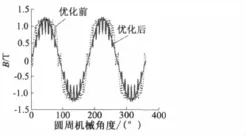
圖7 優化前后的氣隙磁密仿真波形對比
從圖中可以看出,優化后的氣隙磁密波形更加接近于正弦波。需要說明的是,仿真結果中的氣隙磁密波形的脈動是由電機定子的齒槽效應造成的,若要實現更加理想的正弦波,后續可對電機定子的齒槽進行優化。
3結 語
永磁同步電動機磁鋼的設計是解決輸出力矩脈動的關鍵。本文采用響應面法,基于磁鋼的外徑以及極弧系數進行優化設計,給出了永磁同步電動機響應面法設計的詳細過程,優化結果表明:響應面法可在較少的采樣點下求得的永磁同步電動機最佳優化磁鋼外徑和極弧系數為(17.13,1)。
[1] 冷再興,馬志源.一種新的內置式永磁同步電機弱磁調速控制方法[J].微電機,2006,39(6):11-14.
[2] 夏旎.磁懸浮飛輪用永磁無刷直流電動機參數的三維場計算方法[J].微電機,2006,39(1):9-12.
[3] 沈建新.氣隙磁場波形及磁瓦充磁方式對無刷直流電動機性能的影響[J].微特電機,2006(6):7-9.
[4] 楊云帆,李光軍,王惠軍,等.慣性動量輪電機磁極結構對轉矩脈動的影響[J].微電機,2011,44(7):6-10.
[5] 陳立周.工程穩健設計的發展現狀與趨勢[J].中國機械工程,1997,9(6):59-62.
[6] 王永菲,王成國.響應面法的理論與應用[J].中央民族大學學報 (自然科學版),2005,14(3):236-240.
[7] 文澤軍,劉德順.基于響應面模型的永磁直流微電機堵轉力矩穩健設計[J].機械設計與制造,2007(3):16-18.
[8] 王雅玲,徐衍亮,劉西全.雙定子永磁同步發電機(I)-結構原理及其響應面法設計[J].電工技術學報,2011,26(7):167-172.
[9] 周明,孫樹棟.遺傳算法的原理與應用[M].北京:國防工業出版社,2001.

