減小永磁直線電動機齒槽力的分析研究

黃文美，楊 帥

(河北工業大學，天津300130)

0引 言

隨著新的磁性材料的發現和磁性材料制作工藝的改善，永磁材料的性能得到不斷提高。永磁電機受到重視，被廣泛地應用于高精度的控制系統中。永磁直線電動機(以下簡稱PMLM)不僅具有永磁電機結構簡單、電磁污染小等特點，同時還具有直線電動機推力大、功率密度大等優點，具有較好的發展前景，其優勢在軍事、工業、民用等各種直線運動的應用場合表現得更為明顯。在往復直線運動系統中，將永磁直線電動機替代了旋轉電機作為系統的驅動裝置，取消了中間多級傳動機構，減少了系統損耗，提高了系統的效率。但是，由于PMLM的電樞鐵心兩端斷開以及齒槽的存在，使得PMLM的電磁推力產生波動，進而產生振動和噪聲，嚴重影響了PMLM的控制性能。因此，減小永磁直線電動機的推力波動是分析和研究永磁直線電動機重要內容之一。

PMLM的推力波動主要由直線電動機的端部效應力和齒槽效應力造成的。端部效應力的削弱可以通過修正鐵心末端部分的形狀［1］，或者采取改變電樞鐵心長度的方法來實現［2］。而齒槽力的削弱，文獻［3］提出采用分數槽減小齒槽力，但沒有進一步分析它們之間的變化規律，文獻［4］提出通過改變磁極寬度來削弱齒槽力，但只是齒槽力的二次諧波被削弱。文獻［5］從控制角度對齒槽力進行補償，這樣勢必增加電機的成本。

本文從電機設計的角度出發，根據齒槽力的解析表達式，采用改變極弧系數的方法達到削弱齒槽力的目的，并通過仿真實驗對優化方案進行驗證。

1 PMLM的推力波動分析

為了提高PMLM的推力密度，PMLM的電樞鐵心都開有齒槽用來嵌放繞線，所以PMLM存在和旋轉電機一樣的齒槽力。與具有閉合圓環形狀鐵心的旋轉電機不同的是，PMLM的鐵心是長直的，兩端不是閉合的。斷開的鐵心使得鐵心端部磁場發生了明顯變化，從而產生了其值隨著動子位置的不同而變化的端部作用力。端部作用力與齒槽力在PMLM里的示意圖如圖1所示。圖中，FA、FB為端部作用力;Fti為齒槽力。通常，在分析PMLM的推力波動時，常把由于電機鐵心開槽和兩端斷開引起的推力波動合稱為磁阻力，因為產生齒槽力和端部力的根本原因是鐵心和永磁體之間的氣隙磁阻發生了變化。

直線電動機齒槽力產生的機理和旋轉電機一樣，在電樞繞組不通電的情況下永磁體和鐵心齒槽相互作用產生的力矩。它使PMLM的動子有一種沿著某一特定方向與定子對齊的趨勢，由此趨勢會隨著直線電動機的推力一起輸出，使推力產生波動。本質上齒槽力是由齒槽結構使永磁體和鐵心之間的氣隙磁阻發生變化引起的。為了提高直線電動機的推力密度，直線電動機的齒槽必須存在，所以齒槽力只能被削弱，不能完全消除。

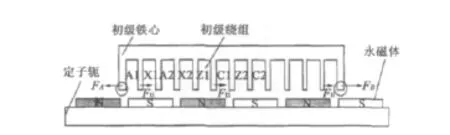
圖1 PMLM磁阻力示意圖

2齒槽力的解析分析

齒槽轉矩是電機在不通電的情況下，永磁體和齒槽間相互作用的結果。其數學表達式:

由文獻［8］可知:

式中:μ0為真空磁導率;B為氣隙磁感應強度;V為氣隙體積。

假設永磁體磁導率與空氣磁導率相同，那么，氣隙磁感應強度的近似表達式可表示:

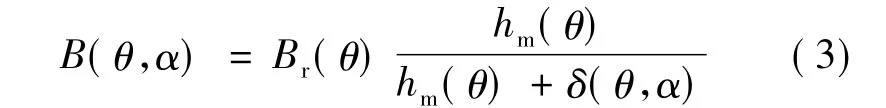
式中:Br(θ)為永磁體剩磁沿圓周方向的分布;δ(θ，α)為有效氣隙長度沿圓周方向的分布;hm(θ)為永磁體充磁方向長度沿圓周方向的分布。

將式(3)代入式(2)得:

式中:z為電樞槽數。

對于PMLM，忽略邊端效應，則直線電動機動子相對于定子沿直線方向移動的位移x，可表示為旋轉電機中偏轉的角度，即:

式中:C為直線電動機定子長度。

根據旋轉電機齒槽轉矩的定義，直線電動機的齒槽力:

將式(4)～式(7)代入式(8)得:

至此，得到了PMLM齒槽力的解析表達式。

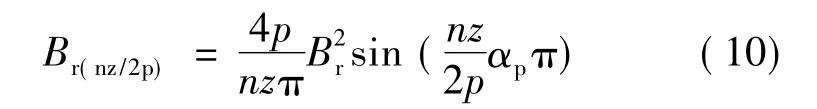
式中:m為槽極數的最大公約數。

3有限元分析

有限元法是分析磁場力較為常用的方法，本文采用有限元軟件對PMLM進行仿真實驗，從而驗證通過選取合理的極弧系數對PMLM齒槽力的削弱情況。為了較真實地反映極弧系數對齒槽力的影響，本文所建的直線電動機仿真模型的動定子材料、永磁體材料、每個齒槽結構和氣隙高度均保持不變。

本文以4極24槽和4極21槽的PMLM為仿真實驗模型。PMLM的主要參數如表1所示。

表1 電機模型參數

圖2為每極每相槽數為整數時，PMLM齒槽力隨極弧系數改變而變化的仿真圖。從圖2可以看出，優化后的極弧系數(αp=5/6)與優化前的(αp=7/9，αp=9/10)相比，齒槽力得到明顯的改善。優化前齒槽力的峰值分別為71．82 N、62．26 N，優化后齒槽力的峰值減小到42．67 N。由此，驗證了本文方法確定的極弧系數可以削弱PMLM齒槽力。

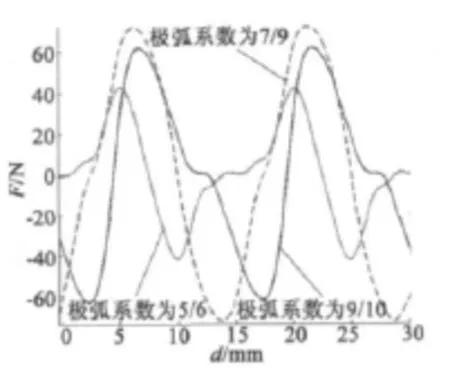
圖2 不同極弧系數時齒槽力

由式(11)確定的極弧系數不止一個，本文借助有限元軟件進一步分析了這些由式(11)確定的極弧系數與齒槽力的變化規律，如圖3所示。可以看出，隨著優化極弧系數的增大，齒槽力有減小的趨勢，但當極弧系數為1時，齒槽力反而增大很多。

圖3 不同優化極弧系數時齒槽力

以上是在每極每相槽數為整數情況下，齒槽力與極弧系數的變化關系。下面對槽極數互質時，齒槽力與極弧系數的變化規律進行有限元分析，仿真結果如圖4所示。

由圖4可知，當直線電動機的齒槽數互質時，齒槽力的變化情況不像整數槽那樣，而是隨著極弧系數的增大呈現波動情況。但使齒槽力最小的極弧系數仍然在式(11)確定的值的附近。例如當極弧系數αp=12/21≈0．57時，齒槽力最小，約為3．8 N。從而說明本文確定極弧系數的方法對槽極數互質的情況也有一定的參考價值。

圖4 齒槽力隨極弧系數的變化(4極21齒槽)

由圖5可知，當直線電動機的齒槽數互質時，改變極弧系數不僅能影響齒槽力的大小，還能對齒槽力的周期數造成影響。當齒槽力的周期數減小時，此時的齒槽力就變大。

圖5 槽極數互質時不同極弧系數齒槽力對比

由圖6可以看出，在不改變其他電機參數的情況下，采用槽極數互質的配合方法來削弱齒槽力比通過改變極弧系數的方法效果明顯好得多。對于4極24槽的直線電動機來說，優化后的極弧系數為αp=5/6，此時齒槽力的幅值約為40 N，而采用槽極數互質(4極21槽)時，齒槽力大大減小到6 N左右。

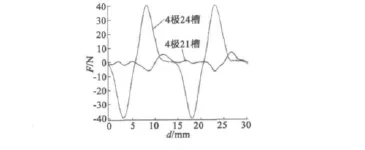
圖6 優化極弧系數和槽極數互質對齒槽力削弱的比較

4結 論

本文通過分析PMLM齒槽力的解析表達式，獲得了通過極弧系數的選擇削弱齒槽力的方法。并且運用有限元軟件對其進行仿真實驗，驗證了上述方法的正確性。在此基礎上，分析了不同槽極數情況下，齒槽力與極弧系數的變化關系，對削弱齒槽力具有一定的指導意義。

(1)當每極每相槽數為整數時，式(11)確定的極弧系數使齒槽力得到改善，并隨著極弧系數的增大，齒槽力有減弱的趨勢。考慮到磁鐵的邊端效應等因素的影響，實際的極弧系數可能要比式(11)確定的值要大些。

(2)當齒槽數互質時，齒槽力隨著極弧系數的增大呈現出波動情況。但使齒槽力最小的極弧系數仍然在式(11)確定的值的附近。從而說明本文確定極弧系數的方法對槽極數互質的情況也有一定的參考價值。另外，改變極弧系數不僅能影響齒槽力的大小，還能對齒槽力的周期數產生影響。當齒槽力的周期數減小時，此時的齒槽力就變大。

(3)通過比較極弧系數與槽極數配合對齒槽力的削弱情況，發現采用槽極數互質比采用優化的極弧系數對齒槽力削弱的程度要大。

［1］ 吳昊，張之敬，劉成穎．永磁直線電機縱向端部效應補償方法［J］．中國電機工程學報，2010，30(36):46-52．

［2］ Inoue M，Sato K．An approach to a suitable stator length for minimizing the detent force of permanent magnet linear synchronous motors［J］．IEEE Transactions on Magnetics，2000，44(36):1890-1893．

［3］ 鄭光遠，肖曙紅，陳署泉．永磁同步直線電機分數槽繞組諧波分析和齒槽力研究［J］．機械與電子，2009(8):65-67．

［4］ 羅宏浩，吳峻，常文森．動磁式永磁無刷直流直線電機的齒槽力最小化［J］．中國電機工程學報，2007，27(6):12-16．

［5］ 陸華才，江明，郭興眾，等．永磁直線同步電機推力波動約束［J］．電工技術學報，2012，27(3):128-132．

［6］ Chen Yaow-ming，Fan Shu-yuan，Lu Wei-shin．Performance analysis of linear permanent-magnet motors with finite-element analysis［J］．IEEE Transactions on Magnetics，2008，44(3):377-385．

［7］ 潘開林，傅建中，陳子辰．永磁直線同步電機的磁阻力分析及其最小化研究［J］．中國電機工程學報，2004，24(4):112-115．

［8］ 王秀和．永磁電機［M］．北京:中國電力出版社，2007．

［9］ 王秀和，楊玉波，丁婷婷，等．基于極弧系數選擇的實心轉子永磁同步電動機齒槽轉矩削弱方法研究［J］．中國電機工程學報，2005，25(15):146-149．

［10］ Selcuk A H，Kurum H．Investigation of end effects in linear induction motors by using the finite-element method ［J］．IEEE Trans．on Magnetics，2008，44(7):1791-1795．

［11］ Isfahani A H，Ebrahimi B M，Lesani H．Design optimization of a low-speed single-sided linear induction motor for improved efficiency and power factor［J］ IEEE Trans．on Magnetics，2008，44(2):266-272．

［12］ Tomczuk B，Schroder G，Waindok A．Finite-element analysis of the magnetic field and electromechanical parameters calculation for a slotted permanent-magnet tubular linear motor［J］．IEEE Transactions on Magnetics，2007，43(7):3229-3236．