軸向永磁軸承的設計與試驗驗證

張鋼，孫昌，張堅，張海龍，蔣德得

(上海大學 機電工程與自動化學院軸承研究所，上海 200072)

主動磁懸浮軸承是利用可控磁場力提供無接觸支承，使轉子穩定懸浮于空間且其動力學性能可由控制系統調節的一種新型高性能軸承，其研究涉及機械學、電磁學、電子學、轉子動力學、控制理論和計算機科學。它是一種典型的機電一體化產品[1]，但造價過于昂貴，且需要專業技術水平很高的人員進行安裝維護，因此在國內尚未能得到廣泛應用。

永磁懸浮軸承(簡稱永磁軸承)是利用永磁體產生的磁場力將轉子懸浮起來，不需要主動電子控制系統，減少了復雜電子控制器件可能失效的風險，系統也將更加可靠，使用壽命更長。永磁軸承作為被動磁懸浮軸承的一種[2]，目前雖然已在電表、風力發電機和永磁懸浮列車等特殊場合得到了某些應用，但它也是與機械支承相結合的。缺點是裝配困難，需要資深專業技術人員安裝維護，還不能普遍地應用到一般的工業機械中。因此，目前國內、外還沒有像滾動軸承那樣由專業廠家生產制造的標準化和系列化的永磁懸浮軸承。

由Earnshaw定律可知，永磁軸承不能實現所有自由度的穩定[3]。因此，在永磁懸浮系統中，至少在一個自由度上需要引入其他主動支承方式。本例基于軸向永磁懸浮技術方案提出了工業應用型軸向推力永磁軸承的設計思路。文中所述的工業應用型永磁軸承是指：將永磁懸浮軸承做得像滾動軸承那樣便于安裝和使用；并能在工廠中實現標準化、系列化生產；用戶工程技術人員能像滾動軸承那樣把它設計應用到主機產品中；其制造成本與滾動軸承相當，并能夠像滾動軸承那樣得到廣泛應用[4]。

1 結構設計

軸向永磁軸承由軸向并行放置的永磁環構成，利用永磁體之間的作用力來實現懸浮物體在部分自由度上面的穩定懸浮，它不需要控制系統，懸浮功耗相對較小。文獻[5]曾提出了在一定假設基礎上建立適用于軸向磁化和徑向磁化的磁環來設計磁軸承的通用模型。由于軸向磁化磁環在加工技術工藝上容易實現，本設計系基于軸向磁化的永磁環[6]。圖1所示為軸向推力永磁軸承單元結構圖。通過調整永磁環的軸向相對位置，可獲得所需的軸向力。圖中永磁環放置的相對位置可以獲得最大的軸向力。

圖1 軸向推力永磁單元結構圖

在實際設計中，為了適應不同的工況，永磁軸承在結構上有很多選擇，可以通過采用多對磁環疊加的方法來增加永磁軸承的剛度和承載力。圖2是軸向永磁軸承結構示意圖。它由軸圈、座圈、靜永磁環、動永磁環、隔圈和保持軸承組成。永磁環材料選用N35型稀土釹鐵硼，其參數為：Hc=1 038 kA/m，Br=1.191 T。

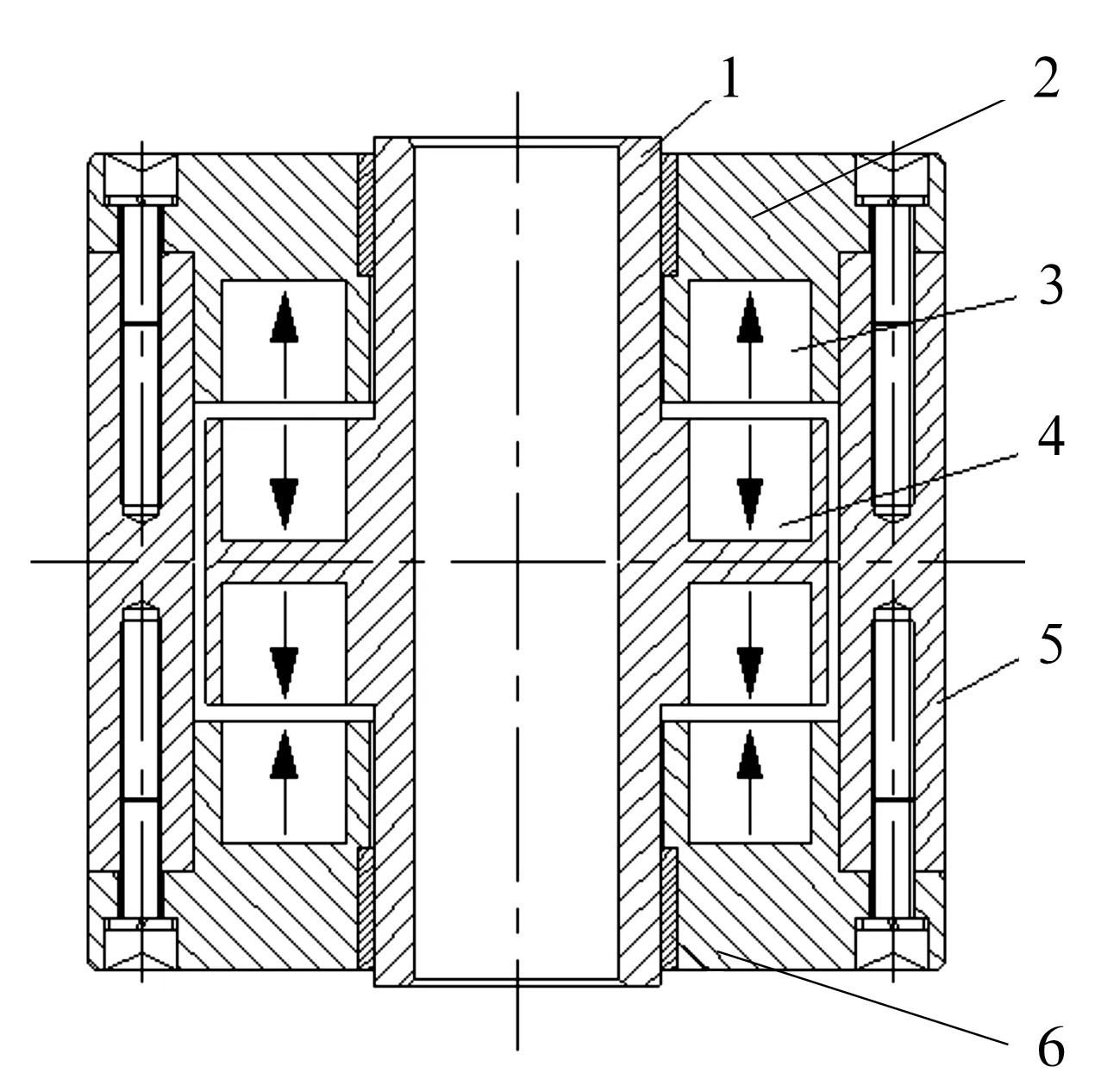
1—軸圈；2—座圈；3—靜永磁環；4—動永磁環；5—隔圈；6—保持軸承

軸向推力永磁軸承的工作原理：上、下兩座圈上的永磁環為靜永磁環，軸圈上的永磁環為動永磁環；靜永磁環磁極方向一致且與相鄰動永磁環磁極方向相反。動/靜永磁環之間的磁斥力使動磁環在受載時產生一個相反方向的恢復力，實現穩定懸浮。建立rz二維坐標系，如圖3所示：r軸表示徑向，z軸表示軸向。由于2個動永磁環之間為吸引力關系，所以可將2個動永磁環視為整體進行原理簡化分析。當動永磁環在外載荷Fz的作用下向下移動z時，下間隙減小為c-z(c為平均間隙)，上間隙增加為c+z，使得下靜永磁環對動永磁環向上的斥力Fz1大于上靜永磁環對動永磁環向下的斥力Fz2，產生一個向上的恢復力Fz1-Fz2來承受外載荷Fz，實現穩定懸浮。

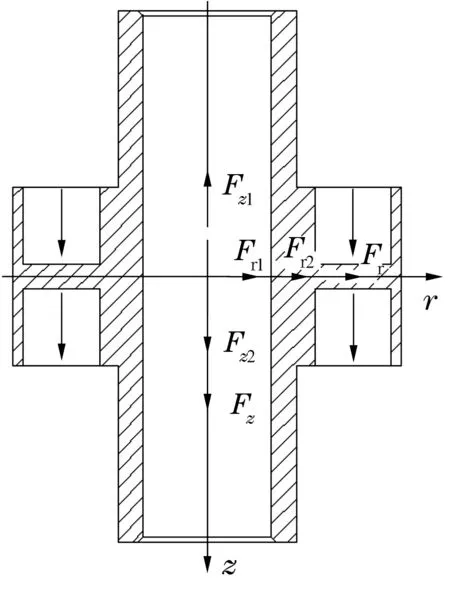
圖3 動永磁環受力圖

根據Newton第三定律，軸向外載荷Fz為

北京市召開節約用水大會。3月25日，2010年北京市節約用水大會在北京會議中心召開。會議總結了2009年北京市節水工作，部署了2010年工作任務，表彰了2009年度北京市節約用水先進單位、2009年度北京市節水系統先進集體和先進個人，并向全市中小學生代表發放了《北京之水》知識讀本，并由北京市水務局與石景山、大興等區縣代表簽署了節水目標責任書。

Fz=Fz1-Fz2，

(1)

保持軸承所受的作用力Fr為

Fr=Fr1+Fr2。

(2)

如果設計、加工和裝配良好，保持軸承的徑向間隙很小，動永磁環的徑向位移也很小，保持軸承所受的力Fr就很小，它的摩擦阻力(矩)也非常小。

軸向剛度為

(3)

徑向剛度為

(4)

2 磁力特性

為了求得軸向永磁軸承動磁環上的總磁力，需要對動磁環周圍空氣層的磁力進行求和。在有限元軟件ANSYS中，用虛功方法計算磁力可以通過能量對可移動部件位移的微分得到，空氣層單元軸線方向上磁力的基本表達式為

(5)

(6)

文獻[3]研究了采用ANSYS分析軸向軸承軸向剛度的可行性。研究結果表明，在計算永磁軸承的承載能力時有限元法數值解與試驗結果較吻合[7-10]。

本例采用ANSYS12.0軟件，完成了軸向永磁軸承的承載能力分析。借助于ANSYS中關于電磁場的分析方法，選用SOLID98單元類型進行磁環完整建模，建模后進行網格劃分，并給其施加Maxwell面標志和虛功位移邊界條件，求解后可以得到動永磁環在組合磁場中的軸向力數值。對動/靜永磁環間隙(軸向間隙)c分別為2，6，11和21 mm時的軸向力進行計算，并根據計算結果數據繪制動永磁環軸向力與軸向位移的關系曲線如圖4所示。

圖4 永磁軸承軸向力與軸向位移擬合曲線

從圖4可以看出，軸向間隙越小，相同位移下的承載力就越大，軸向剛度也就越大。因此可以得出：c=2 mm時Kz≈169.02 N/mm；c=6 mm時Kz≈83.096 N/mm；c=11 mm時Kz≈39.480 N/mm；c=21 mm時Kz≈11.710 N/mm。理論軸向剛度為正則說明軸向可以穩定承載。

下面以軸向間隙2 mm為例，對動靜永磁環進行ANSYS建模，研究動永磁環在一定范圍的偏心距內變化時徑向力所呈現的特性。具體數值見表1，對徑向位移0 ～0.20 mm之間的數據進行曲線擬合(圖5)。

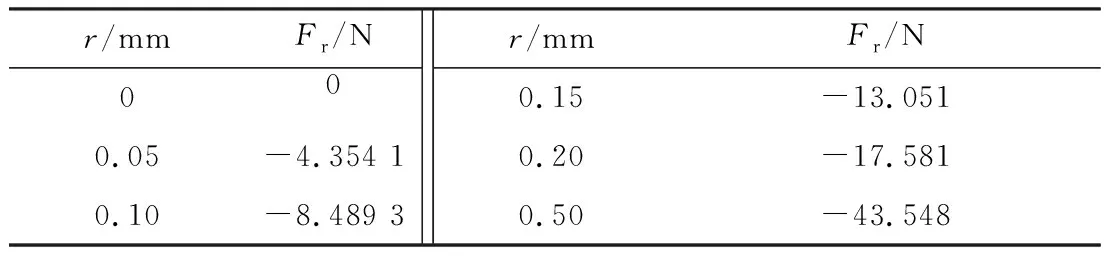
表1 徑向力隨徑向偏心距變化關系(c=2 mm)

圖5 徑向力隨徑向偏心距變化的擬合曲線

由圖5可知，在較小的偏心距范圍內，動永磁環在徑向上受到靜永磁環對它的徑向斥力，而且斥力大小隨著偏心距的增大而增大。動永磁環在徑向上不會受到向軸線拉近的回復力，因此動永磁環不具有自動對心能力。

由圖5可知：當c=2 mm時，徑向剛度Kr≈-86.796 N/mm，徑向剛度為負說明徑向不穩定，必須加徑向滑動保持軸承。

表1中當徑向偏移量為0.5 mm時所對應的徑向力約45 N，數值偏大，故實際設計中徑向偏移量不宜過大，一般控制在0.05 mm以內，此時所對應的徑向力約為4 N，降低了對徑向保持軸承的壓力，摩擦阻力非常小。

3 試驗驗證

為了測量軸向永磁軸承在軸向較大范圍內的承載力Fz，選擇摩擦因數非常小的滑動軸承作為保持軸承。

試驗中對軸向永磁軸承施加軸向載荷，以測量其承載力和剛度。將軸向推力永磁軸承軸向放置，放上標稱測量砝碼。為了測得準確的數據，加工了與隔圈內、外徑相等，厚度分別為2，3，5和10 mm規格的調整圈。調整圈分別安裝在隔圈與座圈接觸表面(圖6)，以調整試驗中最關鍵的磁環間隙。試驗測量原理示意圖如圖7所示。

1—軸圈；2—座圈；3—靜永磁環；4—動永磁環；5—隔圈；6—保持軸承c7—調整圈

圖7 試驗測量原理示意圖

理論上可以測得磁環間隙從1～21 mm超過40組以上的數據。本例只測量了幾組有代表性的間隙，分別為1，2，6，11和21 mm。值得注意的是，選擇間隙為1 mm試驗時，當承載力增加到一定數值時就會出現磁環觸碰現象，所以出于安全性考慮不予選擇。表2和表3分別列出動/靜磁環之間的最大間隙21 mm以及最佳間隙2 mm時的測量數據。

表2 間隙21 mm時軸向永磁軸承試驗數據

表3 間隙2 mm時軸向永磁軸承試驗數據

由兩組數據不難看出載荷與相對下垂位移之間的關系，由此便可得出軸承承載力與軸向位移(相對下垂位移)之間的關系。

調整永磁環間隙，最后得到如圖8所示的力學特性試驗曲線。

圖8 軸向永磁軸承承載力與軸向位移曲線

對不同間隙下軸向永磁懸浮軸承軸向載荷與軸向位移試驗值進行曲線擬合，由圖8可以驗證理論計算得出的結論，即軸向氣隙越小，相同位移下的承載力就越大，軸向剛度也就越大。試驗得到的軸承剛度為：c=2 mm時，Kz≈174.5 N/mm；c=6 mm時，Kz≈84.9 N/mm；c=11 mm時，Kz≈42 N/mm；c=21 mm時Kz≈15.5 N/mm。在軸向承載能力上，試驗值與理論值最大偏差為3.24%。

4 結束語

所設計的軸向推力永磁軸承采用工業化應用理念進行設計，其結構簡單可靠、減少了目前永磁軸承散件自行組裝帶來的不便，具有使用方便、摩擦力小、節能以及適應于大規模應用等優點。

試驗驗證結果表明：軸向永磁軸承的軸向承載力隨軸向位移的增大而增大；軸向間隙越小，軸向剛度就越大；小范圍的徑向偏移，對軸向載荷影響不大。