回歸分析和BP神經網絡在地表沉降監測中的應用①

陳 帥，朱小玉，王 鵬，姜 楠

（安徽理工大學 測繪學院，安徽 淮南232001）

0 引 言

在地表沉降監測中，準確地對監測點的變形進行預測是非常必要的，隨著計算機應用水平的快速提高，現階段預測沉降的數學模型和方法有許多。為提高數學模型在地表沉降監測及規律預測中的準確性，采用了回歸分析法中的曲線擬合法和BP神經網絡模型的數值處理方法并進行比較，得到模型適合預測的范圍。

1 模型的基本原理

1.1 回歸分析法

回歸分析法是利用數理統計原理，對大量的統計數據進行數學處理，并確定因變量與自變量之間的相關關系，建立一個相關性較好的回歸方程，并加以外推，用于預測因變量的分析方法，是最常用的數理統計方法。通常線性回歸分析法是最基本的分析方法，而求一個變量對另一個變量的因果關系，叫一元回歸分析。

設以x為自變量，y為因變量，則一元線性回歸模型可表示為

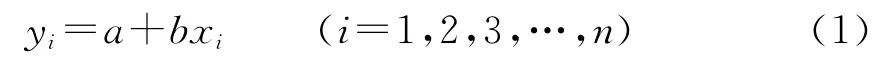
式中：a、b為回歸系數；i為觀測次數。

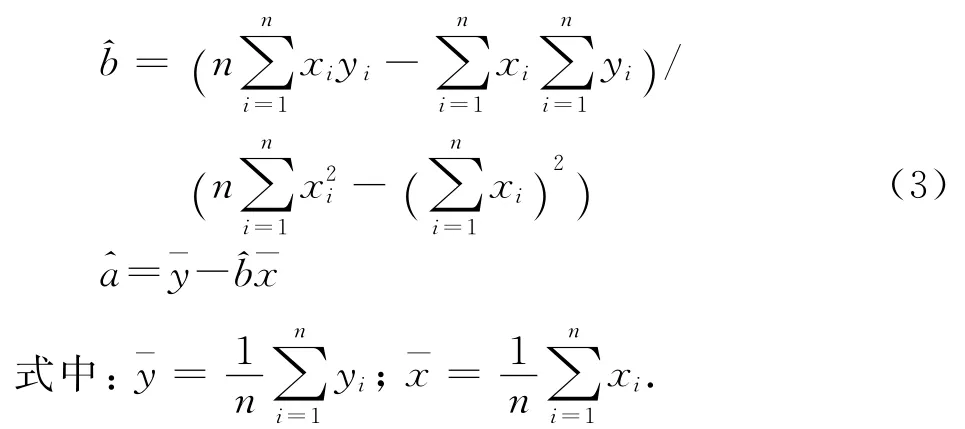
1.2 BP神經網絡模型

BP神經網絡是一種基于誤差反向傳播算法的多層前饋網［2]。它是一種由輸入層、隱含層和輸出層構成的多層向前神經網絡，本質是以網絡誤差之平方和為目標函數，按梯度法求其目標函數達到最小值的算法。其主要特點是：每個激勵函數是可微的Sigmoid函數；多層感知器的多個突觸使得網絡更具連通性，連接域的變化或連接權值的變化都會引起連通性的變化［3]。圖1為BP神經網絡的拓撲結構。

BP算法的學習過程就是使能量函數最小化的過程，由兩部分組成：信息的正向傳遞與誤差的反向傳播。在正向傳播過程中，輸入信息從輸入層經隱含層逐層計算傳向輸出層，每一層神經元的狀態只影響下一層神經元的狀態。如果在輸出層未得到期望的輸出，則計算輸出層的誤差變化值，然后轉向反向傳播，通過網絡將誤差信號沿原來的連接通路反傳回來修改各層神經元的權值直至達到期望目標［3]。

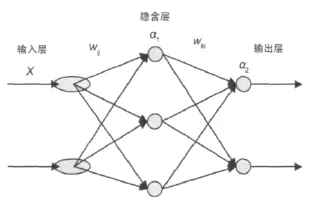
圖1 BP神經網絡的拓撲結構

假設輸入為x，輸入神經元有r個，隱含層內有s1個神經元，激活函數為f1，輸出層內有s2個神經元，對應的激活函數為f2，輸出為a，目標失量為t，則隱含層中第i個神經元的輸出為

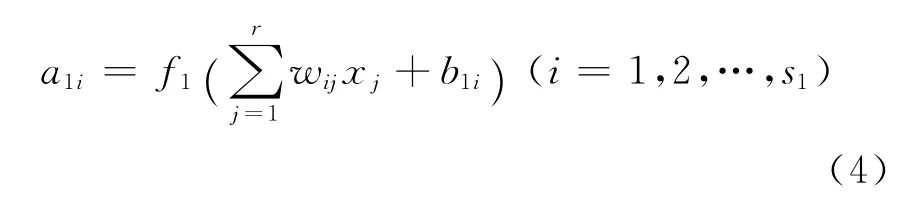
輸出層第k個神經元的輸出為

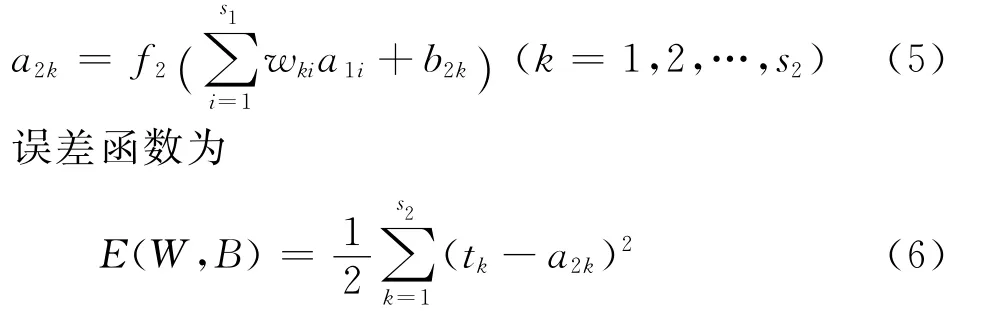
輸出層的權值變化為

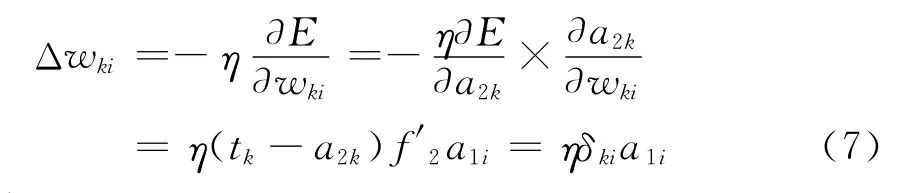
式中：δki＝（tk－a2k）f′2＝ekf′2；ek＝tk－a2k.同理可知

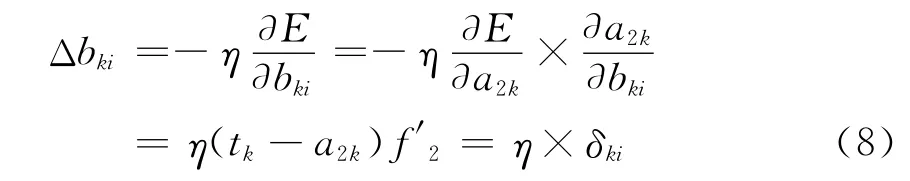
隱含層權值變化為

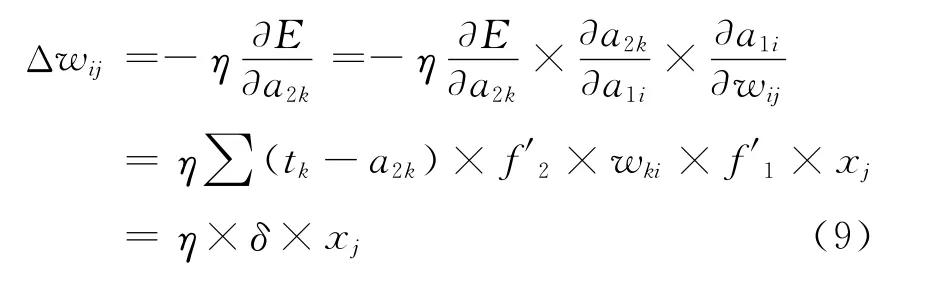
同理可得

Δb1i＝ηδij

對于f1為對數S型激活函數

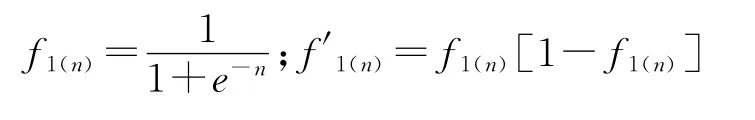
對于f2線性激活函數

f′2（n）＝n′＝1

為加快訓練速度，避免陷入局部極小值，可采用附加動量法、變尺度法和變步長法進行BP網絡的改進。這里用的是附加動量法。

帶有附加動量因子的權值調節公式［5]

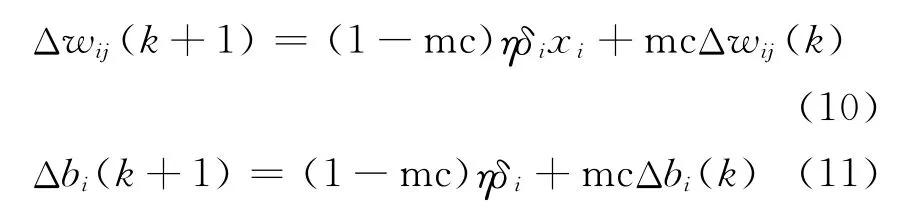
式中：k為訓練次數；mc為動量因子，一般取0.95.

2 模型對比

采用某礦區的實測資料，通過建立兩種預測模型的數學源程序模型，輸入原始數據資料，分別用以上兩種模型進行預測訓練和測試，得到預測模型，輸入預測時間，即可得到具有相當精度的預測量，如表1所示。

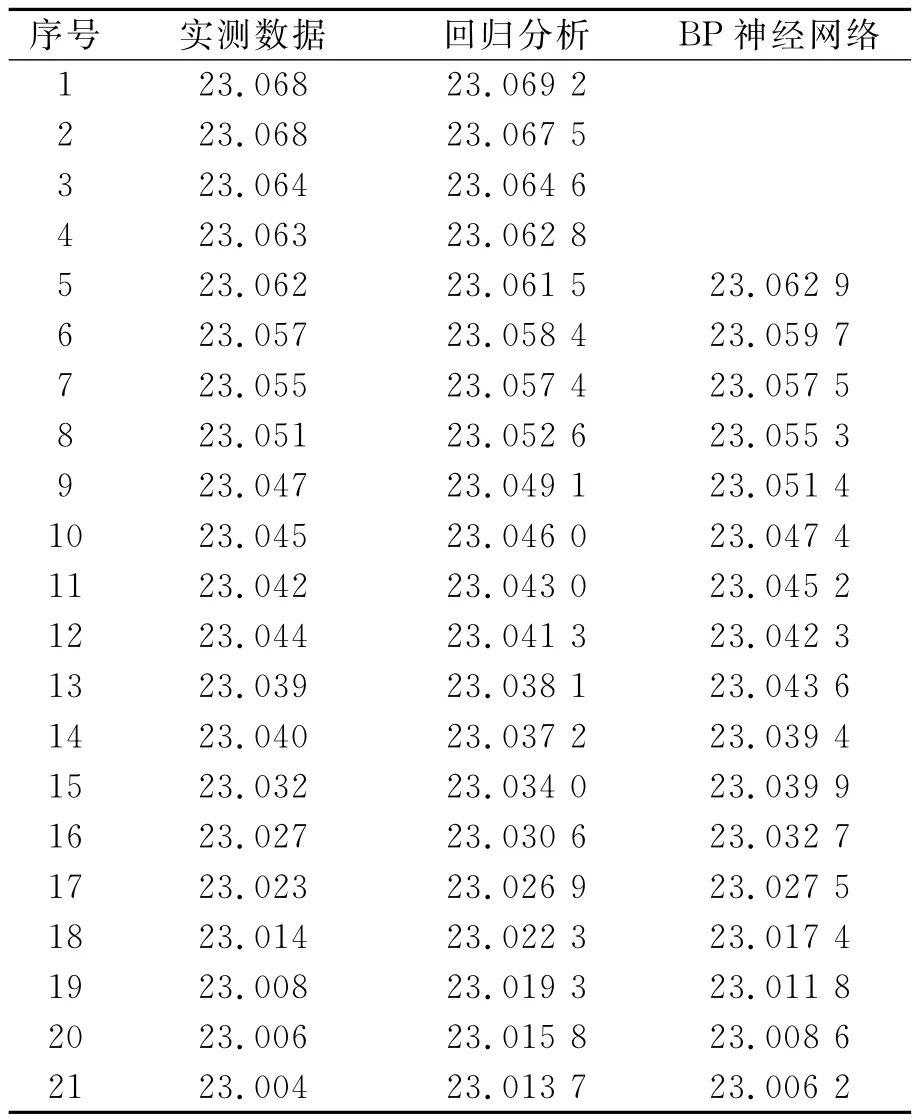
表1 模型在實測點預測結果相比較／m

通過兩種預測模型的預測值與實測值比較可以看出，在前期的預測中，采用回歸分析和BP神經網絡預測的結果和實測值擬合的比較好。后期由于數據的跳躍性，采用BP神經網絡預測的結果比回歸分析法預測的結果要好，如圖2所示。

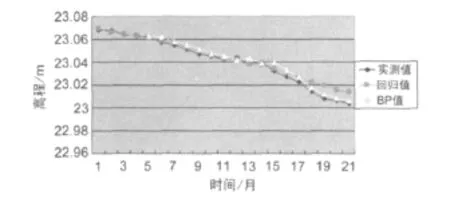
圖2 模型預測值比較

3 結 論

通過樣本訓練和測試，得到了回歸分析法中的曲線擬合法和BP神經網絡模型在地表沉降預測中各自的有效性和精確性。地表沉降預測是一種快速準確預計地表下沉的方法，選擇合適的預測模型進行預測，對提高信息預測的精度和準確度有著積極的意義。

［1]孫 華.一元線性回歸模型設計及C＋＋實現［J].長沙醫學院學報.2008（12）：47.

［2]MARTIN T H，HOWARD B D，MARK H B.神經網絡設計［M].戴 蔡譯.北京：機械工業出版社，2002.

［3]高 雋.人工神經網絡原理及仿真實例［M].2版.北京：機械工業出版社，2007.

［4]申 哲，葛廣英，田存偉.淺析BP神經網絡設計中的關鍵問題［J].科技信息，2011（6）：238－239.

［5]劉啟中，施一萍，白彩英.基于BP神經網絡的盾構施工變形預測［J].計算機應用與軟件，2005（4）：3－5.