格網(wǎng)內插法坐標轉換①

張成校，顧和和

（中國礦業(yè)大學 環(huán)境與測繪學院，江蘇 徐州221008）

0 引 言

2008年7月，2000國家大地坐標系（CGCS2000）正式使用，基于1954北京坐標系（BJS54）和1980西安坐標系（XAS80）的各種坐標成果需要轉換到CGCS2000。我國使用的1954年北京坐標系（BJS54）和1980年西安坐標系（XAS80），由于受當時技術手段的限制，存在較大的系統(tǒng)誤差和累積誤差，控制網(wǎng)間存在著扭曲變形；而基于GPS、VLBI、SLR等空間技術標定的CGCS2000精度均勻，不存在明顯的誤差積累且控制網(wǎng)間具有較好的一致性。為使轉換后的坐標與新坐標系具有較好的一致性，同時滿足各種比例尺地形圖特別是大比例尺地形圖的坐標轉換精度需求，需要研究高精度坐標轉換方法。日本、美國、澳大利亞［1－5]等國普遍采用格網(wǎng)法作為其大地坐標的主要的轉換模型，完成了新舊坐標系的轉換，取得了很好的轉換精度。如日本采用克里金內插法，生成30s×45s的格網(wǎng)數(shù)據(jù)，轉換精度達到±0.02 m。美國采用最小曲率內插法生成格網(wǎng)，全國分為多個區(qū)域，精度在±0.05～±0.5m.澳大利亞采用最小二乘配置內插格網(wǎng)節(jié)點改正數(shù)，全國分為多個區(qū)域，AGD84與GAD94之間轉換精度達到±0.04～±0.05m，AGD66與 GAD94之間轉換精度達到±0.03～±0.23m.

1 格網(wǎng)內插法原理

格網(wǎng)內插法坐標轉換的基本思想［4－8]是將大的轉換區(qū)域劃分成小的格網(wǎng)單元，利用兩個系統(tǒng)間離散點的坐標差，采用一定的內插方法計算具有一定間隔的格網(wǎng)節(jié)點的坐標差，利用格網(wǎng)節(jié)點上的坐標差內插其它任意點上的坐標差，實現(xiàn)不同坐標系坐標的變換。格網(wǎng)內插法原理如圖1.

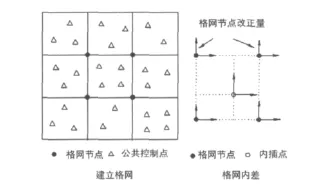
圖1 格網(wǎng)內插法原理圖

1.1 建立格網(wǎng)

將轉換區(qū)域劃分為具有一定間隔的規(guī)則格網(wǎng)，利用該區(qū)域內的若干個具有新舊兩套坐標的公共點的坐標差值，使用數(shù)學模型求得各個規(guī)則格網(wǎng)節(jié)點對應的轉換到新坐標系的改正量。

1.2 格網(wǎng)內插

根據(jù)待求點所處的格網(wǎng)單元，提取格網(wǎng)文件對應的4個格網(wǎng)節(jié)點的坐標改正量，采用雙線性內插模型進行插值計算。原理如圖2所示。

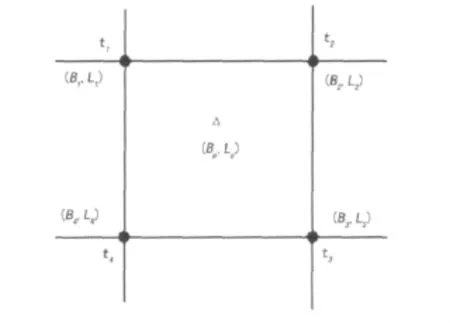
圖2 由格網(wǎng)節(jié)點內插某一點的坐標改正量

雙線性內插的公式為

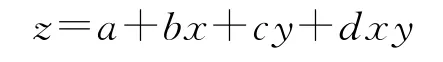
其中：

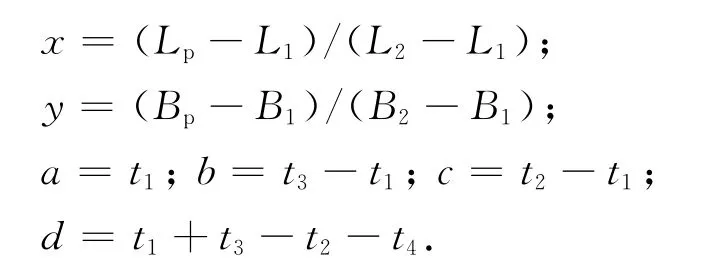
t1，t2，t3，t4分別為內插點（三角形表示）周圍的4個格網(wǎng)節(jié)點的坐標改正量；（B1，L1）、（B2，L2）、（B3，L3）、（B4，L4）分別為4個格網(wǎng)節(jié)點所在舊坐標系的經(jīng)緯度坐標；（Bp，Lp）為待求點的經(jīng)緯度坐標；z為待求點的坐標改正量。

1.3 計算步驟

1）按照一定的經(jīng)緯度間隔，轉換區(qū)域被劃分成規(guī)則的格網(wǎng)根據(jù)公共點的坐標差，用最小二乘回歸擬合一個簡單的平面模型：ax＋by＋c＝z（x，y）；

2）用平面回歸模型擬合值減去已知值得到一組殘差；

3）用數(shù)學模型將格網(wǎng)節(jié)點周圍一定搜索半徑內公共點的殘差擬合到格網(wǎng)節(jié)點上，得到格網(wǎng)節(jié)點上的殘差值；

4）格網(wǎng)節(jié)點上的平面回歸模型擬合值加殘差值，得到格網(wǎng)節(jié)點上對應的新舊坐標系坐標改正量；

5）經(jīng)雙線性內插得到格網(wǎng)區(qū)域內任意一點的坐標改正量，加到舊坐標上就得到了轉換后的新坐標，從而完成坐標轉換。

2 格網(wǎng)內插法的數(shù)學模型

求取格網(wǎng)節(jié)點改正量的數(shù)學模型可以有多種選擇，這里簡單地介紹了幾種模型。

2.1 加權平均模型

加權平均模型［6－7]根據(jù)周圍數(shù)據(jù)點對于中心點的遠近分配不同的權重，離中心點越近的數(shù)據(jù)點對中心點的影響越大，占的權重就越大，反之占的權重就越小。一般形式為

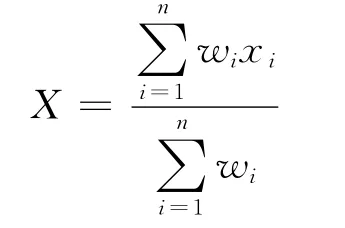
其中：X是中心點處的估值；xi是中心點周圍數(shù)據(jù)點；wi是數(shù)據(jù)點對應的權。權函數(shù)有多種形式，這里取wi＝，di是數(shù)據(jù)點到中心點的距離，dmin是各數(shù)據(jù)點到中心點的最小距離。

2.2 克里金內插模型

克里金內插法［9－10]以由區(qū)域化隨機變量z（x）的變異函數(shù)γ（x，y）或期望μ（x）＝E［z（x）]和協(xié)方差函數(shù)c（x，y）量化的隨機模型為基礎，由未觀測點x0附近x1、x2、…、xn處的觀測值zi＝z（xi）（i＝1，…，n）內插z（x）在x0處的值z（x0），得到z（x0）的最優(yōu)無偏估計量＾z（x0）。

克里金內插法的一般公式為

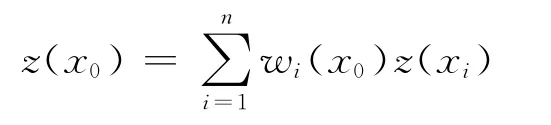
式中：z（xi）為采樣點xi處的觀測值；x0是一個未采樣點；wi（x0）為賦給觀測值z（xi）的權，其估算服從無偏條件

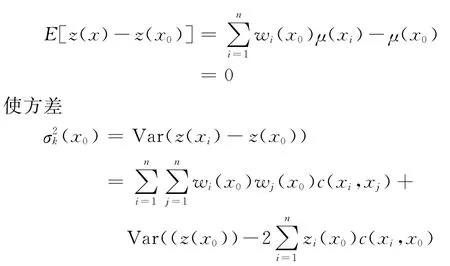
最小的條件下得到。

普通克里金法的應用條件是：區(qū)域化隨機變量滿足內蘊假設條件，即隨機變量z（x）的數(shù)學期望為常數(shù)；有足夠的觀測量確定變異函數(shù)，即隨機變量的變異函數(shù)γ（x，y）為已知。

2.3 最小曲率模型

最小曲率法［7]通過將具有觀測值的區(qū)域格網(wǎng)化，在盡可能尊重觀測值的前提下，以總曲率最小的原則生成最平滑的曲面。格網(wǎng)點（xi，yi）上的曲率為

3 算例比較

由于CGCS2000坐標數(shù)據(jù)比較少，因此，只取某地區(qū)124個具有北京54坐標和CGCS2000坐標的點進行轉換比較，其中均勻的提取其中的14個作為檢核點；為了便于格網(wǎng)的劃分，將該區(qū)域取為矩形，緯度跨度為3°，經(jīng)度跨度為4°.分別用Bursa模型和最小曲率模型進行坐標轉換，對轉換結果進行比較。

方案1：使用Bursa模型計算待求點的坐標轉換值，即計算得到的CGCS2000坐標值；將其與已知的CGCS2000坐標值進行比較得到相應的殘差，如表1所示。

方案2：利用最小二乘曲率模型構建格網(wǎng)并內插待求點得到一組殘差，如表2所示。

兩種方案轉換的結果將按殘差平均值、標準偏差、絕對值最大值這三項指標進行比較。為便于分析，經(jīng)緯度殘差均換算成弧長，以m為單位。

表1 Bursa模型的殘差統(tǒng)計

表2 最小曲率模型的殘差統(tǒng)計

從表1看出，方案1的殘差平均值和標準差較大，最大殘差絕對值接近3m，殘差的數(shù)量級基本在0.1m以上；從內部殘差統(tǒng)計來看，絕對值小于0.1m的不到10%，說明模型內符合不好；從外部殘差統(tǒng)計來看，絕對值小于0.1m的不到7%，說明模型外符合不好。這反映了我國天文大地網(wǎng)存在較大局部系統(tǒng)差。如果整個區(qū)域采用Bursa模型進行坐標轉換，將不能顧及天文大地網(wǎng)的局部扭曲和累積誤差，不能充分的擬合新舊坐標系間的坐標差異。

從表2看出，方案2轉換結果的各項指標都明顯好于方案1，從內部殘差統(tǒng)計來看，標準差降到了厘米級，殘差絕對值在0.3m以內，系統(tǒng)差已基本被消除，殘差絕對值小于0.1m所占的比例超過了93%，說明最小曲率模型內符合精度較好。從外部殘差來看，殘差平均值和標準差都比方案1大大減小，絕對值最大值控制在0.6m以內，殘差絕對值小于0.1m所占的比例超過了80%，說明最小二乘曲率模型的外符合精度也較好。總之，最小曲率模型較好地擬合了新舊坐標系間的坐標差異，有效地控制了天文大地網(wǎng)的局部扭曲和積累誤差。

4 結 論

我國CGCS2000剛剛啟用，也涉及到新舊坐標的轉換問題。相對于采用Bursa模型進行坐標轉換，采用格網(wǎng)內插轉換方法轉換精度高，適合用來實現(xiàn)高精度坐標轉換。采用格網(wǎng)內插法坐標轉換需要較多的公共點，公共點數(shù)量較多，則轉換效果較好；若公共點的數(shù)量較少，則轉換效果不明顯。

［1]施建平.美國等國家大地坐標系的更新轉換和維持［J].科協(xié)論壇，2009（7）：112－113.

［2]DEWHURST W T.NADCON－The application of minimum curvature derived surfaces in the transformation of positional data from the north american datum of 1927to the north american datum of 1983［R].NOAA Technical Memorandum NOSNGS－50，1990.

［3]MIKIO T.Coordinate transformation software“TKY2JGD”from Tokyo datum to a geocentric reference system，Japanese geodetic datum 2000［J].Times of Geographical Survey Institute，2001（97）：31－57.

［4]COLLIER P.Developmemt of Australia’s national GDA94transformation grid［R].Consultant’s Report to the Intergovernmental Committee On Surveying and Mapping，2002.

［5]李克恭，牛岸英，張斌才，等.格網(wǎng)法實現(xiàn)基礎測繪成果向CGCS2000的整體轉換［J].礦山測量，2010（4）：68－70.

［6]郭 充，呂志平，李 巖，等.基于格網(wǎng)的坐標轉換方法［J].信息工程大學學報，2010，11（2）：166－169.

［7]郭 充，呂志平，徐基剛.幾種模型在格網(wǎng)坐標轉換應用中的比較與分析［J].測繪通報，2009（5）：38－41.

［8]郭 充，呂志平，于興超，等.基于Bursa加權模型的格網(wǎng)坐標轉換［J].測繪科學技術學報，2009，26（2）：86－88.

［9]施建平，楊華忠.克里金內插法實現(xiàn)坐標轉換的應用研究［J].海洋測繪，2010，30（4）：30－32.

［10]張景雄.空間信息的尺度、不確定性與融合［M].武漢：武漢大學出版社，2008：83－129.