長度計量基礎知識講座（三十六）

/上海市計量測試技術研究院

第三十六講 測繪概況

1 測繪工作的主要內容

測繪離不開測繪儀器。作為用于國家土地規劃、工程建設、國防與地震監測等的各種測繪儀器如水準儀、經緯儀、測距儀、全站儀和GPS等是測繪過程中不可缺少的計量器具。在介紹測繪儀器之前，簡單介紹測繪工作的主要內容。

測繪學是研究和確定地面和空間的點位相對位置的科學。它的內容一是將地球上的地貌、地物、行政和權屬范圍測繪成圖或構成數字模型；二是將規劃和建筑設計的點和線在實地定位。按測繪研究和應用的重點范圍分類，可分為以下幾門主要學科：

1.1 大地測量

研究和測定地球表面廣大地區的點的定位及地球的形狀、大小和地球重力場。

1.2 地形測量

研究和采集地表局部地區的自然地貌、人工建筑及權屬界線等測繪成圖或形成數據庫。

1.3 工程測量

研究工程建設在設計、施工和管理階段中進行測量工作的理論、技術和方法。

1.4 攝影測量

研究利用攝影或遙感手段獲取地物和地貌或某構筑物的影象和光譜，進行分析和處理以確定其形狀、大小和位置，繪制成圖或提供數字文件。

2 地球的形狀和大小

人們在地球上進行建設和測量作業，必須了解地球的形狀和大小。利用測繪儀器確定地面和空間點位的坐標系。

地球自然表面極為復雜，有高山、深谷、丘陵、平原和河川、海洋等。其中海洋占整個地球表面的71%，而地球上最高的珠穆朗瑪峰8 844.43 m，最低的馬里亞納海淵在海面下11 022 m，這些高低起伏相對于地球半徑（6 371 km）來說是很小的。于是地球總的形體可設想成一個處于靜止狀態的平均海水面延伸穿過陸地所包圍的形體。海洋或湖泊在自由靜止時的表面，稱為“水準面”。水準面是受地球重力影響而形成的。受漲、落潮的影響，水準面有無數多個，其中與平均海水面相吻合的水準面稱為“大地水準面”。水準面是一個處處與鉛垂線方向垂直的曲面。由于地球內部質量分布不均勻，使鉛垂線方向引起變動，致使大地水準面成為一個略有起伏而不規則的復雜曲面。在該曲面上無法進行測量結果計算。為此，人們就選用一個非常接近大地水準面，并可用數學式表示的旋轉橢球面來代替它，表示地球總的形狀。它是一個橢圓繞其短軸旋轉而成，其旋轉軸與地球自轉軸重合，稱為“總地球橢球”，簡稱“總橢球”,見圖1。事實上，全球統一的與整個地球的大地水準面密切配合的總橢球也很難精確求定，因為在占全球2/3的大洋面上很難取得相關的精確資料。所以各國只能采用與本地區大地水準面密切配合的橢球面，作為測量計算的基準面。稱這種橢球為“參考橢球”。因此總橢球應只有一個，而參考橢球則有多個，各國不盡相同。

決定橢球體形狀和大小的元素為橢圓的長半徑a、短半徑b。并由此可算出另一個參數：偏率f；其關系式為

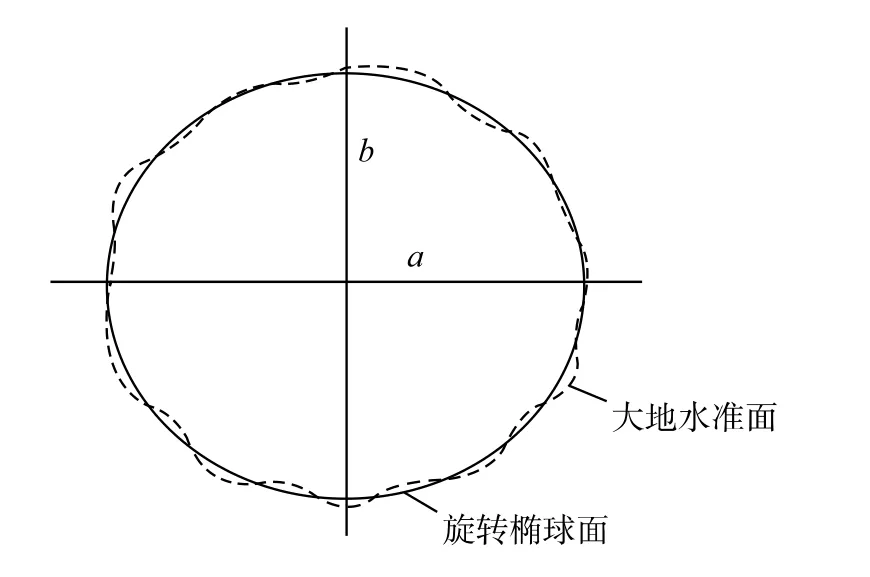
圖1 總地球橢球

我國所采用的參考橢球元素為

a=6 378 137 m，b=6 356 752，f=1/298.257

地球參考橢球體面是本國大地測量投影和計算的基準面。由于地球橢球體的偏率很小，故當測區較小時，可把地球當作圓球看待，其半徑可取：R=（2a+b）/3，其近似值為6 371 km。

3 確定地球面上點位的幾種坐標系

地面點的空間位置，通常可用該點相對于某基準面和基準線的三維坐標或二維坐標來確定。確定地面點空間位置的幾種坐標系如下。

3.1 地心坐標系

是以總橢球為根據的空間三維直角坐標系，是一個世界統一的理想地心大地坐標系，用于衛星大地測量。

3.2 地理坐標系

是采用以大地水準面和參考橢球為根據的球面坐標系，按投影面的不同，分為天文坐標系和大地坐標系。

3.2.1 天文坐標系

天文坐標又稱天文地理坐標，是用天文經度λ和天文緯度φ來表示地面點投影在大地水準面上的位置。

國際公認通過英國格林尼治天文臺的子午面為首子午面，作為計算經度的起始；并規定自首子午線向東或向西計算，都為0°至180°稱為東經或西經。垂直于地軸的平面與球面的交線稱為緯線。垂直于地軸并通過地球中心的平面為赤道平面，其與地球面相交的線為赤道；某A點的緯度，即為該點的鉛垂線與赤道平面的交角。赤道是緯度的起始線，自赤道向北或向南，都為0°至90°稱為北緯或南緯。

各點的天文坐標(λ，φ),是在各點上用天文測量法獨立測定的。例如北京某點的λ為 東經116°28'，φ為 北緯 39°54' 。

若再顧及地面點超出大地水準面的垂距（海拔高h），那就構成為三維坐標系（λ，φ，h）。

3.2.2 大地坐標系

大地坐標又稱大地地理坐標，是用大地經度L和大地緯度B表示地面點投影在參考地球橢球面上的位置。A點的大地經度L，就是包含A的大地子午面與首子午面所夾的兩面角；A點的大地緯度B,是過A的橢球面法線與赤道平面的交角。各點大地經、緯度的確定方法與天文經、緯度測定的方法不同，它們是根據一個起始的大地點（稱為“大地原點”，該點的大地經緯度與天文經緯度一致）的大地坐標，再按大地測量所得的數據推算而得到的; 這是傳統的方法。

我國的大地原點設立在陜西省涇陽縣，作為全國大地坐標的起算點；由此建立的大地地理坐標系稱為“1980國家大地坐標系”。

地面點超出參考橢球的垂距稱為“大地高H”。若再顧及大地高之值，那也就成為三維坐標（L，B，H）。

近代衛星大地測量的發展，將更多地用GPS方法獲得測點地心坐標系的空間大地直角坐標。經過坐標轉換，也可獲得該點的大地地理坐標L，B，H之值，或其他應用的坐標系統中之值。相對于傳統的方法，可以說是一大飛躍。

3.3 平面直角坐標系

上述的地理坐標系或地心坐標系一般適用于確定高級控制點的定位或作為初始的計算。對于地球上大量的測量、工程放樣、計算和繪圖的工作，則最好是在平面上進行。但地球表面是一個曲面，要把在球面上所測的點位換算到平面上，對全境及大區域而言，就關系到投影的問題。

3.3.1 高斯平面直角坐標

用高斯投影方法把在球面上所測的點位投射歸化到平面上所建立的平面直角坐標系。我國采用高斯投影方法。

3.3.2 地區平面直角坐標

對于局部的小區域，例如某個小城鎮或施工地區，相對地球半徑，這小塊球面可以當作平面看待。可用測區中心的切平面P來代替大地水準曲面，此時在球面上實測的長度D也就不必顧及投影的變化當成是平面上的測量值，直接用于繪圖或計算。

4 地面點的高程

由高程基準面到地面點的鉛垂距離(高度)，稱為該點的高程。若高程基準面是大地水準面，則稱為“絕對高程”或“海拔”。我國由青島驗潮站經多年觀察所確定的“黃海平均海水面”作為大地水準面，其高程為零。為此，國家在青島一個穩固的山洞里設置了“國家水準原點”，測得該點到黃海平均海水面的高度為72.260 m，即青島國家水準原點的高程為72.260 m。全國性統一的絕對高程系，就是從青島國家水準原點出發建立的。

在局部地區，為工程設計及施工放樣的方便，有時就設定某個高度的水準面作為該地高程基準面，由此所得的高程值稱為“相對高程”或稱“假定高程”。

地球曲率對于投影到水平面上距離的誤差影響，在半徑為10 km的測區范圍內是可以忽略的。那末地球曲率對于高差測量的誤差影響又如何呢？以水平面代替地球水準面而產生的高程誤差以Δh表示，則

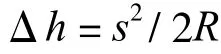
式中：s— 地面上距離；

R— 地球平均半徑（R= 6 371 km）。由此可知，當s為1 km時，其高差誤差Δh就會有8 cm。從而，在小區域對點的平面位置測量時可不顧及地球曲率的影響，但進行點的高程測量時，對于地球曲率的問題是常常要顧及的。