凸輪評定公差標準及評定方法

/ 廣州威而信精密儀器有限公司西安分公司

0 引言

要做到高準確度、高效率地測量發動機凸輪的各項參數，并對各項測量參數進行正確處理、評定，及時快速地反饋凸輪的質量信息，傳統的光學機械量儀以及人工數據處理的方法，已不能適應凸輪廣泛采用自動線高效生產的需要了。隨著汽車工業的高速發展和制造技術的不斷提高，對凸輪準確度的測量也必須相應地配套高效率的凸輪綜合自動測量儀，并配以快速的數據處理、評定軟件及打印輸出功能。這里應特別強調的是，評定公差的標準應與凸輪的功能要求相適應。

1 凸輪升程曲線函數式的構建

凸輪機構從動件的運動規律，是通過凸輪正確形狀的旋轉運動取得的。因此，凸輪機構設計過程中，必須根據從動件（挺柱）的運動要求，正確設計凸輪的升程曲線。如圖1所示，理論上要求凸輪升程曲線應以連續函數的形式給出，即

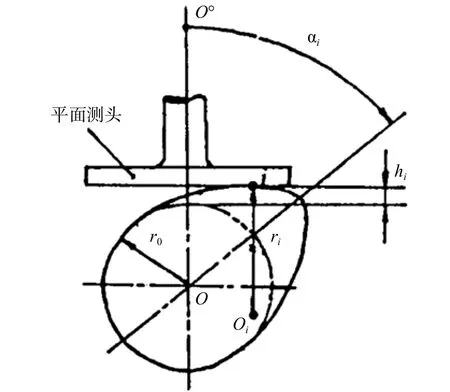
圖1 凸輪升程函數式的建立

式中：h— 凸輪被測點的升程；

α— 凸輪被測點的轉角；

r— 凸輪被測點的曲率半徑。

在凸輪機構工作過程中，理論上要求凸輪不出現“剛性沖擊”和“柔性沖擊”[1]，這就必須保證凸輪升程曲線二階連續可導。但實際應用中，凸輪的升程曲線一般不用連續函數來描述，而是把凸輪的理論升程曲線用“升程表”的形式給出。升程表給出的是一組離散數據，數據的多少依據凸輪的工作要求確定（一般是1°間隔給出一個理論升程值）。凸輪從動件的運動準確度，即凸輪升程曲線的準確度，由凸輪的升程公差來控制。

2 凸輪評定采用的公差標準

目前，參照GB/T 1182-2008《產品幾何技術規范（GPS） 幾何公差形狀、位置和跳動公差標注》凸輪有（可采用）以下公差標注方法：

1）按尺寸公差要求標注；

2）按幾何公差要求標注：

（1）采用線（面）輪廓度公差標注，

（2）采用徑向圓跳動公差標注。

3 對凸輪采用尺寸公差評定的認識

凸輪用尺寸公差評定，測量的是凸輪的升程變化量，盡管控制方向符合凸輪測量實際，評定簡單、方便、直觀，但依據GB/T4249-2009《產品幾何技術規范（GPS）公差原則》，尺寸公差并不控制凸輪的形狀誤差，所以，在建立了幾何公差國家標準之后，凸輪應采用幾何公差評定。

凸輪測量屬于形位誤差的測量范疇，如果用尺寸公差控制，因為尺寸公差帶的位置是固定的，不隨凸輪實際形狀浮動（圖2），按照國家標準GB/T16671-2009《（GPS）-幾何公差 最大實體要求最小實體要求和可逆要求》的要求，在建立了幾何公差國家標準之后，仍用尺寸公差評定凸輪升程誤差的方法是欠妥當的，它往往可能引起誤判。

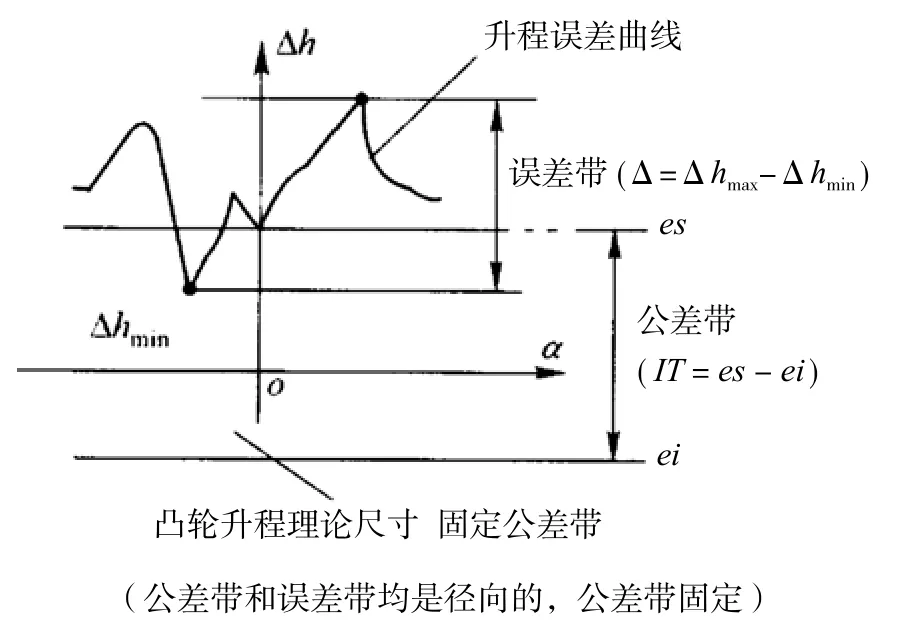
圖2 采用尺寸公差評定凸輪的公差帶與誤差帶

4 對凸輪采用輪廓度公差評定的看法

線（面）輪廓度公差帶是包絡一系列直徑為公差值的圓的兩包絡線之間的區域，諸圓的圓心應位于凸輪的理想輪廓上。對凸輪而論，其理想輪廓是指以凸輪升程理論正確尺寸所描述的輪廓。

線（面）輪廓度公差帶所控制的區域，是凸輪的法向變化量，而凸輪的誤差（測量）值是徑向變化量（圖3）。用線（面）輪廓度公差控制凸輪的誤差，盡管公差帶的位置可隨凸輪的實際形狀浮動，但評定時，必須將凸輪誤差（測量）的徑向值轉化為法向值，才能和公差值進行比較，測量和評定效率不高。所以，采用線（面）輪廓度公差評定凸輪的方法是有待商榷的。

圖3 采用線輪廓度公差評定凸輪的概念

5 推薦凸輪采用徑向圓跳動公差評定

徑向圓跳動公差帶是在垂直于基準軸線上任意測量平面內半徑為公差值、且圓心在基準軸線上的兩個同心圓之間的區域。對凸輪而言，正好符合凸輪測量的實際方法。

測量時，以凸輪的基圓中心軸線為基準軸線，可以這樣來理解凸輪升程的測量值：凸輪輪廓上每一個升程測量點的運動軌跡，都是凸輪基圓的同心圓，當實際被測點偏離同心圓時，這個偏離值就是凸輪被測點的徑向圓跳動誤差——被測點的升程偏差（圖4）。凸輪輪廓上所有升程測量點中，徑向跳動量的最大值與最小值之差，就是凸輪升程的最大變動量，即被測凸輪的升程誤差。

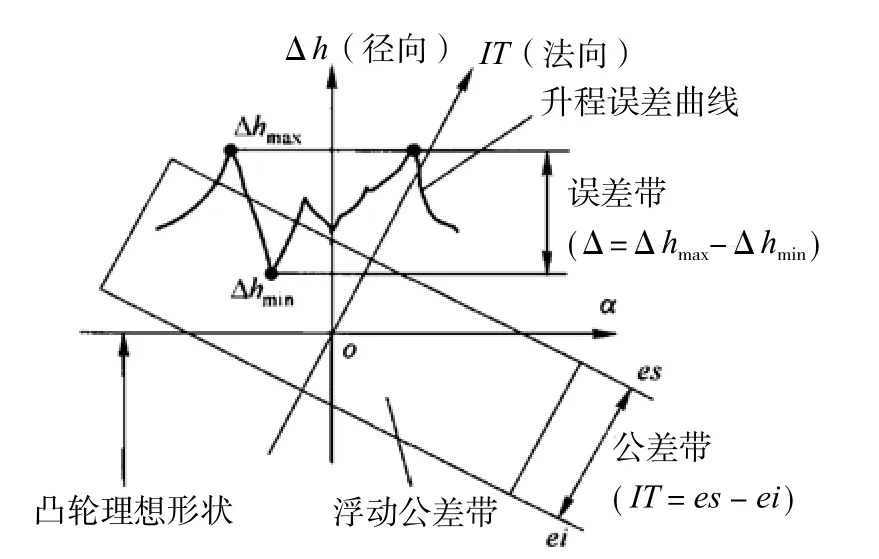
圖4 采用線輪廓度公差評定凸輪的公差帶

根據標準，徑向圓跳動公差可以控制全部要素或部分要素，則可按凸輪的功能要求，對凸輪的基圓段、升程段、降程段、過度段、緩沖段……分別給予不同的公差要求。

用徑向圓跳動公差控制凸輪的升程誤差，可以彌補尺寸公差和線（面）輪廓度公差控制方法的不足：徑向圓跳動動公差控制的是凸輪的徑向變化值，凸輪測量的也是徑向變化值，兩者一致，且公差帶的位置隨凸輪的實際形狀浮動（圖5）。當凸輪實際偏差具有確定值時，公差帶也具有確定的位置，即公差帶的位置由凸輪的實際偏差確定（圖6）。

用徑向圓跳動公差評定凸輪時，測量值和公差都是徑向值，便于比較、測量，評定簡便、直觀。

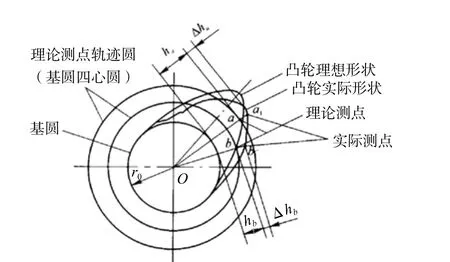
圖5 對徑向圓跳動應用于凸輪評定

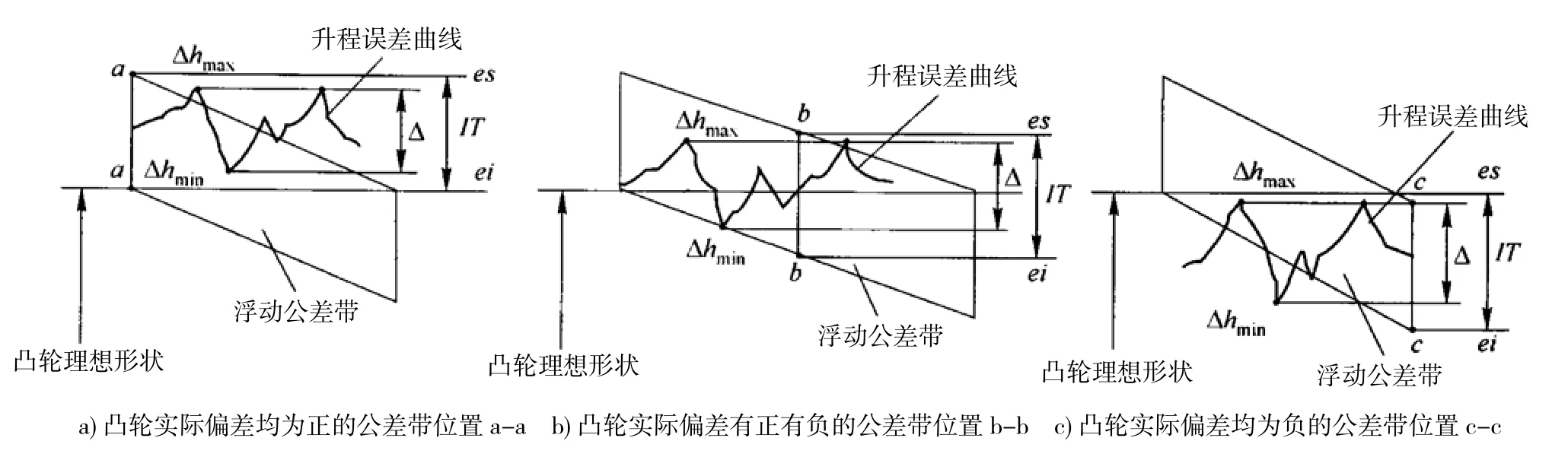
圖6 采用徑向圓跳動公差評定凸輪的公差帶與誤差帶（公差帶和誤差帶均是徑向的，公差帶浮動）

6 凸輪的升程誤差與形狀誤差

凸輪的升程誤差和形狀誤差既有聯系又有區別[2-5]。雖然采用的是同一測量數據，但它們的處理方法不同。凸輪升程誤差與凸輪形狀誤差是兩個不同的概念。如圖7所示，凸輪升程誤差屬于尺寸公差的范疇，其公差帶的位置由凸輪升程的理論尺寸確定，且公差帶的位置是固定的。凸輪升程公差控制要素為凸輪機構從動件的實際位移相對于理論位移的變動量（實際凸輪輪廓尺寸誤差）；凸輪形狀誤差屬于幾何公差范疇，公差帶的方向隨凸輪實際形狀而定，公差帶的位置是浮動的，幾何公差控制要素為實際凸輪的形狀誤差。形狀誤差的大小應按“最小條件”要求來確定。

凸輪機構從動件的運動規律是通過凸輪的形狀來反映的，因此需要根據從動件的運動要求設計凸輪的形狀。一般來說，每個凸輪的形狀都是由基圓和許多二次曲線、三次曲線及圓弧等組成，其構成的封閉曲線稱為升程曲線。由于凸輪升程曲線的特殊性，實際應用中提供給加工和測量的升程曲線是0～360°的離散數據，這就是描述每個凸輪形狀的理論升程表，其升程曲線的準確度由升程公差進行控制。

圖7 凸輪的升程誤差與形狀誤差

7 凸輪升程的測量、數據處理、誤差評定

凸輪的升程誤差是指：實際凸輪對應理論角度上的實際升程與理論升程的代數差。即

根據升程誤差的定義，凸輪升程測量時，測量的應是凸輪理論轉角對應測點的實際升程。這一點在實際測量中是不容易做到的，測量數據中一般含有轉角誤差（系統性誤差），必須剔除測量數據中的轉角誤差的影響，才可能得出正確的測量結果。這就提出了如何進行凸輪測量和數據處理方法的問題[6]。

如圖8所示，凸輪升程表上給出的是理論轉角α對應的理論升程h，按定義要求，本應測量出理論轉角α對應測點的實際升程hs(圖8a)。可是，由于凸輪測量起點轉角有誤差Δα，實際上測量出的不是理論轉角α對應點上的實際升程hs，而是轉角α+Δα對應點上的實際升程hΔα(圖 8b)。所以，一般按公式

求解的升程誤差與定義是不相符合的。

圖8 凸輪的設計要求與測量現狀

符合定義的升程誤差，應按下式求解：

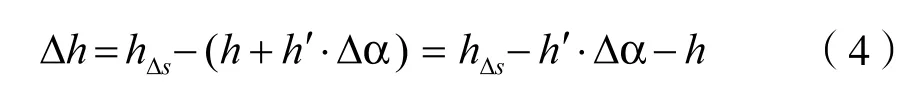
式中：h′ = dh/dα— 凸輪升程變化率；

Δα— 應根據凸輪的公差要求分別求解。

凸輪測量（處理）方法應是：①獲得原始（迭代）數據，要求測量數據盡量準確；②對原始數據進行處理，只有準確的原始數據，才能保證數據處理的可靠性；③根據處理結果確定（計算出）各凸輪測量起始點位移量（起始轉角的角度誤差）Δα（用它來進行優化處理，亦用來修正凸輪的相位角）。

如果凸輪升程符合公差要求，則直接將升程判為合格；如果升程出現某些超差點，這時應將升程誤差和升程公差要求統籌考慮，進行數據處理，再給出凸輪升程合格與否的結論[6]。

為此，建立目標函數

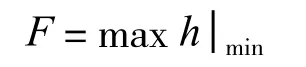
進行優化處理，直至目標函數F為最小。

具體方法：從升程的迭代數據中，找出升程誤差曲線上的凸輪升、降程段（左、右側）升程誤差最大點a和最小點c、d，根據“等距準則”可得等距方程式

解上列方程式，可得

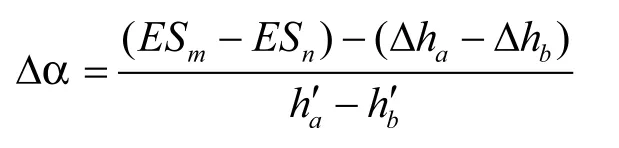
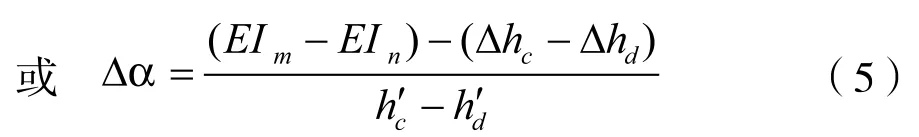
數據處理后的升程誤差為

升程誤差曲線的最小包容區域的寬度為

一般應根據凸輪升程的公差要求，給出相應的處理方法。數據處理過程，就是將測量數據處理成符合定義的升程誤差值——符合設計要求的升程誤差值的過程。

當凸輪的升程公差按尺寸公差標注時，公差帶的位置是固定的。只要求測量數據能保證凸輪升程最大限度的合格，不考慮誤差帶包容區域的最大寬度為最小，即不考慮“最小條件”要求。

當凸輪的升程公差按幾何公差標注時，公差帶的位置是浮動的。必須根據實際凸輪誤差數據，首先確定公差帶的位置，并應保證誤差帶的形狀和公差帶的形狀相一致，誤差包容區域的最大寬度為最小。即凸輪的升程誤差應符合“最小條件”要求[7]。

凸輪升程誤差曲線符合“最小條件”要求的評定準則：

1）凸輪左右側高點等值準則——準則一（圖9）

（1）凸輪左右側誤差最高點相等（定浮動公差帶上限的位置），即

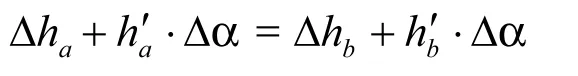
由上列方程式解出

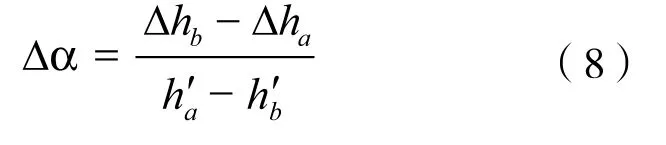
圖9 高點等值準則

（2）凸輪誤差最低點(取左右側誤差最低點中的較低者) 的升程變化率的絕對值在左、右側誤差最高點的升程變化率的絕對值之間，即

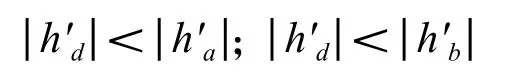
2）凸輪左右側低點等值準則——準則二（圖10）

（1）凸輪左右側誤差最低點相等（定浮動公差帶下限的位置），即

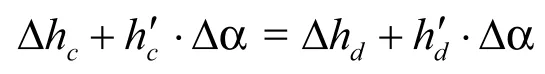
由上列方程式解出

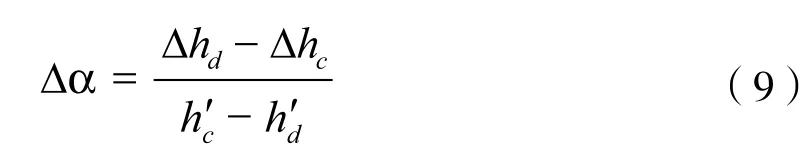
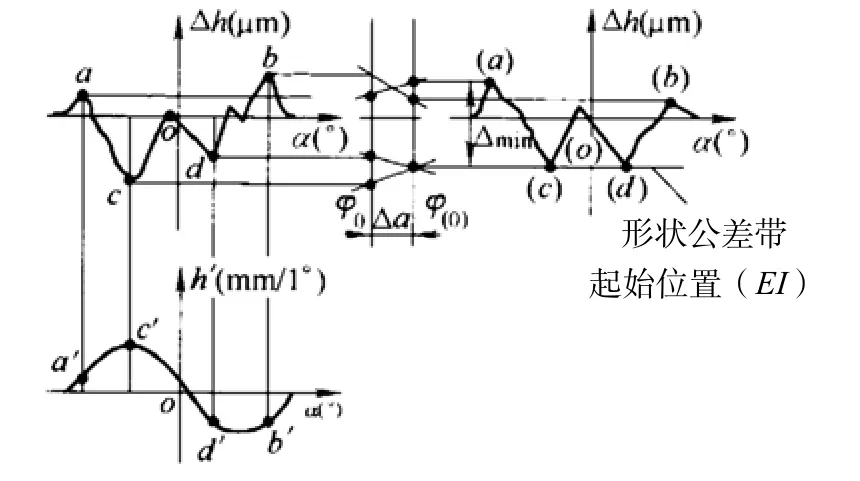
圖10 低點等值準則

（2）凸輪誤差最高點（取左右側誤差最高點中的較高者）的升程變化率的絕對值在左、右側誤差最低點的升程變率的絕對值之間，即

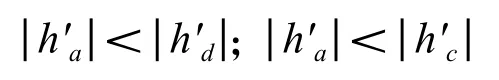
3）凸輪公差小的一側高點零距準則——準則三（圖11）

（1）凸輪公差小的一側左側(或右側）誤差最高點a(或b)落在公差帶ESm(或ESn)上，即

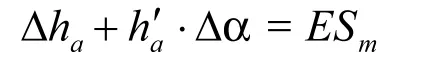
由上列方程式解出

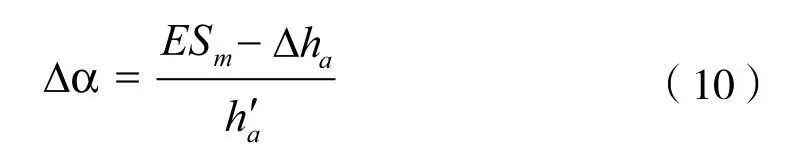
（2）凸輪誤差最低點(取左右側誤差最低點中的較低者) 的升程變化率的絕對值在左、右側誤差最高點的升程變化率的絕對值之間，即

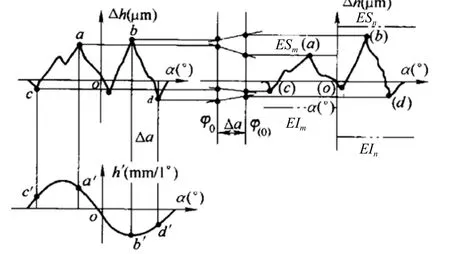
圖11 高點零距準則

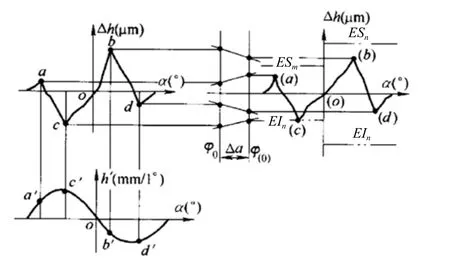
圖12 低點零距準則

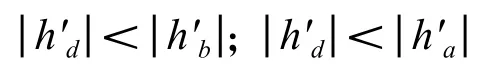
4）凸輪公差小的一側低點零距準則——準則四（圖12）

（1）凸輪公差小的一側左側（或右側）誤差最低點c（或d）落在公差帶EIm(或EIn)上，即

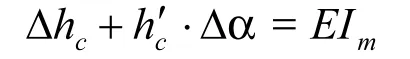
由上列方程式解出

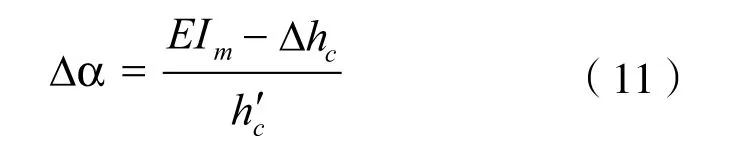
（2）凸輪誤差最高點（取左右側誤差最高點中的較高者）的升程變化率的絕對值在左、右側誤差最低點的升程變率的絕對值之間，即

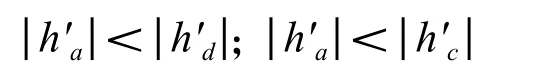
用“反證法”證明了以上各“準則”的正確性。

當升程公差按幾何公差標注時，只給出了公差值的大小，應根據準則一、準則二來確定凸輪升程公差帶的位置和浮動方向，并保證了誤差帶的形狀和公差帶的形狀相一致，誤差包容區域的最大寬度為最小；當升程公差按尺寸公差標注時，公差值的大小和公差帶的位置是確定的，應根據準則一、二（用于左、右側公差相等），準則三、四（用于左、右側公差不相等）來確定凸輪誤差點相對于公差帶的位置，并做到了最大限度地保證凸輪升程合格。

具體計算（求解）方法如下：

（1）與凸輪公差要求相適應的凸輪實際測量位置的起始轉角為

式中： — 按“敏感點法”求解；

—凸輪起點轉角誤差，根據要求分別由式（8）～（11）解出。

（2）按“最小條件”評定的凸輪升程誤差值，按下式求解

式中：Δhi、Δh(i)— 坐標旋轉前、后的升程誤差值。

最后應指出，凸輪升程公差按幾何公差標注時，凸輪左、右側等值誤差最高（最低）點構成升程誤差曲線的上（下）包容直線，誤差最低（最高）點構成下（上）包容直線，上下包容直線間的距離，就是凸輪升程誤差曲線的包容區域的寬度Δ，即按“最小條件”評定的凸輪升程誤差值：

這時，凸輪升程誤差曲線上被測點的誤差值Δh(i)符合“最小條件”要求。

凸輪的升程公差，一般常見兩種標注方法[2]：①尺寸公差標注方法——標注的是一個沒有（不冠）符號（數學性質）的絕對值。無論公稱尺寸是多大，它的上下兩個極限偏差均為正、均為負、一正一負、一正一零、或一零一負，其公差是允許尺寸的變動量（絕對值）。公差帶的位置由凸輪升程的理論正確尺寸確定，且公差帶位置是固定的，升程公差控制的僅是實際凸輪的輪廓尺寸。這時，凸輪的升程誤差應按尺寸公差來處理：凸輪的升程公差要求，設定了兩個極限尺寸——最大實體尺寸（MMS）和最小實體尺寸（LMS）來限制升程的實際尺寸，要求凸輪升程的任一局部尺寸不得超出兩個極限尺寸；②幾何公差標注方法——標注的是不提取（實際）被測要素對其理想要素的允許變動。其公差帶是提取（實際）被測要素對其理想要素允許變動的區域。方向隨凸輪的實際形狀而定（變動），公差帶的位置是浮動的，升程公差控制要素是實際凸輪的輪廓形狀。這時，凸輪的升程誤差應按幾何公差來處理（升程誤差的測量數據，應按“最小條件”要求進行評定）：凸輪的升程公差要求，設定了兩個平行（或等距）的界線或界面，構成幾何公差帶來限制實際被測要素。

凸輪測量數據按尺寸公差要求處理，把升程誤差與升程公差聯系了起來，最大限度地保證了凸輪升程的合格（圖13）；凸輪測量數據按幾何公差要求處理，把升程誤差與“最小條件”聯系了起來，保證了凸輪升程誤差（包容區域的寬度）的最大值為最小（圖14）。處理時可根據設計要求，選擇相應的處理方法。

圖13 凸輪測量數據按尺寸公差要求

圖14 凸輪測量數據按幾何公差要求

在高效率的凸輪綜合自動測量儀上，進行凸輪升程測量時，凸輪每轉過18″軟件就給出一個升程測量值，經數據處理后，軟件按每1°輸出測量結果（升程誤差值、升程誤差曲線）。

8 結語

對于凸輪來說，應該分別標注尺寸（升程）公差和幾何公差。因為可以將同一測量數據，分別處理成升程（尺寸）誤差和形狀誤差，這樣標注更切合凸輪實際。

避免了用升程（尺寸）公差控制凸輪形狀誤差時，如將凸輪升程處理為合格，則包容區域的寬度不為最小；如將包容區域的寬度處理為最小，則凸輪的升程超差，與凸輪升程合格的結論相矛盾。

本文介紹的凸輪測量數據的處理過程，把凸輪的升程誤差與升程公差聯系了起來，最大限度地保證了凸輪升程的合格；同時，凸輪測量數據的處理過程，也把形狀誤差與“最小條件”聯系了起來，保證了形狀誤差（包容區域的寬度）的最大值為最小，兩者分別評定，各自滿足，互不干涉。

最后，推薦采用徑向圓跳動公差進行凸輪評定（控制），以彌補尺寸公差和線（面）輪廓度公差控制方法的不足。

[1]管榮法.凸輪與凸輪機構[M].北京：國防工業出版社，1993.

[2]劉巽爾.《GB/T1182-2008》簡介（續一）[J].機械工業標準化與質量，2009（6）：20-25.

[3]劉巽爾.《GB/T1182-2008》簡介（續二）[J].機械工業標準化與質量，2009（7）：25-31.

[4]劉巽爾.《GB/T1182-2008》簡介（續三）[J].機械工業標準化與質量，2009（8）：32-35.

[5]劉巽爾.《GB/T1182-2008》簡介（續四）[J].機械工業標準化與質量，2009（9）：25-32.

[6]劉興富，李長星.發動機凸輪軸檢測方法綜述[J].計量技術，2005（8）：27-30.

[7]劉興富.發動機凸輪升程誤差符合“最小條件”的評定準則[J].標準化報道，1997（9）：17-22.