城市軌道交通多路徑選擇研究

趙 楠，李 超

（中國鐵道科學研究院 電子計算技術研究所，北京 100081）

1 研究背景

目前，深圳軌道交通網絡由 5 條線路構成，合計里程 178 km，分別由 3 家不同的運營公司共同管理運營。在無障礙換乘的模式下，如何既能保證整個地鐵系統一體化運營，又能公平、公正地維持各運營商的利益，是多家運營商合作的前提，因此要求地鐵總公司有一套合理的清分制度保障其正常運營。而路網中有效路徑的選擇及其對客流的承擔比例是地鐵清分的重要基礎數據，也是地鐵中心分配票款的重要依據。本文結合深圳地鐵具體情況及調研結果，重點介紹深圳地鐵軌道交通多路徑選擇模型算法及模型參數標定。

2 深圳地鐵布局

深圳地鐵開通運營線路如圖 1 所示，5 條線路形成網狀連接，其中 1 號線、2 號線和 5 號線分別由西北、東北向東橫穿城市；3 號線、4 號線由北向南縱貫城市。車站編號的順序為從 1 號線到 5 號線，共 118 個車站，其中換乘站 13 個。由于換乘站較多，乘客從某車站出發到達另一條線的其他車站有多種選擇路徑。綜合考慮列車發車間隔、旅客換乘步行時間、列車運行時間和車站停車時間等因素，可初步確定車站間的有效路徑；根據建立的模型可計算出兩個車站間不同有效路徑的旅客比例，并將此數據提交地鐵清分中心提供清分依據。

3 路徑選擇因素分析

在無障礙換乘的模式下，影響城市軌道交通運費清分的因素多而復雜，可以概括為旅客本身因素、旅客出行特征因素、軌道交通網絡因素和其他方面的因素。每一影響因素又包括很多的具體指標，如旅客本身因素主要包括年齡等；出行特征因素主要包括出行距離、出行目的和是否高峰出行等；網絡因素主要包括線網結構、出行時間、路徑換乘形式和運營時間等；其他方面因素主要包括票價和對運營商的偏好等。其中，旅客出行特征因素作為關鍵因素，主要包括以下指標。

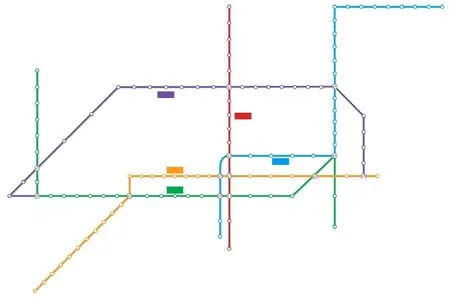
圖1 深圳地鐵線路圖

（1）出行距離。出行距離是指旅客一次軌道交通的出行距離。不同的出行距離對旅客選擇路徑具有一定的影響。例如，長距離出行時，旅客一般希望能夠通過換乘來節約總出行時間；而對于短距離出行，旅客一般都不希望換乘。

（2）出行目的。不同出行目的旅客對路徑的選擇也不同。例如，以購物、休閑、游玩為目的的旅客一般不會太在意出行時間的長短，而更重視出行中的方便舒適度；而上下班或公務出行時旅客對時間比較敏感，更希望能夠通過換乘來節省總出行時間。

（3）出行時段。出行時段包括客流高峰與平峰時段。在客流高峰時段，由于上下車人數很多，車廂內和車站的旅客也很多，很難保證一次候車就有機會上車，而且每次換乘時上下車不方便，還有可能需要步行一段距離，消耗體力和時間，因此，旅客希望選擇換乘次數少的路徑，對于時間的敏感度不是很高。

（4）擁擠程度。擁擠程度主要是指路徑的平均擁擠程度。該因素影響旅客對于出行路徑的選擇，進而影響運費清分。在深圳市旅客出行調查中，13% 的人選擇擁擠程度為最重要的因素。在清分模型中可以采用列車的容納能力和需要服務的旅客總量的比例來量化此因素。

通過對深圳地鐵的 2 000 份問卷調查可知，48% 的旅客會選擇總出行時間最短的出行方式，42% 的旅客會選擇換乘時間最少的出行方式，5%的旅客會選擇經過站點數最少的出行方式。由調查數據可知，旅客出行路徑選擇關注的最重要因素是總出行時間最短和換乘次數最少，較重要因素是擁擠程度，這 3 項因素是構建模型的主要參數指標。

4 模型構建

目前，模型主要有正態分布概率模型和 Logit模型。結合深圳地鐵實際情況，在對比正態分布概率模型和 Logit 模型后，發現采用正態分布概率模型時的測算結果更符合深圳地鐵的調查問卷結果，以下主要介紹基于正態分布的多路徑模型。

4.1 ??正態分布概率模型

路徑的選擇概率是以各路徑的修正綜合阻抗值為基礎，按照一定的統計規律，確定各有效徑路分擔某一 OD 客流的比例。①當有效路徑集的元素惟一時，該有效路徑是惟一的絕對最優解，承擔100%的客流。②當有效路徑集的元素不惟一時，就產生了客流如何在各條路徑中分配的問題，基本理念是根據旅客選擇路徑的概率計算客流的路徑分配比例。

（3）1≥P1≥P2≥…≥Pk≥0，即阻抗值越大的路徑被選擇的概率越小，其中最小阻抗值路徑被選擇的概率最大。

（5）隨著阻抗值的增加， Pi的遞減速率將迅速增加，即路徑被選擇的概率將迅速減少。實際上，旅客對乘坐時間的較大延長會比較敏感。

概率計算中常用的正態分布函數能夠很好地滿足上述要求，其函數公式為：

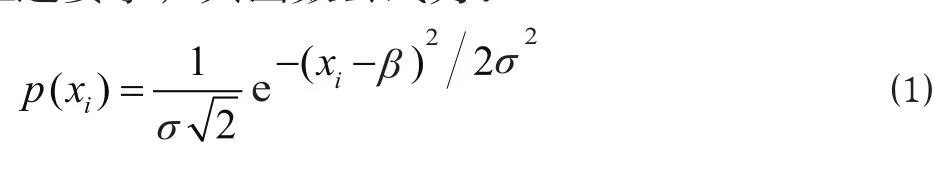
式中：β 為得到概率最大期望的 x 值，在這里為 0；e 為自然對數的底，約等于 2.718；σ 是一個常數，其值決定正態曲線的變化程度。隨機變量 xi取為其中 ：α?為旅客在出行過程中對換乘時間的敏感度；μ 為旅客在出行過程中對出行時間的敏感度；為第 i 條有效路徑的換乘時間，min；為第 i 條有效路徑的總出行時間，min。由于不可能權值小于最小阻抗值min的路徑，因此，只需要取正態分布曲線x≥μ的正半部分。

σ是公式中的參數，對于所有 OD 對是一個常數。它在數學上的意義非常明確，但是很難直接賦予某種實際意義。可以通過實際旅客出行路徑選擇的交通調查結果分析擬合出參數σ的值。則路徑的分配比例可用以下公式計算：

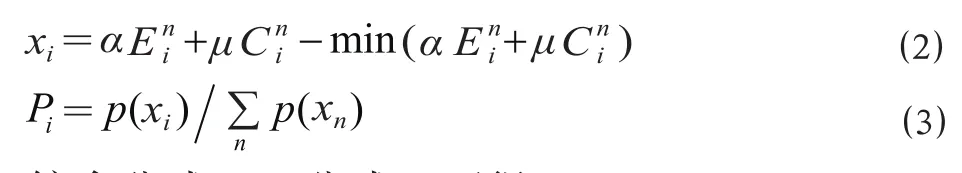
綜合公式⑴～公式⑶可得：

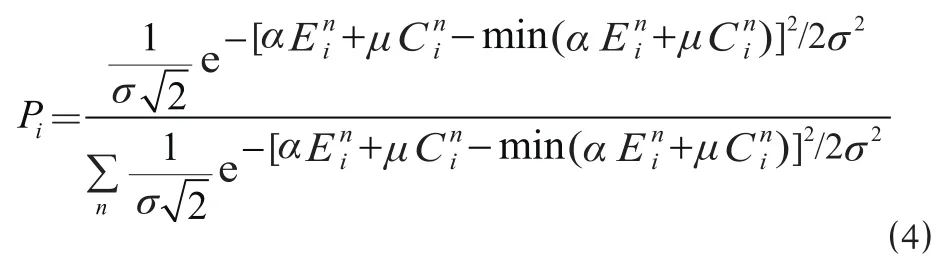
通過選擇合理的σ參數，采用公式⑷的概率分布函數可更加接近實際地反映旅客的路徑選擇行為，而且能夠適應 OD 對之間有效路徑的不同數量和組合類型，滿足Pi的上述 5 個特性。

4.2 ??正態分布概率模型參數標定

在正態分布概率模型中，需要標定的未知參數為α、μ、σ。其中，σ反映了旅客在實際選擇有效路徑時，具有出行時間越短旅客選擇概率越大，出行時間增加時路徑被選擇的概率明顯下滑的規律；而α表現出換乘會減少選擇概率的現象。在標定時利用深圳市旅客軌道交通出行選擇情況，參數值如表 1 所示。

根據表 1 調查數據驗證路徑選擇概率模型的有效性，統計擬合參數如表 2 所示。

為驗證正態分布模型及其參數估計的有效性，利用實際調查數據與模型計算結果進行比照，結果如表 3 所示。

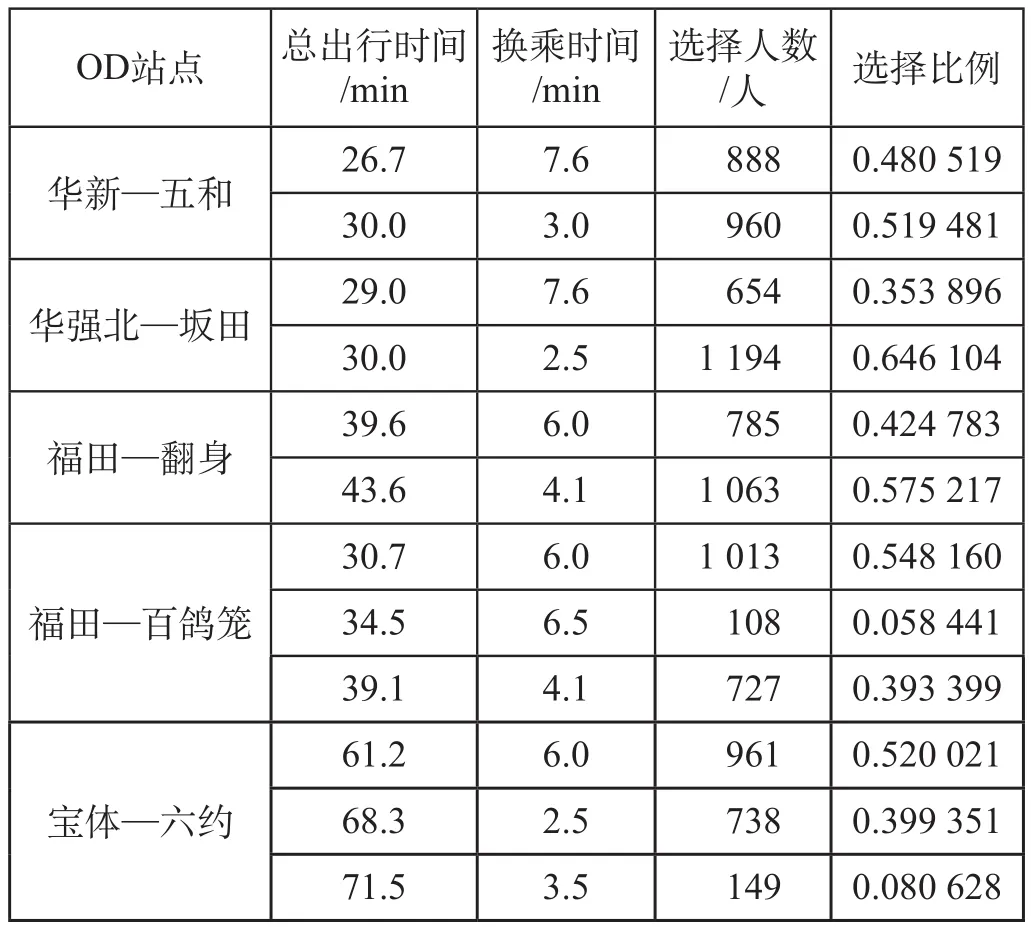
表?1? 不同出行距離和出行時段條件下旅客路徑選擇參數值表

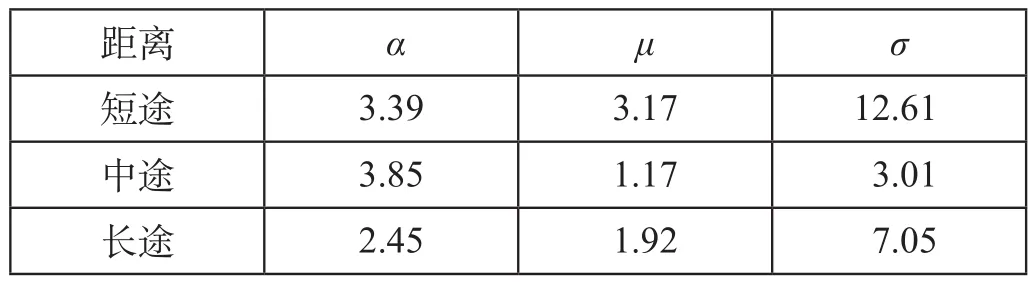
表?2? 正態分布參數表

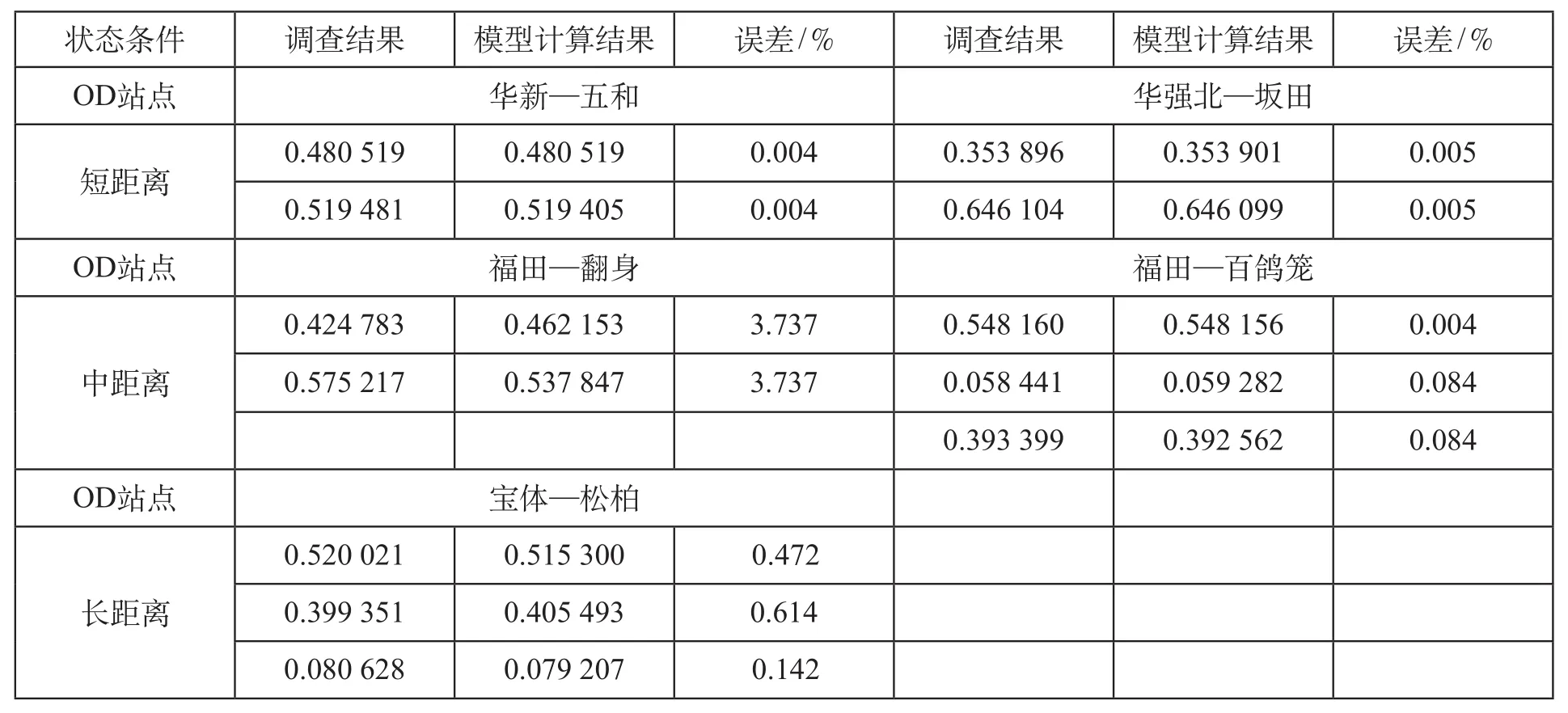
表?3? 交通調查與正態分布概率模型預測計算對照分析表

從實際交通調查結果與正態分布模型預測計算的對照分析表可以看出，在 OD 站點中，計算結果與調查結果偏差最大的是華強北—坂田，誤差為 3.737%；偏差最小的是華新—五和，誤差為0.004%。總體來看，誤差率不大于 4%，說明模型測算得到的路徑分擔比例與實際的擬合度達到96%，符合實際應用需求。

4.3 模型參數分析

深圳地鐵多路徑選擇模型采用的是正態分布概率模型，在算法中 α、μ、σ?的變化直接影響選擇結果，通過對典型 OD 對分析比照，對有關因素進行了靈敏度分析，旨在準確把握當某些影響因素發生變化時，各家運營商的清分比例變化情況。

根據調研數據和模型計算表明，當 α 的取值越來越大時，換乘時間長的有效路徑的分配比例將會下降；反之，分配比例將會上升。當 μ 的取值越來越大時，出行時間越長的有效路徑的分配比例將會下降；反之，分配比例將會上升。當 σ 的取值越來越大時，分配比例越大的有效路徑的分配比例將會下降；反之，分配比例將會上升。

5 結束語

各個有效路徑的旅客分擔比例是地鐵公司進行清分票款的主要依據，通過模型算法開發出一套切實有效的多路徑比例計算軟件，并投入實際應用。如何繼續改進模型算法，使之能適用于更多的城市軌道交通系統，并能更準確地計算城市的有效路徑分擔比例，為地鐵公司清分系統提供確實有效的基礎數據是值得深入研究的方向。