石灰石CO2循環特性神經網絡預測

陳鴻偉， 閆 瑾， 危日光， 高建強， 黃新章

（1.華北電力大學 能源與動力工程學院，保定071003；2.沈陽工程學院 能源與動力工程系，沈陽110136）

以化石燃料為原料的能源生產工業，其CO2排放量已占全球總排放量的30%以上.因此，有效減少能源工業中溫室氣體排放成為急需解決的重要課題［1］.目前最可行的減排方法，是利用固態吸收劑捕捉和分離煙氣（或氣化氣）中的CO2，然后將得到的高濃度CO2氣體液化后注入地質處置層或深海［2］.采用鈣基吸收劑作為CO2捕集循環中的載體，化學過程簡單，成本低廉且可有效避免CO2捕捉過程中的熱動力損失，但是還存在亟待解決的實際應用問題.其中關鍵問題就是要解決循環反應過程中顆粒燒結引起煅燒后顆粒表面形貌、微顆粒結構以及孔隙結構的惡化，因為孔隙比表面積和孔容積減小會導致鈣基吸收劑活性的衰減［3－4］.

為了獲得CO2吸收效率的最大值，科研工作者開展了大量鈣基吸收劑煅燒和碳酸化循環反應特性研究：包括熱重分析或固定床試驗，或給定通用顆粒模型預測吸收劑顆粒反應能力.但是，如果采用單一的試驗方式，則參數的設定會受到試驗設備本身的限制且難以消除試驗誤差；雖然顆粒預測模型可以反映轉化率的變化趨勢，但吸收劑的顆粒特性以及反應條件卻無法通過方程參數體現［5－6］.因此，在鈣基吸收劑CO2的循環過程中，需要對各個反應參數在循環過程中吸收劑活性變化的影響作進一步深入研究.神經網絡算法作為一種智能仿真模擬工具，以其特有的高容錯自組織和高度非現性描述等功能，為因反應機理復雜或缺乏有效數據而不能采用半經驗公式的化學反應過程進行直觀、準確的數學模擬提供了新思路，并已廣泛應用于化學工業中的復雜計算和難以確定反應模型的化學反應中［7－9］.

筆者應用熱重分析試驗獲得的鈣基吸收劑CO2循環反應過程曲線作為訓練、測試樣本，并利用基于Levenberg－Marquardt法優化的BP神經網絡來描述具有眾多非線性影響參數作用的CO2循環特性.影響吸收劑活性的參數包括循環次數、顆粒粒徑、煅燒溫度、煅燒時間、煅燒氣氛以及碳酸化時間.在反應動力學區域和擴散區域，筆者采用同一數學模型.

1 試 驗

1.1 試驗樣品

筆者采用X射線熒光光譜分析儀對石灰石樣品進行了成分組成分析（見表1）.樣品篩分后可以得到4組粒徑分布的樣品顆粒：38～48μm，48～62μm，62～80μm和80～180μm.

1.2 TGA試驗

筆者采用 Mettler Toledo TGA／DTA Star熱重分析儀（TGA）進行了鈣基吸收劑煅燒和碳酸化循環反應，并通過與其連接的控制設備和計算機終端對試驗過程進行監控，同時應用流量控制系統對反應氣體的開閉和體積流量進行控制.

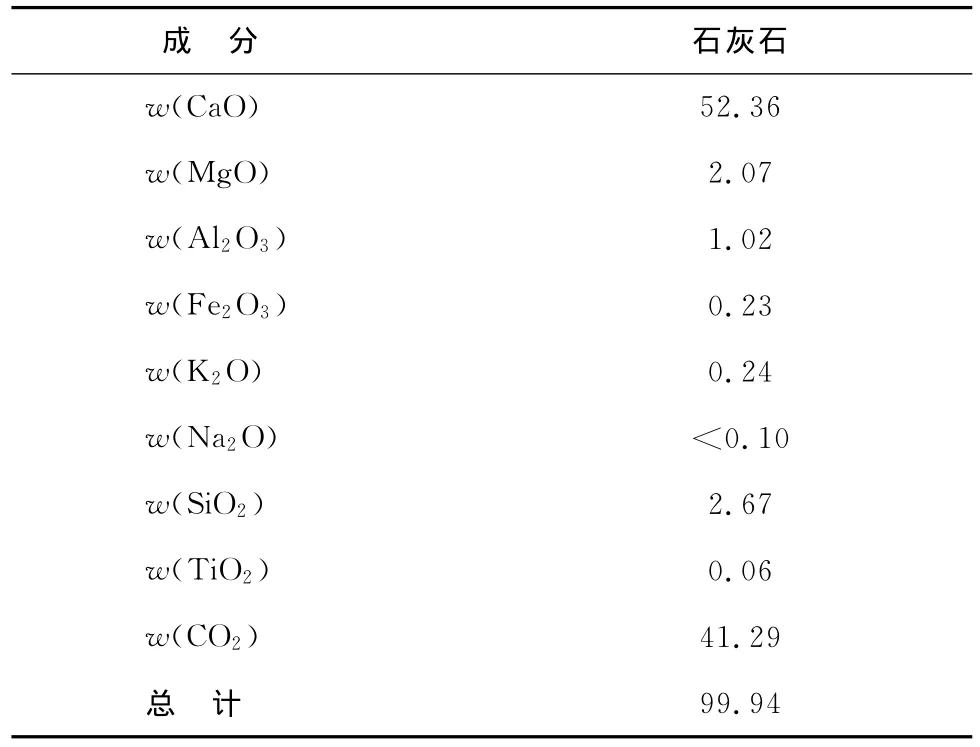
表1 試驗用鈣基吸收劑樣品的成分組成Tab.1 Chemical analysis of the calcium－based sorbent tested%

考慮到熱效應，采用鋁制樣品盤秤取8mg±0.5mg樣品并放入反應器中，以20K／min的升溫速率加熱至預先設定的煅燒溫度，通入反應氣體并加以保溫，以達到充分的煅燒.為保證反應器內稱重系統的穩定性和足夠的反應氣體流量，通入反應器內的恒定氣體流量為50cm3／min.樣品在TGA中進行煅燒和碳酸化循環時保持碳酸化反應條件為650℃、保溫20min，反應氣氛為15%φ（CO2）（N2平衡）.試驗設定的循環次數為20次，并實時采集樣品的質量變化數據.假設樣品質量的變化僅由碳酸鈣的分解與再生造成，依據樣品的質量變化曲線計算樣品的碳酸化轉化率曲線.

2 神經網絡的模擬過程

神經網絡是由大量功能簡單的神經元通過有嚴格規律的拓撲結構組織構成群體并行式處理的計算結構（見圖1）.神經網絡輸入（x1，x2，…，xi）與隱含層權重矩陣Whid相乘，乘積與隱含層閾值向量求和，再經隱含層激活函數Qh傳遞得隱含層神經元輸出（y1，y2，…，yj）.隱含層輸出Yhid與輸出層權重矩陣Wout相乘，乘積與輸出神經元閾值Bout相加，再經函數Qo激活后得到網絡輸出Yout.

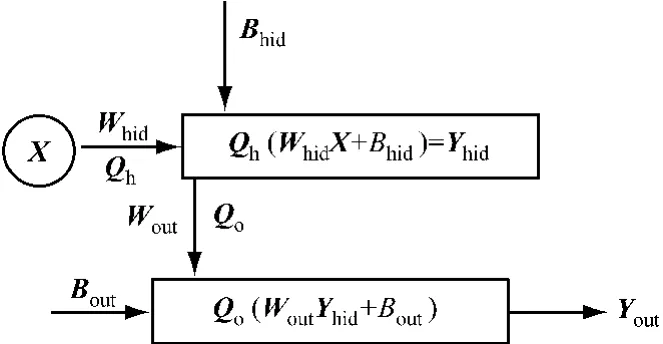
圖1 人工神經網絡拓撲結構Fig.1 Topological structure of a typical artificial neural network

實現信號準確傳遞的關鍵是權重矩陣.一般，采用試驗數據對人工神經網絡輸入－輸出模式進行訓練，即以訓練數據［（x1，y1），（x2，y2），…，（xn，yn）］逐級調整神經元權值和閾值，實現輸出期望值和實際網絡輸出值的均方差（yi－yout）2達到極小值.為提高網絡的收斂速度和泛化能力，筆者采用基于Levenberg－Marquardt法的BP網絡，即由輸出層向隱含層返回誤差值，并通過最小梯度下降法和高斯－牛頓法之間自適應調整優化隱藏層權重矩陣和輸出層權重矩陣.

筆者將TGA試驗所得數據作為訓練和測試神經網絡的基本數據，并應用3 755組數據構建神經網絡：① 輸入數據（樣品顆粒粒徑D；煅燒過程溫度Tcal；煅燒持續時間tcal；煅燒氣氛中CO2體積分數φ（CO2）；碳酸化持續時間tcar，min；循環次數n；上一次循環結束時碳酸化轉化率 Xcar，（n－1）；② 輸出數據（鈣基吸收劑碳酸化轉化率Xcar，n）.輸入數據取值范圍：D，38～180μm；Tcal，750～1 050 ℃；tcal，20～120min；φ（CO2），0～25%；tcar，0～20min；n，1～20；Xcar，n－1，0～1.

采用基于Levenberg－Marquardt法多層BP神經網絡，7個輸入層神經元（D、Tcal、tcal、tcar、φ（CO2）、n、Xcar，（n－1）），1個輸出神經元（Xcar（n，tcar））和中間一層或多層隱含層組織而成.原輸入數據和輸出數據經歸一化處理得到神經網絡輸入和輸出數據.隱含層傳遞函數采用正切Sigmoid函數，輸出層傳遞函數采用對數Sigmoid函數，以保證輸出數據在［0，1］之間.在3 755組試驗數據中，取2 843組作為神經網絡訓練數據，其余912組數據作為測試數據，均用于測試訓練后不同拓撲結構網絡的平均誤差和均方誤差.

表2為不同拓撲結構的神經網絡特性參數對比.驗證輸入數據無序輸入時計算誤差的重復性，確定最優拓撲結構為單一隱含層結構，隱含層神經元個數為46個.

3 試驗結果與分析

圖2為試驗數據與預測數據的對比.從圖2可知：多組不同輸入參數下神經網絡預測碳酸化轉化率與試驗數值呈正比關系，證明BP神經網絡可實現對鈣基吸收劑煅燒和碳酸化循環的準確模擬.圖3為粒徑48～62μm石灰石顆粒經850℃、20min、100%φ（N2）煅燒后第一次碳酸化循環的TGA試驗數據與BP神經網絡預測數值的對比.從圖3可知：利用BP神經網絡可以準確地反映煅燒反應參數對鈣基吸收劑碳酸化反應速率和轉化率的影響.因此，筆者設定煅燒條件為850℃，應用拓撲結構為7－46－1的優化BP神經網絡，以循環次數、吸收劑樣品物性（顆粒粒徑）和煅燒過程參數（煅燒溫度、煅燒氣氛及煅燒時間）作為輸入參量，模擬吸收劑碳酸化反應動力學特性以及其活性變化過程.

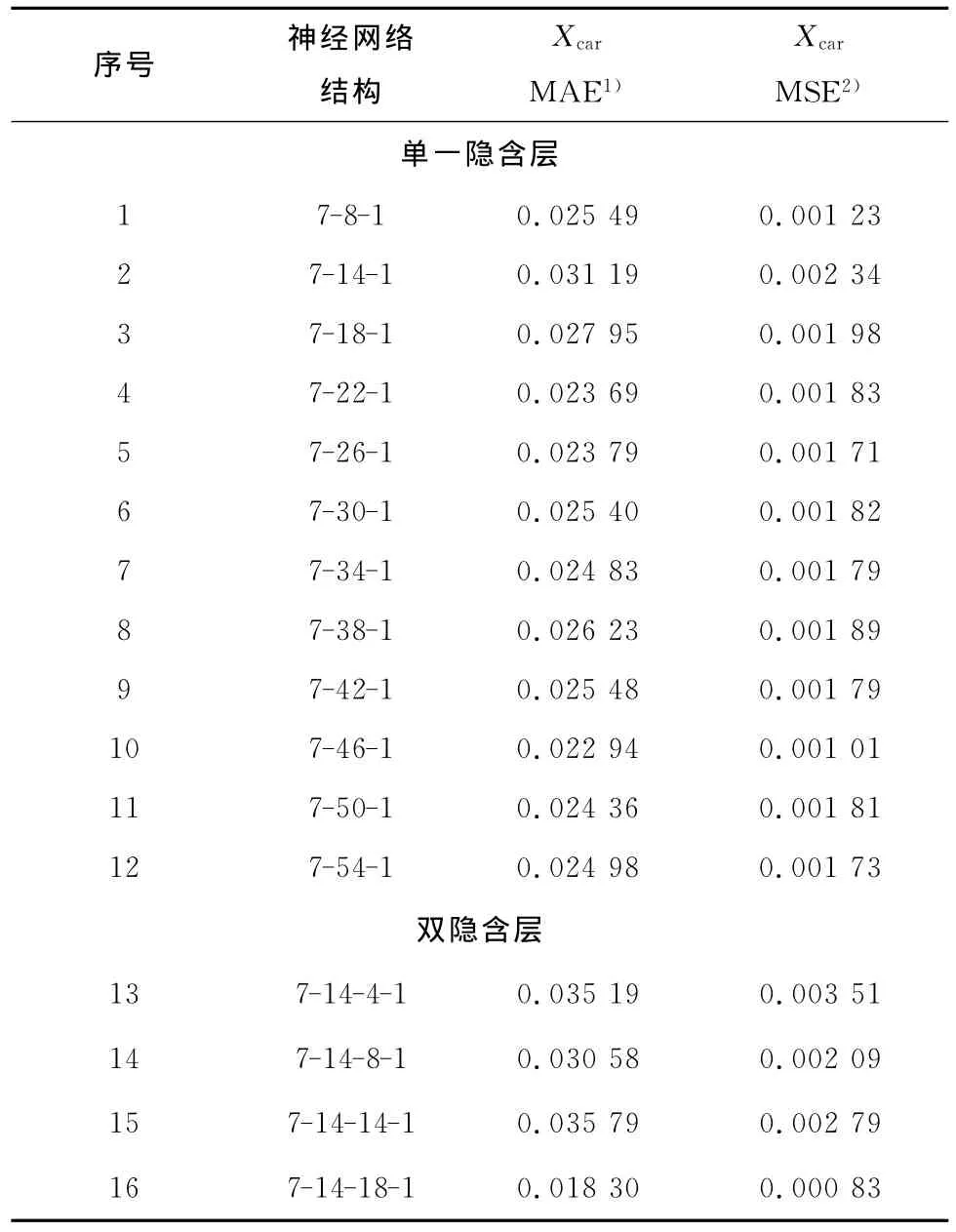
表2 不同拓撲結構的神經網絡特性參數對比Tab.2 Evaluation of an artificial BP neural network–comparison between neural network answers and the TGA experimental data

圖2 試驗數據與預測數據的對比Fig.2 Comparison between experimental and simulated data

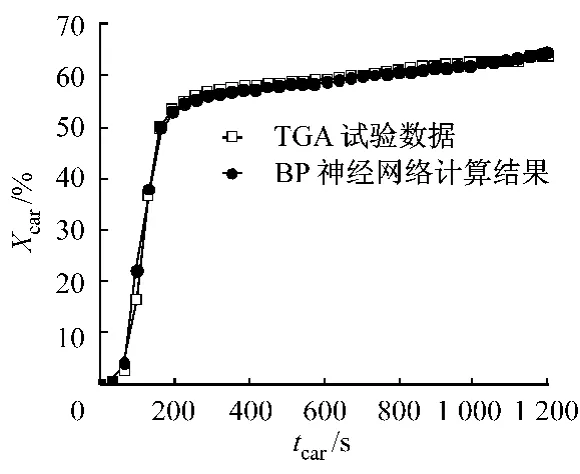
圖3 石灰石碳酸化試驗數據與預測數據對比Fig.3 Comparison of limestone carbonization between experimental and simulated data

粒徑為48～62μm石灰石顆粒經850℃、20 min、100%φ（N2），經20次煅燒和碳酸化循環后，其樣品顆粒的活性衰減曲線見圖4.從圖4可看到：TGA試驗數據與BP神經網絡計算數據基本吻合，說明BP神經網絡算法可以直觀反映CO2循環次數與吸收劑顆粒活性的關系.

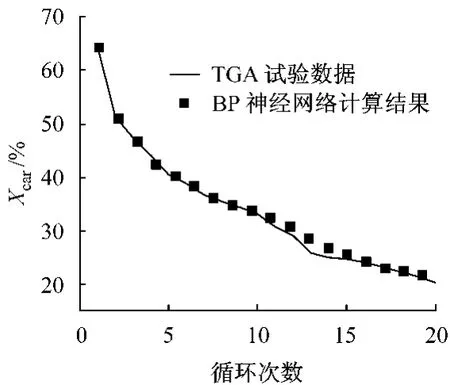
圖4 石灰石樣品顆粒的活性衰減曲線Fig.4 Comparison of limestone activity between TGA and BP network data

3.1 循環次數

鈣基吸收劑碳酸化過程包括快速化學反應和緩慢擴散反應兩個階段，兩個反應階段之間不存在過渡階段.當化學反應控制區域的碳酸化轉化率達到一定值時，立即進入擴散反應階段.隨著循環次數的增加，碳酸化反應過程曲線形態不發生變化，但是化學反應階段的碳酸化轉化率明顯降低，最終導致CO2吸收效率的降低［10－13］.

設定煅燒反應條件（Tcal為850℃、tcal為20min、100%φ（N2）），模擬顆粒48～62μm石灰石樣品經過20次循環，其CO2吸收過程即Xcar（n，tcar）曲線.圖5為BP神經網絡預測循環次數對吸收劑活性的影響.從圖5可以看出：石灰石樣品經歷多次循環碳酸化反應的曲線形狀極為相似，但是碳酸化轉化率明顯降低，當循環次數從1增加到5時，最終碳酸化轉化率由64.42%下降至40.15%，其中91.09%的減少量是由化學反應階段吸收效率降低造成的.循環次數的增加造成顆粒孔隙結構的變化，1次煅燒后鈣基吸收劑顆粒的孔隙分布集中于85～100nm的小孔，隨著碳酸化反應的進行，顆粒孔隙分布趨向于大孔，有效反應的比表面顯著降低，導致CO2吸收效率降低.當循環反應次數增加到15次時，最終碳酸化轉化率降低為24.06%；當循環反應次數增加到20次時，吸收劑顆粒僅能吸收20.81%的CO2，即隨著循環次數的進一步增加，碳酸轉化率進一步降低，但其衰減趨勢趨于平緩.

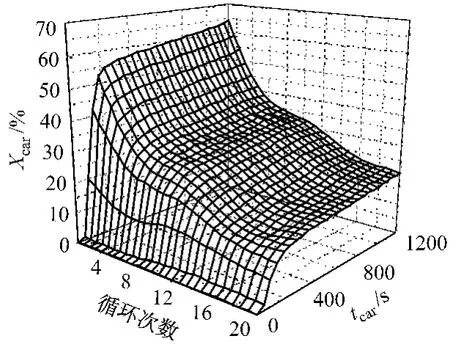
圖5 BP神經網絡預測循環次數對吸收劑活性的影響Fig.5 Influence of cyclic number on sorbent activity by BP neural network simulation

3.2 吸收劑顆粒粒徑

為研究顆粒粒徑對鈣基吸收劑碳酸化過程的影響，筆者在設定煅燒反應條件下（Tcal為850℃、tcal為20min、100%φ（N2）），將樣品劃分為4個粒徑區間：38～48μm、48～62μm、62～80μm和80～180 μm，模擬 CO2吸收過程，即Xcar（tcar）以及 Xcar（n）.圖6為BP神經網絡預測粒徑對吸收劑活性的影響.從圖6可知：第1次循環，顆粒粒徑不是影響CO2吸收效率的重要因素，不同的顆粒粒徑獲得比較接近的轉化率；但是粒徑為48～62μm的顆粒樣品化學反應階段較快速.樣品經歷5次循環后，粒徑為38～48μm顆粒的活性衰減曲線斜率略大于其他3組樣品.當循環次數增加到15次時，由于顆粒粒徑不同引起的碳酸化反應速率差異基本消失，而且粒徑為48～62μm、62～80μm和80～180μm樣品顆粒的碳酸化轉化率極為接近，分別為24.06%、24.28%和23.03%，但粒徑為38～48μm吸收劑顆粒的CO2吸收效率卻只有20.06%.因此，當顆粒粒徑小于48μm時，反應過程中顆粒的雜質相對含量起到了主導作用［14］.

3.3 煅燒反應參數

煅燒反應過程決定煅燒后吸收劑顆粒的孔隙結構、微顆粒結構和顆粒表面形貌，并直接影響到吸收劑的CO2吸收能力.圖7～圖10分別為BP神經網絡預測煅燒參數（煅燒氣氛、煅燒溫度、煅燒時間和高溫及長時間煅燒）對鈣基吸收劑活性的影響.

圖6 BP神經網絡預測粒徑對吸收劑活性的影響Fig.6 Influence of particle size distribution on sorbent activity by BP neural network simulation

圖7 BP神經網絡預測氣氛對吸收劑活性影響Fig.7 Influence of calcination atmosphere on sorbent activity by BP neural network simulation

圖8 BP神經網絡預測煅燒溫度對鈣基吸收劑活性的影響Fig.8 Influence of calcination temperature on sorbent activity by BP neural network simulation

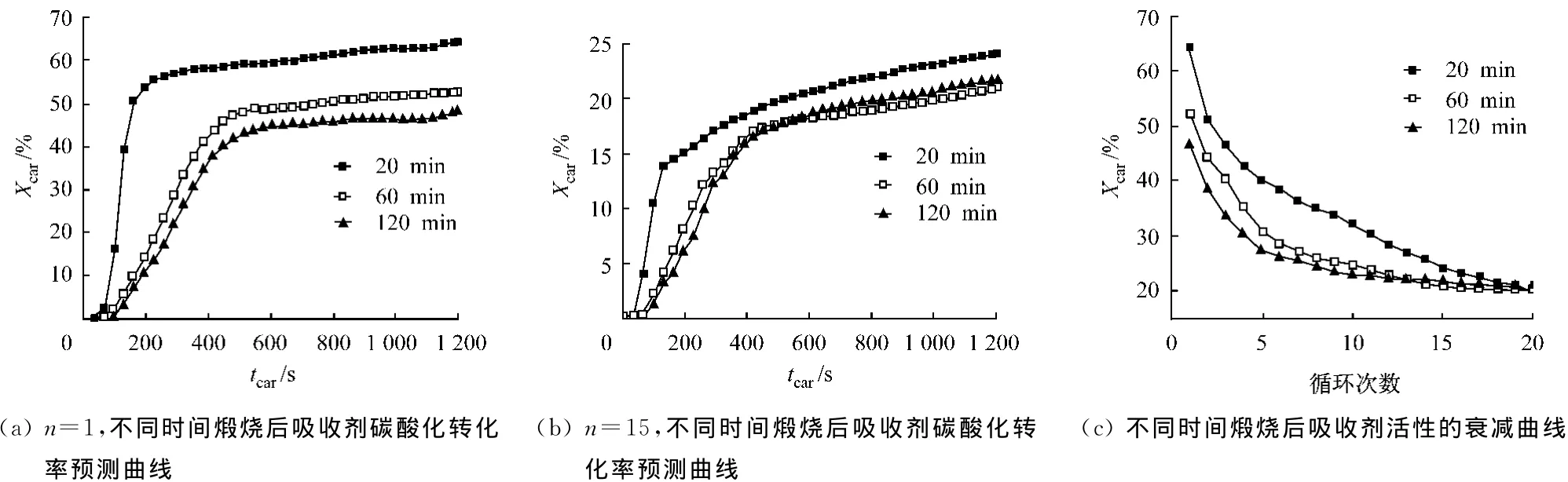
圖9 BP神經網絡預測煅燒持續時間對鈣基吸收劑活性的影響Fig.9 Influence of calcination duration on sorbent activity by BP neural network simulation

從圖7～圖10可知：吸收劑顆粒的表面CO2分壓力增大導致顆粒內部孔隙CO2擴散阻力增加，一定程度上促進顆粒內部大孔結構的形成，使顆粒熱解后比表面積降低，從而限制了顆粒對CO2的吸收；設定煅燒溫度為850℃、煅燒時間為20min和φ（CO2）由0%增加到25%時，神經網絡預測粒徑為48～62μm的樣品第一次碳酸化轉化率由63.93%下降為59.12%，而且隨著φ（CO2）的增加，鈣基吸收劑碳酸化反應的化學動力學階段的反應速率減小.在不同φ（CO2）下得到的吸收劑活性衰減曲線形態相似，基本遵循CO2加速活性衰減的規律.

圖10 預測高溫和長時間煅燒對鈣基吸收劑活性的影響Fig.10 Influence of both high calcination temperature and long duration on sorbent activity by BP neural network simulation

設定粒徑為48～62μm的石灰石樣品，煅燒溫度分別為750℃、850℃、950℃和1 050℃，在100%φ（N2）條件下煅燒20min，計算結果如圖8顯示：吸收劑顆粒經歷一次煅燒后，對應不同的煅燒溫度，其碳酸化轉化率和碳酸化反應速率均存在明顯差異.煅燒過程必定伴隨著顆粒的燒結，煅燒反應速率與燒結反應速率均隨著溫度的上升而增大，但是燒結反應速率對溫度的變化更為敏感，導致吸收劑顆粒經過相同時間的高溫煅燒后燒結程度加重，煅燒溫度越高，其燒結程度越嚴重，煅燒后顆粒比表面積越小，其吸收CO2的量越小［15］.在第一次煅燒和碳酸化循環中，當煅燒溫度由850℃提高到950℃時，其碳酸化轉化率由64.42%降低到41.41%；當煅燒溫度進一步上升到1 050℃時，吸收劑顆粒只能吸收26.79%的CO2，且化學反應階段的反應時間在增加，依次為192s、288s和320s.而且，隨著循環次數的增加，顆粒燒結程度加劇，限制了吸收劑反應能力.但值得注意的是：當煅燒溫度等于或大于950℃時，吸收劑的活性衰減速率反而相對平緩，特別是在進行15次循環之后，其CO2的吸收效率逐漸趨向于21.00%.

設定石灰石樣品粒徑為48～62μm，在100%φ（N2）、850 ℃ 下 分 別 煅 燒 20min、60min 和 120 min，筆者模擬了加劇顆粒燒結的另一重要因素——煅燒持續時間的影響結果見圖9.隨著煅燒時間的延長，一定程度上加劇了顆粒燒結，導致顆粒表面微顆粒熔融，顆粒內部小孔隙聯結成大孔，造成顆粒孔容積和顆粒比表面積損失，進而對碳酸化反應產生消極影響［16］.同時，長時間煅燒使活性衰減曲線相對平緩，如煅燒時間設定為120min時，樣品顆粒經歷10次循環，其CO2的吸收效率由46.61%下降到23.05%；10次循環后，樣品的碳酸化轉化率保持在21%～22%.

高溫煅燒和長時間煅燒均對吸收劑活性衰減起到抑制作用，因此在研究和分析兩者同時作用情況下吸收劑顆粒的反應活性變化過程時，筆者模擬經歷1 050℃高溫、120min煅燒熱處理后樣品顆粒，進行850℃（100%φ（N2））和650℃（15%φ（CO2））CO2捕集循環，預測高溫和長時間煅燒對鈣基吸收劑活性的影響，模擬結果見圖10.經熱處理后，樣品的反應活性經過15次循環即趨于穩定（≈24.50%），而未經過熱處理的吸收劑樣品則呈現典型的活性衰減曲線，經15次循環后的碳酸化轉化率為24.06%.高溫煅燒或（及）長時間煅燒后，吸收劑顆粒在碳酸化循環初始階段，反應活性的衰減是由于顆粒燒結帶來的孔隙比表面積以及孔容積的損失造成的，但隨著循環繼續進行，燒結理論和顆粒孔隙模型無法解釋這種反應活性保持的現象.因此，Monovic等提出了顆粒骨骼結構理論（顆粒由內部未反應硬質骨骼結構和外部軟質骨骼結構構成）解釋吸收劑顆粒活性衰減以及活性保持等現象［17］.

4 結 論

（1）BP神經網絡可以直觀、準確地描述各種非線性影響參數作用的復雜多相化學反應過程，結合TGA試驗數據與BP神經網絡模擬數據可減少試驗次數，并且可為模擬鈣基吸收劑煅燒和碳酸化循環反應過程以及反應活性變化提供新的方式.

（2）基于TGA試驗數據，訓練和測試Levenberg－Marquardt法優化的BP神經網絡，采用隱含層神經元為46個的單一隱含層神經網絡為最優拓撲結構.

（3）與傳統的回歸微分方程組模型比較，BP神經網絡算法在未曾簡化化學反應條件或忽略反應過程中傳質作用和固態遷移影響的前提下，可以直觀地反映影響參數對計算結果的作用，因此BP神經網絡可以準確地描述鈣基吸收劑碳酸化循環反應的特性.

［1］李英杰，趙長遂.基于鈣基吸收劑的循環煅燒／碳酸化反應吸收CO2的試驗研究［J］.動力工程，2008，28（1）：117－121.LI Yingjie，ZHAO Changsui.Experimental study based on calcium－based absorbent cyclic reaction （CCR）for CO2－capture［J］.Journal of Power Engineering，2008，28（1）：117－121.

［2］AUDUS H，FREUND P.The costs and benefits of mitigation：a full－fuel－cycle examination of technologies for reduction greenhouse gas emmisions［J］.Energy Conversion Management，1997，38（S）：S595－S600.

［3］ABANADES J C.The maximum capture efficiency of CO2using a carbonation／calcination cycle of CaO／Ca－CO3［J］.Chemical Engineering Journal，2002，90（3）：303－306.

［4］尚建宇，宋春常，王春波，等.石灰石煅燒及其產物碳酸化特性的試驗研究［J］.動力工程學報，2010，30（1）：47－51.SHANG Jianyu，SONG Chunchang，WANG Chunbo，et al.Experimental study on limestone calcination and CaO carbonation characteristics［J］.Journal of Chinese Society of Power Engineering，2010，30（1）：47－51.

［5］ALVERZ D，ABANADES J C.Determination of the critical product layer thickness in the reaction of CaO with CO2［J］.Industrial ＆Chemical Research，2005，44（15）：5608－5615.

［6］ERIC B，GONTRAND L，CORNELIUS S，et al.The decrease of carbonation efficiency of CaO along calcination－carbonation cycles：experiments and modeling［J］.Chemical Engineering Science，2009，64（9）：2136－2146.

［7］PARISI D R，LABORDE M A.Modeling steadystate heterogeneous gas－solid reactors using feedforward neural networks［J］.Comp Chem Eng，2001，25（9／10）：241－250.

［8］ABBAS T，AWAIS M M，Lockwood F C.An artificial intelligence treatment of devolatilization for pulverized coal and biomass in co－fired flames［J］.Com－bustion Flame，2003，132（3）：305－318.

［9］汪洋，余定華，孫鵬，等.基于神經網絡的乳酸脫水制丙烯酸仿真模擬［J］.化工學報，2009，60（1）：84－88.WANG Yang，YU Dinghua，SUN Peng，et al.Simulation of preparation of acrylic acid from lattice acid dehydration based on BP neural network［J］.CIESC Journal，2009，60（1）：84－88.

［10］GRASA G S，ABANADES J C.CO2capacity of CaO in long series of carbonation／calciantion cycles［J］.Ind Eng Chem Res，2006，45（26）：8846－8851.

［11］FENNEL P S，PACCINAI R，DENNIS J S，et al.The effect of repeated cycles of calciantion and carbonation on a variety of different limestones，as measured in a hot fluidized bed of sand［J］.Energy ＆Fuel，2007，21（4）：2072－2081.

［12］GRASA G S，ABANADES J C，ALONSO M，et al.Reactivity of highly cycled particles of CaO in a carbonation／calcination loop［J］.Chemical Engineering Journal，2008，137（3）：561－567.

［13］MANOVIC V，ANTHONY E J.Parametric study on CO2capacitu of CaO－based sorbents in looing cycles［J］.Energy ＆Fuel，2008，22（3）：1851－1857.

［14］MANOVIC V，AATHONY E J.Steam reactivation of spent CaO－based sorbent for multiple CO2capture cycles［J］.Environ Sci Technol，2007，41（4）：1420－1425.

［15］STANMORE B R，GILOT P.Review－calcination and carbonation of limestone during thermal cycling for CO2sequestration［J］.Fuel Process Technol，2005，86（16）：1707－1743.

［16］AGNEW J，HAMPARTSOUMIAN E，JONES J M，et al.The simultaneous calcination and sintering of calcium based sorbent under a combustion atmosphere［J］.Fuel，2000，79（12）：1515－1523.

［17］MANOVIC V，ANTHONY E J.Thermal activation of CaO－based sorbent and self－reactivation during CO2capture looping cycles［J］.Environ Sci Technol，2008，42（11）：4170－4174.