格網劃分的雙策略跟蹤多邊形裁剪算法

汪榮峰， 廖學軍

（裝備學院航天指揮系，北京 101416）

1 相關研究

不要求裁剪多邊形為矩形或凸多邊形的裁剪算法主要有3類：第1類是建立在比較完備的數學形式之上的算法，如Rivero等[1]和Peng等[2]提出的算法，其優點是理論基礎完備，無需考慮特殊情況、魯棒性好，缺點是算法較為復雜且效率提升困難；第2類算法將交點分割后邊分類跟蹤形成子區域，通過子區域運算實現多邊形布爾運算，如Schutte[3]、Leonov-Nikitin[4]、朱雅音[5]等算法；第3類在Weiler算法[6]基礎上得到，將交點分類為進點和出點，進行跟蹤得到輸出多邊形，如 Vatti[7]、Greiner-Hormann[8]、劉勇奎[9]等算法，其原理簡單、易于實現，效率較高，本文提出算法也屬于此類。

第3類算法的研究集中在3個方面：

1）數據結構設計。Weiler 算法使用樹形數據結構，Vatti 算法和 Greiner-Hormann 算法使用雙線性鏈表數據結構，劉勇奎算法采用單鏈表數據結構。

2）特殊情況處理。需處理的特殊情況是交于頂點和邊重合等情況。文獻[7]和文獻[9]采用對頂點進行微小移動的方法，這對于屏幕繪制等有效，但需精確結果時不適用；鮑虎軍[10]根據多邊形邊界內法向來對交點進行完備分類；劉勇奎[11]將特殊情況分解成各種子情況分別進行處理，通過在鏈表上增加或減少交點來保持進點出點交替出現。

3）求交效率優化。裁剪算法中最為耗時的是求交點，在不進行任何優化的情況下其時間復雜度為 O(nm)。文獻[11]提出了斜率法來優化兩邊之間的求交運算，對每個點需要執行一次除法；文獻[10]提出了應用錯切變換處理邊求交問題，進一步減少了求交所需運算量；在針對兩條邊的求交運算上，這兩種方法基本已經達到最優，但是就多邊形裁剪而言，并沒有減少總的求交次數。文獻[8]在邊求交中應用了線段包圍盒等技術快速排除不需求交的情況，但是其求交時間仍占全部耗時的 80%以上。文獻[3]提出了應用空間剖分技術以使得每條邊不必與所有其它邊求交的設想，但并未就該技術展開深入研究。姚輝學等[12]提出將兩個多邊形的公共包圍盒范圍劃分為格網，然后將邊歸屬于相應網格中，在邊求交時只計算與所處理邊位于同一網格內的邊；但是該文獻在處理邊與網格關系時采用辦法是判斷邊與所有網格的關系，同時該方法會導致一組邊重復計算交點的問題，得出的結論是一個網格內邊數在 80 ～100之間時效率最佳，這種程度的優化非常有限。

2 新算法的原理

以往算法一般將交點劃分為進點和出點兩類，對于交于頂點和邊重合的情況，將其歸類為進點或出點。與上述思路不同的是，本文將交點劃分為普通交點與頂交點兩類，普通交點和頂交點的定義如圖1所示，多邊形S和C相交，普通交點為I1、I2和I3，頂交點為C3、C4、S4；在進行跟蹤獲得輸出多邊形的時候，針對這兩類交點的特點，構造了不同的跟蹤策略，以此來確保輸出結果的正確。跟蹤策略及過程將在第5節討論。

在效率優化上，邊與邊求交本身已經基本沒有優化空間，更重要的是如何讓邊只與可能有交的邊求交。本文的方法是：將頂點數目多的多邊形的邊劃分到空間網格中，而在邊劃分到網格的過程中，采用了類似于直線段掃描轉換Bresenham算法的技術，使得劃分過程的效率達到最優；而求交點時則以另一個多邊形的邊來與網格中多邊形的邊求交，并通過簡單的賦值和比較避免了重復求交問題。第4節將討論邊求交過程。

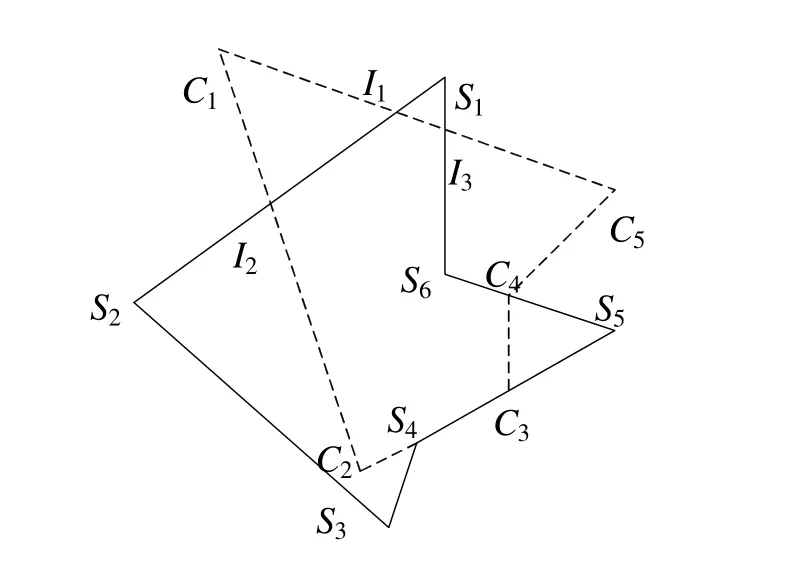
圖1 普通交點和頂交點的定義

3 算法采用的數據結構

劉勇奎算法針對頂點和交點定義了不同的數據結構，雖然頂點的定義節省了1個指針，但是在遍歷鏈表的時候將不得不額外區分頂點和交點；Greiner-Hormann算法中采用相同的數據結構表示頂點和交點，用1個boolean數據作為交點標志，在遍歷節點時只需判斷標志即可。本文以相同的數據結構表示頂點、普通交點和頂交點，鏈表結點定義為（其中 coordinates 表示坐標類型；vertexPtr表示指針）：

vertex={x,y: coordinates;

其中tag域表示節點的類型，值為0表示頂點，值1表示普通交點，值2表示頂交點；alpha域表示以參數形式表示的交點坐標，范圍在0到1之間，當同一邊上有多個交點時，利用該參數進行排序；cnt域用于避免重復求交；next域表示指向下一結點的指針；對于交點，other域指向另一鏈表對應交點。圖2給出了對圖1的兩個多邊形進行裁剪時形成的鏈表（結點內標出其 tag域的值）。

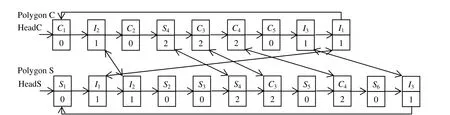
圖2 對圖1的多邊形進行裁剪時算法產生的鏈表數據結構

4 交點判斷與計算

網格劃分的目的是減少參與求交的邊數，如果網格劃分的效率足夠高且不同網格中的同一組邊不發生重復求交，則劃分越細則實際參與求交邊數越少。統計表明，本文算法中每個網格平均邊數在3 ～5個之間效率最優。根據多邊形包圍盒寬度、高度和多邊形頂點數，劃分為 Gx×Gy的網格，然后計算每個網格邊長Δ及其倒數δ。

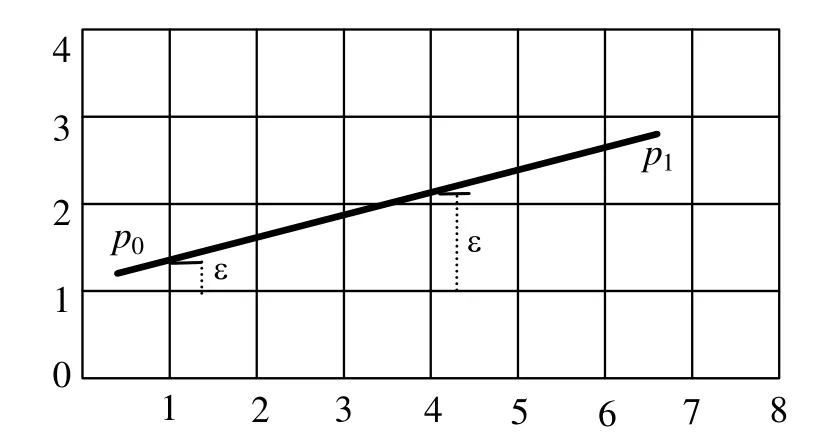
圖3 邊的網格劃分算法

文獻[12]采用對于每條邊逐個判斷網格是否與其相交，效率極低。構造了可以消除浮點除法運算的算法：邊沿起點網格前進到終點網格，每次在主方向前進一個網格，而構造誤差確定在另一個方向是否前進。定義誤差ε為線段與副方向網格線的交點與網格線的差，如圖3所示，對于垂直網格線1，其ε小于網格邊長Δ，在副方向不前進，邊經過網格(0,2)；對于垂直網格線 4，累計計算的ε大于Δ，副方向前進，邊經過網格(3,2)和(3,3)。問題歸結為如何計算ε初值以及遞推公式，設起點所在網格為(i,j)，邊起點到終點的差值為dx、dy，網格水平方向最小值為xmin，起點坐標為(x0,y0)，則初值和遞推公式為

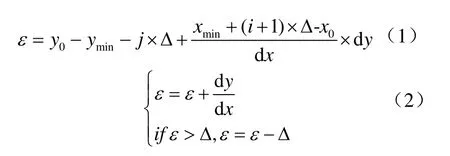
由于上式的作用是通過比較進行判斷，因此將初值、步進值和比較參考值同時乘以dx，消除浮點除法運算。以x方向為主方向，向右上方前進時的網格化算法見算法1。

算法 1邊v0v1的網格劃分

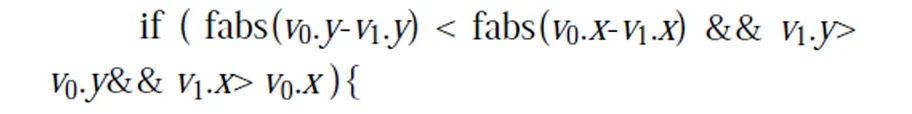
計算v0所在的網格并設置為當前網格;

算法1中，循環次數基本等于邊所經過的網格數，最大不會超過max{Gx,Gy}，大部分情況僅需處理很少的網格，既不需判斷多余網格，每個網格內運算量也非常小。

將邊數較多的多邊形進行網格劃分后，以另一個多邊形的邊與該邊所經過的每個網格內的邊求交，采用與算法1基本一致的方法確定邊經過的網格，然后求交，算法略。在數據結構中定義了cnt域，該值隨著求交的邊變化而增長，當網格內另一多邊形邊的cnt域值已經和求交邊的值相同，則表示兩者已經進行過求交，避免重復求交。

5 雙策略跟蹤得到輸出多邊形

針對交點和頂交點構造不同跟蹤策略，交替使用2個跟蹤策略，得到輸出多邊形。

遇到交點的跟蹤策略是直接由一個鏈表切換到另一個鏈表，見算法2，其中PS和PE是參數，分別表示跟蹤當前指針和跟蹤起點指針。

頂交點的下一結點有3種可能：頂點、交點和頂交點。如下一結點為頂點和交點，通過判斷該點與另一多邊形位置關系來決定是否進行鏈表切換；如下一結點為頂交點，則當前結點與下一結點所形成線段可在另一多邊形之內、邊界上或之外。根據當前結點與下一結點中點與另一多邊形位置關系來決定是否進行鏈表切換：如果中點在另一多邊形之內或邊界上，不切換鏈表，否則切換鏈表；根據下一結點類型選擇繼續采用哪個跟蹤策略。

以上算法根據交點類型交替、遞歸地調用2種跟蹤策略函數，跟蹤過程非常簡潔、直接，算法易于實現，但會帶來一定函數調用開銷。

6 算法效率分析與比較

算法包括3個主要部分：多邊形網格劃分、邊求交、跟蹤，設多邊形邊數分別為 m、n，下面分析平均情況下的時間復雜度。

多邊形網格劃分，每個多邊形邊所經過網格數不確定，與多邊形邊數、形態等都有關，測試中平均經過 2 ～5個網格，時間復雜度為O(max(m,n))；邊求交，由于網格劃分很細，邊只與其所經過網格的邊求交，平均情況下時間復雜度為O(min(m,n))；跟蹤，遍歷鏈表的時間復雜度為O(m+n+k×2)，其中k為交點個數。

選取了一些不同頂點數（N為2多邊形頂點數之和）的多邊形，測試了算法各個步驟的執行時間。新算法與參照算法都在VC6.0實現，時間測試使用高精度時間函數QueryPerformanceFrequency()，運行在主頻 3.0G的普通微機，測試結果如表1所示。

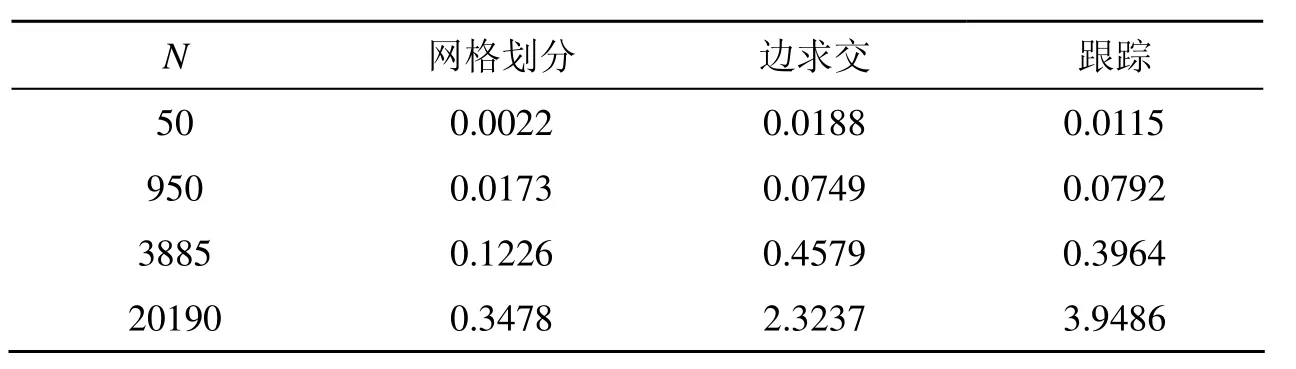
表1 算法3個主要步驟所需時間的比較(ms)

從表1中可以看出：① 網格劃分的效率非常高，在整個算法中所占的時間比例很小；② 求交所用時間與跟蹤所用時間在一個量級，這較之于一些傳統算法有了較大的改進。

將本文算法與 Vatti算法、Leonov算法和Schutte算法進行對比，比較結果如表2所示。新算法比Vatti算法、Leonov算法的效率高出1 ～2個數量級，Schutte算法效率很低，不具可比性。文獻[9]對劉勇奎算法、Vatti算法和Greiner-Hormann算法進行了比較，其中Greiner-Hormann算法耗時約為 Vatti算法的一半，劉勇奎算法耗時約為Vatti算法的三分之一。結合該比較結論可以看出，本文算法的效率也遠優于Greiner-Hormann算法和劉勇奎算法。在表2中，當多邊形點數較多時，Schutte算法無法正確執行，用“*”表示。

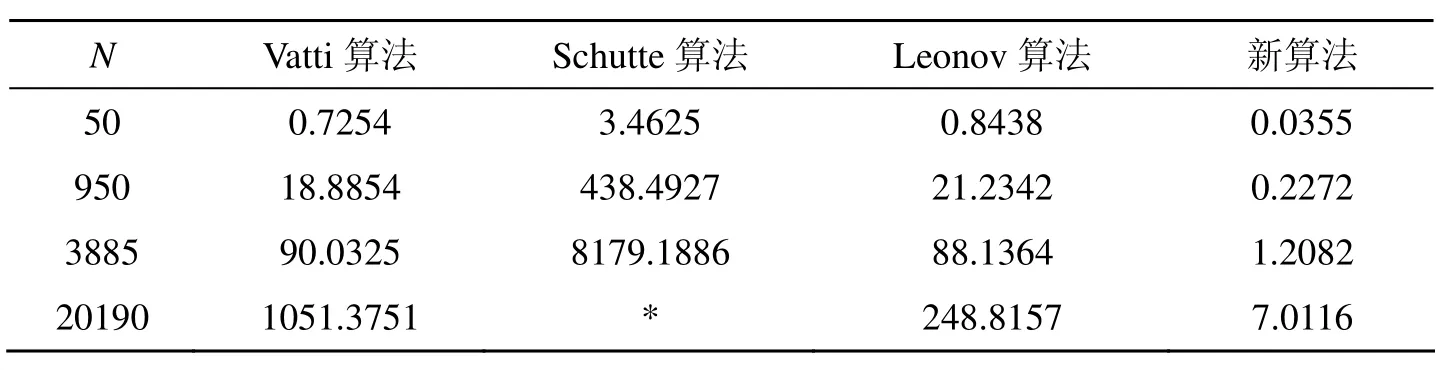
表2 新算法與Vatti算法、Schutte算法和Leonov算法運行時間的比較(ms)

7 結 束 語

網格劃分是計算機圖形學中的一項常用技術，文獻[12]實際也采用了類似技術，本文創新在于劃分過程中邊的處理方法以及避免重復求交的方法，顯著提升求交效率；同時本文提出了雙策略跟蹤的方法，在跟蹤環節解決算法的魯棒性，對于交點落在邊上、邊重合等各種情況都確保結果正確，這也有別于傳統算法。

在適用性方面，本文算法存在如下局限：算法主要適用于多邊形邊數較多的場合，當邊數少于 15條時，可以不進行網格劃分；對于多邊形的邊分布比較極端的情況，如過多的邊集中在一個網格內，算法的效率優勢并不明顯。

[1] Rivero M L ,Feito F R. Boolean operations on general planar polygons [J]. Computers and Graphics,2000,24(6): 881-898.

[2] Peng Y,Yong J H,Dong W M,et al. A new algorithm for boolean operations on general polygons [J].Computers and Graphics,2005,29(1): 57-70.

[3] Schutte K. An edge labeling approach to concave polygon clipping [EB/OL]. (2007-11-7) [2010-7-12]http://citeseerx.ist.psu.edu/viewdoc/summary? doi=10.1.1.23.6997

[4] Leonov M V,Nikitin A G. A closed set of algorithms for performing set operations on polygonal regions in the plane [EB/OL]. (2002-11-24)[2010-7-12] http://www.complex-a5.ru/polyboolean/downloads/polybool_eng.pdf

[5] 朱雅音,王化文,萬 豐,等. 確定兩個任意簡單多邊形交、并、差的算法[J]. 計算機研究與發展,2003,40(4): 576-583.

[6] Weiler K,Atherton P. Hidden surface removal using polygon area sorting [C]//Proceedings of the SIGGRAPH’77. New York: ACM Press,1977:214-222.

[7] Vatti B R. A generic solution to polygon clipping [J].Communications of the ACM,1992,35(1): 56-63.

[8] Greiner G,Hormann K. Efficient clipping of arbitrary polygons [J]. ACM Transactions on Graphics,1998,17(2): 71-83.

[9] 劉勇奎,高 云,黃有群. 一個有效的多邊形裁剪算法[J]. 軟件學報,2003,14(4): 845-856.

[10] 鮑虎軍,彭群生. 一個有效的多邊形裁剪算法[J].自動化學報,1995,22(6): 741-744.

[11] 劉勇奎,顏 葉,石教英. 一個有效的多邊形窗口的線裁剪算法[J]. 計算機學報,1999,22(11):1209-1214.

[12] 姚輝學,盧章平. 一種任意復雜程度二維多邊形的求交算法[J]. 工程圖學學報,2006,27(2): 127-131.