新型破甲殺傷雙用途子母彈對典型目標射擊效力仿真

陶海軍，吳曉云，仇 磊

(陸軍軍官學院，合肥 230031)

國產某火箭炮武器系統配備了新型破甲殺傷雙用途子母彈作為其主力彈種，該型子母彈射程遠、威力大，主要用于打擊戰役戰術縱深內的高價值目標。由于其造價十分昂貴，所以不論在平時還是在戰時，都不可能像普通火炮那樣大量發射炮彈用于檢驗射擊效力，所以要評估其射擊效力，只能采用預測或預估的方法。目前采用的解析法，如相當“榴彈”法、母彈(子彈)積分法等，這些方法都沒能較好地克服子母彈的“毀傷重疊”問題。而Monte-Carlo 法，具有隨機事件仿真的功能，它是以高容量和高速度的計算機為前提條件的，是一種計算機上的隨機實驗，即在計算機上的“打靶”。我們可以在計算機上對一個目標“發射”幾百枚至上千枚“火箭彈”，據其統計的“射擊”結果，就能具有很高的可信度及精度，用這樣的結果還可以檢驗或修正解析算法的結果和模型。

1 基本模型

仿真法建立的數學模型大多與解析法不同，但也有相似和借用之處，盡管2 種方法分析思路不同，但都根植于射擊的事理，因此有些模型，2 種方法都可使用。

1.1 目標仿真

目標仿真就是將目標的實際面積轉化為它的等效圓來處理。目標區系平面直角坐標系，以中心為目標位置(或面目標中心位置)，各目標在該坐標系中的描述方法為:

1)點目標。面積Ld× Lf，則先計算目標等效圓，半徑在坐標系xoy 中的方程:設點目標中心位于原點位置，有單個面目標也可按上式表示。其他目標如線狀目標也按點目標的描述方法，體現其形狀特點。

2)集群目標。集群目標是由若干個單位目標組成的。設某單位目標的中心位置為(xTj，zTj)，(j =1，2，…，M);其中M 為集群目標中的單位目標數，j 為單位目標序號，RTj為第j個單位目標的等效圓半徑，則各單位目標按下列方程描述。

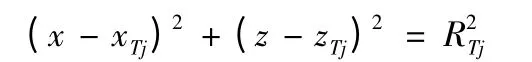
1.2 單發母彈(子彈散布中心)仿真

以遠程火箭炮單炮對目標的瞄準點作為母彈(子彈散布中心)的理想落點，再根據火箭彈CEP，即可仿真母彈(子彈散布中心)的實際落點。還可以根據射擊誤差分組情況，由諸元誤差的方差和散布誤差的方差分步來進行仿真。

1.3 子彈炸點(落點)仿真

子彈炸點(落點)的仿真，按照遠程火箭炮的特點，在單發母彈的平均拋撒子彈散布圓內均勻產生子彈的炸點(落點)。

1.4 毀傷判定及射擊效力統計

1.4.1 子彈命中判定

子彈命中目標分2 種情況［1］:一是子彈直接命中目標;二是子彈威力觸及目標。通過判斷子彈實際落點與目標中心之距離是否小于目標等效圓半徑來判斷子彈是否直接命中目標。通過判斷子彈落點與目標中心距離是否小于目標等效圓半徑與子彈威力半徑之和來判斷子彈是否坐標毀傷目標。

1.4.2 目標毀傷判定及射擊效力統計

目標毀傷的判定和解析法相同。比如:第j 個單位目標的等效圓半徑為RTj，目標毀傷平均命中彈數ω=1，目標中心點的位置為(xTi，zTi)，子彈落點(炸點)的位置為(xi，zi)，只要滿足條件:

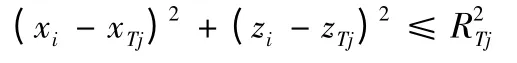
子彈就會命中且毀傷目標。如ω≠1，統計命中目標的子彈數，只要大于ω 則目標被毀傷。

或按照以下方法處理:在求得一發母彈所有子彈的落點坐標以后，即可依次判斷n 發子彈是否落入第j 個單位目標等效圓內。若落入目標等效圓內，則子彈命中目標。若毀傷目標所需的平均命中彈數ω=2，故可產生一個0 ～1 的均勻隨機數λ。當λ 屬于0 ～1 的一個長為a =1/2 的區間內時，則認為目標被毀傷。不失為一般情況，取該區間為［0.3，0.8］，此時，RN(j)=1;否則RN(j)=0。

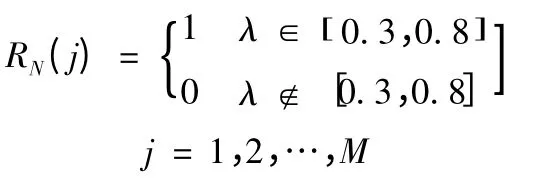
依據目標毀傷準則，根據以上仿真結果，判定目標毀傷情況，可求得一次齊射對目標的毀傷的數學期望［2-3］:

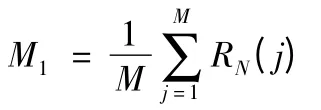
重復以上步驟，進行N0次模擬，得到模擬結果M1，M2，…，MN0

則毀傷比的數學期望:

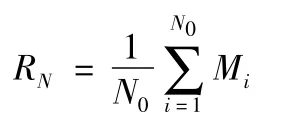
以此作為計算射擊效力的指標。

2 初始計算條件

2.1 計算條件

遠程火箭炮單炮對幾種典型目標射擊，假定一次齊射發射破甲殺傷雙用途子母彈12 發，火箭炮每發母彈拋撒子彈數為600 枚，拋撒子彈散布圓平均半徑為120 m，火箭炮決定諸元誤差為0.3%D，散布誤差為1/300D (D 為射距離)。

2.2 幾種典型目標

幅員為500 m×500 m 的坦克連集結地域，坦克數量為10 輛，坦克在集結地域內均勻分布。瞄準位置為集結地域中央。多管火箭炮(MLRS)排陣地，配置數量為3 門，炮與炮間隔為250 m，分別呈三角形、一線配置，瞄準位置陣地中央。“帕拉丁”自行火炮排陣地，配置數量4 門，每2 門為一組，炮與炮間隔100 m，2 組之間間隔300 m，呈一線配置，瞄準位置為陣地中央。坦克連行進縱隊，坦克數量10 輛，間距100 m，瞄準位置縱隊中央。

3 仿真的實現

3.1 隨機數的產生

隨機數的產生是仿真計算的關鍵，而具有良好統計特性的隨機數是獲得可靠的仿真結論的主要保證。下面是2 類隨機數的產生方法［4-5］。

3.1.1 均勻分布隨機數的產生

下面使用的U(0，1)隨機數采用素數模乘線性同余發生器PMMLCG 產生。其方法如下:設有一個整數序列Z1，Z2，…，Zn，定義

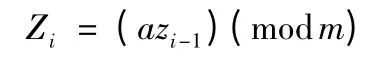
如果a 和m 滿足條件:

1)m 為小于2b的最大素數。其中b 為計算機除符號位以外的字長。

2)a 為模m 的一個質元素。即在al-1 可以被m 整除的情況下，最小的整數為l=m-1。

則可以證明PMMLCG 具有滿周期P=m。

對于32 位計算機，去掉符號位，則b=31，

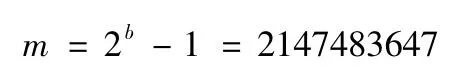
經過驗證，性能比較好的PMMLCG 有:

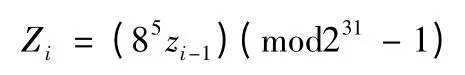
對上式進行歸一化處理:

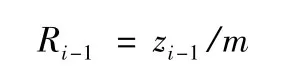
即可得到服從U(0，1)分布的隨機數序列{Ri}。

3.1.2 正態分布隨機數的產生

設r1和r2為2 個獨立的均勻分布隨機數，且服從U(0，1)作變換:

則η1和η2是2 個獨立的N(0，1)隨機數。由此可見，正態分布隨機數的產生可歸結為均勻分布隨機數的產生。

3.2 子彈落點坐標的仿真實現

由射擊誤差的數學模型可知，第i 個子彈落點的坐標:

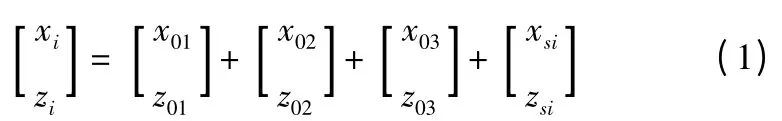
以σmx和σmz來產生正態隨機數x0m，z0m(m =1，2，3)，并將子彈對落點中心的偏差作為xsi和zsi(i=1，2，…，600)。

若假定子母彈射擊指向點與目標中心重合，則可求得一發母彈中所有子彈相對于目標中心的坐標:

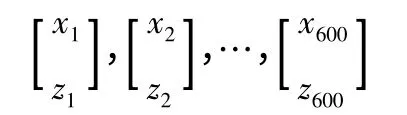
共有600 個坐標。遠程火箭炮單炮一次齊射時，則應產生12 ×600 =7 200 個子彈坐標，此為一次仿真模擬的結果。

3.3 結果與分析

3.3.1 仿真結果

根據以上基本思路及情況設置，編程進行仿真(仿真模擬次數為2 000)的結果見表1。

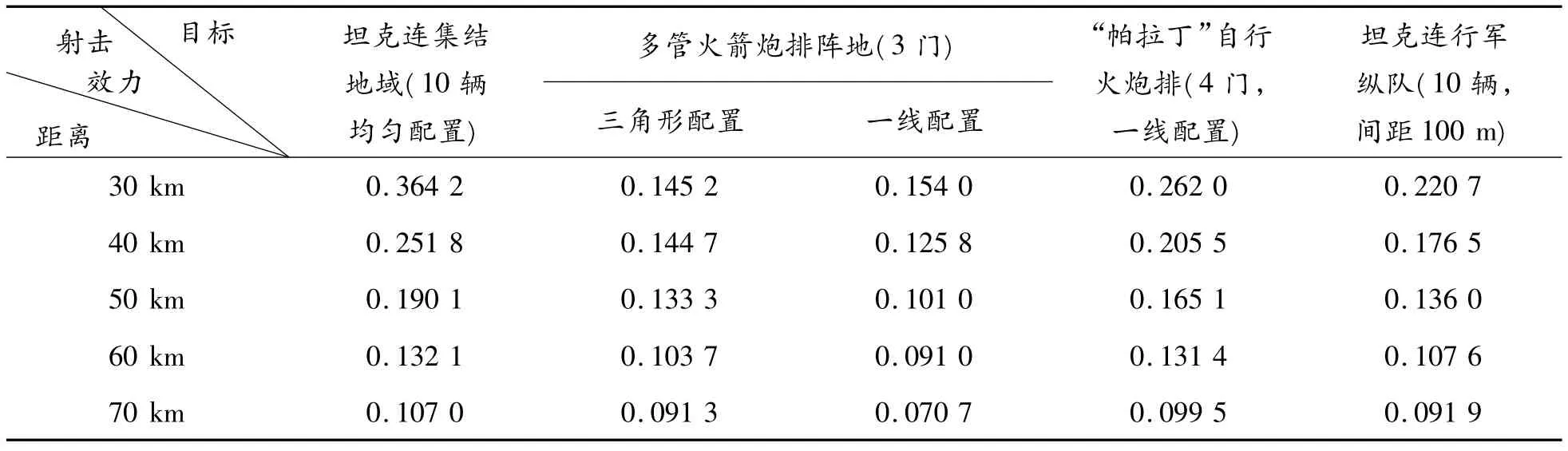
表1 單炮發射破甲殺傷雙用途子母彈對典型目標射擊，一次齊射的射擊效力仿真結果

3.3.2 結論

根據計算機仿真模擬2 000 次的結果看，遠程火箭炮單炮在常射距離上對上述4 種典型目標射擊，一次齊射12 發破甲殺傷雙用途子母彈，即可達到15%左右的毀傷。

按照文中的仿真算法，用兩門遠程火箭炮射擊，兩炮瞄準位置之間間隔為120 m(或選取適當位置)，各進行一次齊射，通過仿真試驗，集結地域的坦克連、坦克連行進縱隊和“帕拉丁”自行火炮都將有25%以上被毀傷。若用排(3 門炮)射擊，經仿真計算，射擊距離為50 km，對集結坦克連可達到35% 左右的毀傷;對MLRS 多管火箭炮排的毀傷在30%以上;對“帕拉丁”自行炮排射擊可達到約40%的毀傷。由此可見，對上述幾種典型目標射擊時，參加射擊的兵力應根據戰術需要或作戰任務，可選定1 ～2 門或排射擊，在火力分配上應采取單炮分段射擊的方式，以獲得最佳射擊效果。

［1］張廷良，陳立新.地地彈道式戰術導彈效能分析［M］.北京:國防工業出版社，2001.

［2］靳樹昌. 現代炮兵射擊學［M］. 北京: 軍事科學出版社，1999.

［3］許梅生.炮兵射擊基本理論分析［M］.北京:兵器工業出版社，2004.

［4］靳樹昌.遠程火箭炮射擊理論研究［M］.北京:海潮出版社，2005.

［5］程云門. 評定射擊效率原理［M］. 北京: 解放軍出版社，1986.