PSS2A低頻段振蕩抑制效果驗證方法
余 振,郭春平,安 寧
(國電南瑞科技股份有限公司,江蘇南京,210061)
隨著全國各省、各地區電網的快速發展以及電網之間的聯網輸電,電力系統低頻振蕩的現象時有發生,特別是西電東輸工程以及三峽機組的建成發電,低頻振蕩的頻率有向0.15 Hz或更低發展的趨勢。因此,要求電網中有更多的中、大型機組投入電力系統穩定器(PSS)[1]。2010年大唐某電廠曾經發生了0.8 Hz的低頻振蕩,事后檢查發現,當時電網側和電廠側正常,沒有故障情況發生,后來在該低頻值下對該機組采用負載階躍試驗進行再次驗證,PSS2A所提供的阻尼是正的。針對該事故現象,有必要對PSS2A在系統1 Hz以下的低頻振蕩抑制驗證方法進行討論分析。
1 PSS2A原理
為了防止在發電機原動機出力變化速率較快時,PSS輸出過大而導致發電機無功變化超出允許的范圍,目前PSS通常采用加速功率型PSS2A模型,如圖1所示。
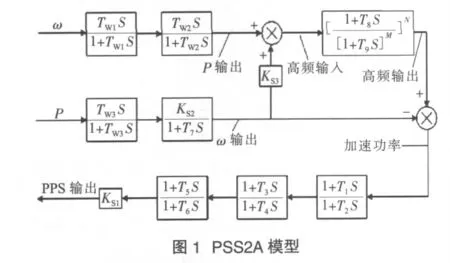
圖中,ω為發電機軸的旋轉角速度;P為發電機的電磁功率;高頻輸入為機械功率;TW1~TW4為隔直時間常數;KS1為PSS放大系數;KS2,KS3為電功率通道系數;T1~T6為超前及滯后時間常數;T7為慣性時間常數;T8,T9為高階濾波器的時間常數;M,N為高階濾波器的階數。
根據發電機轉子運動方程:
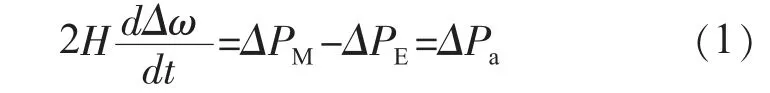
式中:H為發電機轉動慣量;PM為機械功率;PE為電氣功率;Pa為加速功率;ω為發電機軸的旋轉角速度。寫成頻域的形式:
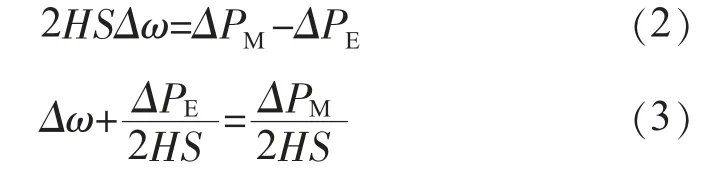
角速度信號和電磁功率信號的積分組合形成機械功率積分信號。該信號與電磁功率積分信號的差即為加速功率積分信號。
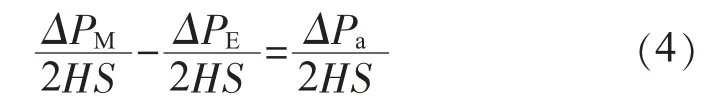
以加速功率積分信號作為輸入的PSS理論上沒有反調現象。當進行機械功率調節時,電磁功率跟隨機械功率變化,因此加速功率積分信號很小,PSS基本不動作;當系統擾動引起電磁功率變化時,機械功率變化較小,加速功率積分信號基本上等于負的電磁功率積分信號,PSS發揮作用抑制功率振蕩[2,3]。
2 高階濾波環節對振蕩的影響
圖1模型中有2個輸入量,分別是電磁功率P和轉速ω,其中P可以通過機端電壓和機端電流直接計算出來,一般都很準確;而ω的直接測量較為困難,需要通過軟件進行計算,計算過程中通常要用到交軸電抗,而交軸電抗事實上為一個變值,很難獲得,因此ω輸入可能在部分頻段計算不太準確,則經過兩階隔直環節(TW1,TW2)后,再與P通道輸出相加后得出的機械功率積分信號就可能不準確。
圖1中的T8,T9構成的高階濾波環節,其目的是濾除ω通道產生的噪聲,其理想特性應該是在低頻段增益為1,相角為0,而在高頻段增益為0,但實際中不可能,只能取得近似的效果,給PSS2A在過渡區帶來了一些負面影響,所以T8,T9參數的設計影響PSS在過渡區頻帶內的作用效果。T8=0.2 s,T9=0.1 s,M=5,N=1對抑制軸系扭振有好處;T8=0.6 s,T9=0.12 s,M=5,N=1對減少反調有好處。仿真后該環節的相頻幅頻特性如圖2和圖3所示。
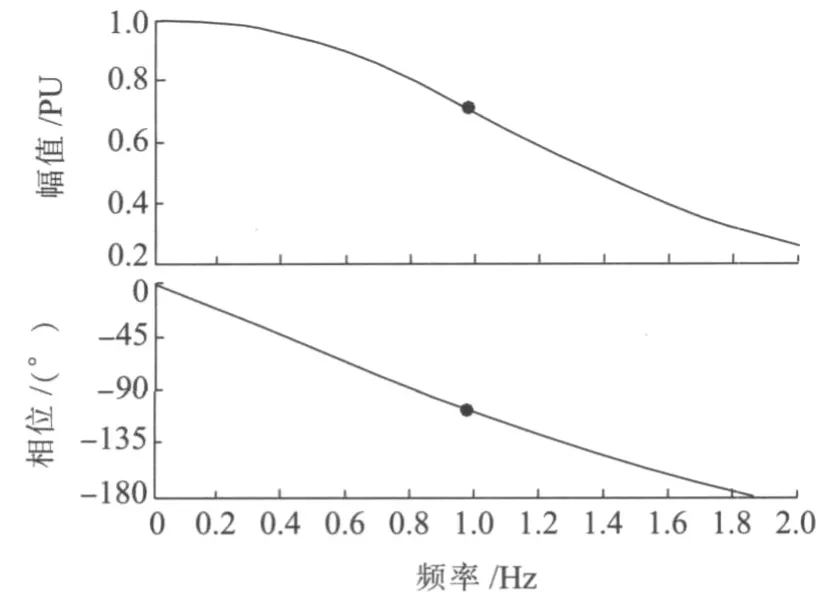
圖2 T8=0.2 s,T9=0.1 s高階濾波環節伯德圖
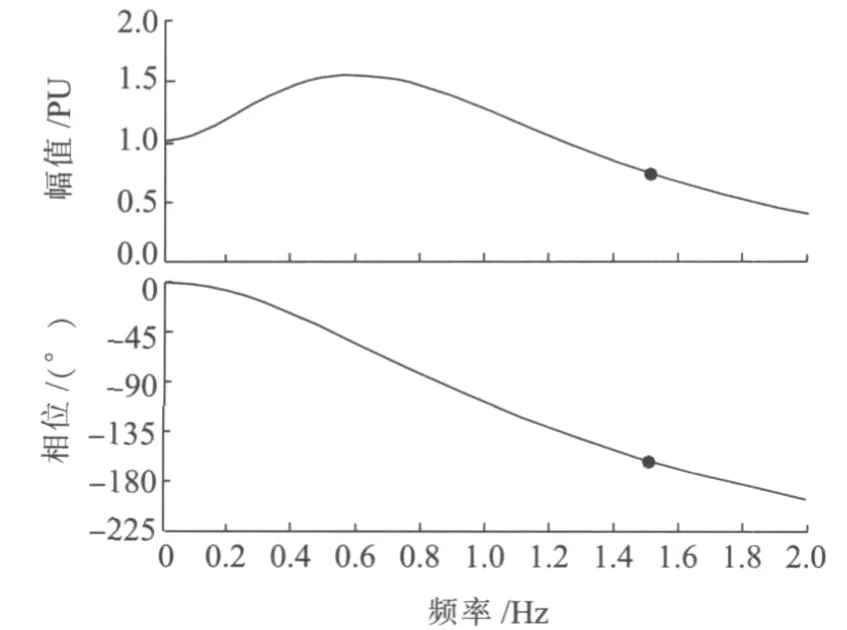
圖3 T8=0.6 s,T9=0.12 s高階濾波環節伯德圖
圖2中T8=0.2 s,T9=0.1 s時截止頻率為0.987 Hz,圖3中T8=0.6 s,T9=0.12 s時截止頻率為1.53 Hz,因此對于較高頻率的波動通過該環節后被大幅度衰減,這樣對P通道輸出和ω通道輸出的相加,在高頻段就有可能被濾掉,使高階濾波環節的輸出值很小,此時PSS2A模型就近似于PSS1A模型。因此在PSS的超前滯后環節(T1~T6)補償準確的前提下,對于1 Hz以下的振蕩,P通道和ω通道二者的相加會有較大的輸出,如果機械功率積分信號的計算不準確,會導致加速功率的計算不正確,那么PSS2A的抑制效果低頻段與高頻段相比較會較差,可能達不到PSS試驗導則所要求的阻尼比。而對于1 Hz以上的振蕩,即使機械功率積分信號的計算不準確,由于高頻濾波的作用,會使加速功率的計算較為準確,PSS2A抑制系統振蕩效果應該不錯。
3 PSS2A低頻抑制效果驗證方法分析
根據 《電力系統穩定器整定試驗導則》[4],PSS2A的效果檢驗有3種方法:負載階躍響應效驗、無故障切除系統擾動效驗和改變發電機組轉動慣量計算低頻段PSS2A作用效驗。因為后2種校驗方法現場操作不便,所以現場一般都采用負載階躍響應試驗來驗證PSS2A抑制效果。但是,采用負載階躍試驗引起的發電機振蕩頻率一般較高,通常在1 Hz以上,此外發電機的振蕩頻率值不易確定,所以對于1 Hz以下的低頻段采用該法一般不容易驗證。為了驗證PSS2A抑制1 Hz以下的低頻振蕩效果,可以采用在機端電壓或電壓給定值上疊加一正弦擾動信號來驗證,根據PSS2A要抑制的振蕩頻率值,可以調節疊加的正弦擾動信號的頻率來實現,通過這種方法可以很方便地驗證出PSS2A在系統1 Hz以下任意具體低頻值的抑制效果。
為了驗證以上所提方法的可行性,在國電南瑞科技股份有限公司所研制的勵磁調節器上進行試驗,采用在電壓給定值上疊加正弦擾動信號,抑制頻率分別是在1 Hz和0.7 Hz,其錄波波形如圖4和圖5所示。
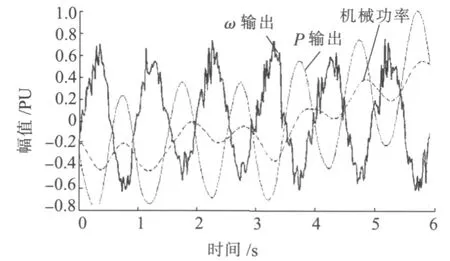
圖4 1.0 Hz擾動錄波曲線
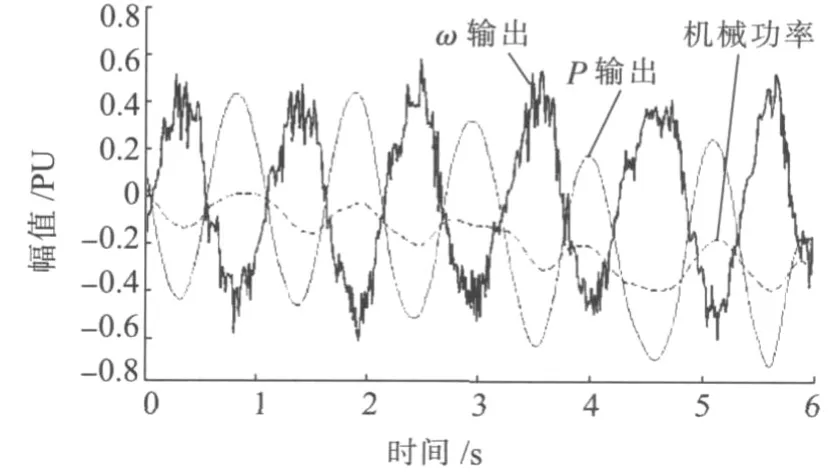
圖5 0.7 Hz擾動錄波曲線
從圖4和圖5看出,P通道輸出與ω通道輸出大小基本相等,相位對應相反,兩者相加后基本抵消,即合成后機械功率較小,高頻濾波輸出(機械功率)應遠小于P輸出(電磁功率),則高頻濾波輸出減去P輸出的差值(加速功率)的計算也較為準確。試驗結束后,比較有PSS和無PSS的振蕩峰峰值之比,如圖6所示,投入PSS時有功峰峰值明顯小于PSS退出時的值,表明PSS對于0.7 Hz的振蕩產生了抑制的效果。
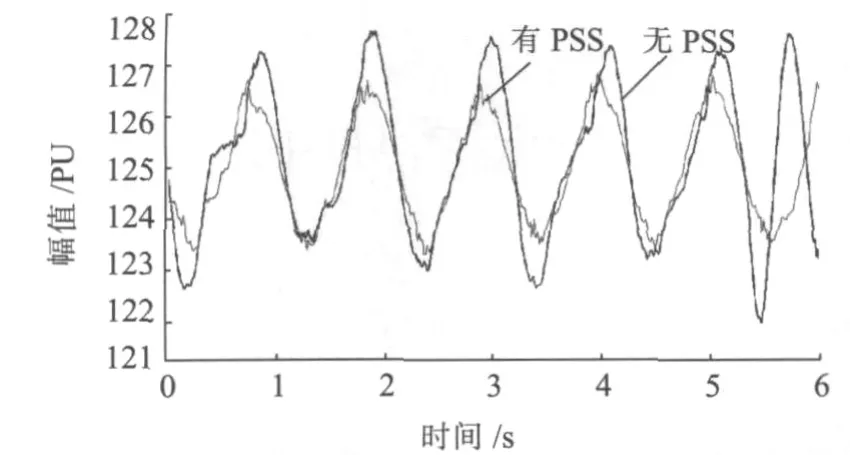
圖6 0.7 Hz PSS投退錄波曲線
需要注意的是,由于不同頻率下對應的PID+PSS幅頻特性不同,因此輸入正弦信號時,不同頻率所需的信號大小也不同,在該機振蕩頻率附近尤其需要注意,逐漸增加正弦信號量,使觀察到的有功功率曲線基本為正弦波且波動明顯大于機組擾動,同時保證無功功率波動在許可的范圍內。所加的正弦波最小頻率只需到系統振蕩模式最低頻率即可。
4 結束語
近年來電網低頻振蕩時有發生,通過目前通常采用的電壓階躍試驗方法并不一定能完全驗證出PSS2A對系統在1 Hz以下的低頻振蕩抑制效果,而且對這方面討論的文獻也不多見,鑒于此情況,希望對1 Hz以下的PSS2A抑制效果驗證方法能夠提供一定的借鑒和思路。
[1]方思立,朱 方.電力系統穩定器的原理及其應用[M].北京:中國電力出版社,1996.
[2]許其品,胡先洪,陳小明.雙輸入電力系統穩定器實現方法探討[J].水電自動化與大壩監測,2008,32(5):8-11.
[3]方思立,蘇為民.電力系統穩定器配置、構成、參數計算及投運試驗[J].中國電力,2004(10):8-13.
[4]Q/GDW143—2006,電力系統穩定器整定試驗導則[S].

