電力系統電壓穩定控制方法的發展與應用

李 楠，謝海英，張天舒

(1．遼寧省電力有限公司電力科學研究院，遼寧 沈陽 110006;2．東北電力第三工程公司，遼寧 錦州 121001;3．金山能源有限公司，遼寧 沈陽 110006)

隨著科技進步和經濟的不斷發展，電力負荷和電網容量迅速增加，電力工業向“大系統、超高壓、遠距離、大容量”發展。但隨之而來的電壓穩定問題愈加明顯，引起業界廣泛關注。近幾十年來，世界各地發生了許多由于電力系統失穩導致的電力系統大面積停電事故，不僅造成巨大的經濟損失，而且影響社會穩定。因此電壓穩定性分析是電力系統運行面臨的重要而復雜的任務。

1 電力系統電壓穩定理論研究方法

電壓穩定問題研究方法主要是基于潮流方程的靜態電壓穩定分析方法和基于狀態方程的動態電壓穩定分析方法。靜態電壓穩定分析方法是基于潮流或擴展潮流方程的分析方法，動態電壓穩定分析方法是建立在微分代數方程 (DAE)的基礎上。電壓穩定基于靜態的分析方法較為成熟，而且應用廣泛，但隨著研究的不斷深入，電壓穩定問題逐漸被認定為本質上是一個動態穩定問題。由于動態負荷模型眾多，各種模型仿真對電壓穩定的影響結果各不相同，關于動態電壓穩定理論與靜態電壓穩定的研究相比仍然不夠完善。

1.1 靜態分析方法

靜態安全指標分為運行點的狀態指標和基于過程的裕度指標。運行點的狀態指標反映了系統鄰近崩潰點的某些特征，通過計算當前運行點的相應量間接評價系統當前運行狀態與穩定極限的鄰近程度。基于過程的裕度指標是通過當前電壓穩定運行點與穩定極限點的差值，判斷當前狀態與失穩狀態的直接距離。主要方法包括潮流多解法、奇異值分解、特征值分析法、模式分析法、連續潮流拓展法、最大功率法和靈敏度法等。

利用潮流多解法計算靜態安全狀態指標可以判斷系統電壓穩定狀態。潮流方程為一個非線性方程，可能存在多個實數潮流解，隨著負荷的不斷增加，其潮流解的對數越來越少，最后只剩下一對潮流解，高電壓解和低電壓解。高電壓解和低電壓解均值正好是系統電壓穩定臨界點處的電壓值，低電壓解被證明為不穩定解。系統電壓穩定狀態可通過計算高電壓解與低電壓解的距離判斷，但該方法對低電壓解很難求取。靈敏度法是通過計算在某種擾動下，采用系統變量對擾動的靈敏度來判斷系統的穩定性。潮流方程表示為［1］

式中 α——參數變量;

X——狀態變量;

U——控制變量;

Y——輸出變量。

根據不同靈敏度，利用基本方程對控制變量U、參數變量α求全微分:

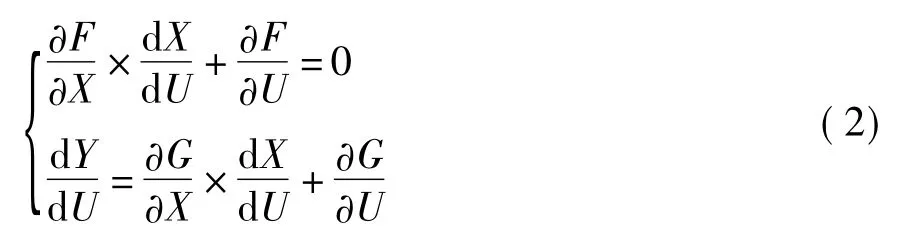
將式 (3)在平衡點X0處泰勒展開略去高階項得:ΔZ=Fx×ΔX=JRΔX，對JR進行奇異值分解，設 JR非奇異，得:VTJRU=diag(δ1，δ2，……，δn)，代入泰勒公式得:ΔX=U×Λ－1×VT得:由于最小奇異值在F范數意義上反映了矩陣至矩陣奇異之間的最短距離，因此，利用矩陣最小奇異值可以表示當前系統與靜態穩定極限之間的最短距離。但雅可比矩陣的非線性，不易提供對系統穩定裕度的預測。最大功率法是基于網絡能夠傳送功率的極限而求取電壓穩定的方法，當負荷需求超過網絡所能傳輸的功率極限時，將這一臨界運行狀態稱為電壓穩定極限運行狀態，求臨界點是該方法的關鍵。連續潮流法是解決臨界點的求取方法，通過引入一維校正方程，消除了潮流雅可比矩陣奇異現象，使該方法得到廣泛應用。由于獲取臨界點需要的計算量很大，計算速度較慢，不適于在線應用。

靜態研究方法在獲取電網極限運行狀態、指導生產調度等方面發揮了重要作用，為動態分析方法的研究奠定了基礎。

1.2 動態分析方法

隨著研究的不斷深入，電壓穩定問題的動態本質引起了人們的重視，人們逐漸認識到要從根本上解釋電壓失穩機理必須建立電力系統的動態模型，用各種動態分析方法來研究電壓崩潰現象的物理本質，目前電壓穩定性分析的動態方法主要有小干擾分析法、時域仿真法、動態潮流法等。

少擾動分析法主要步驟是根據研究對象考慮恰當的動態元件，建立描述系統動態過程的模型，列出系統微分—代數方程 (DAE)，在平衡點將DAE線性化，消去方程中的非狀態變量，得到線性化微分方程，然后根據線性化微分方程雅可比矩陣特征值的實部判斷系統的穩定性。但小擾動穩定分析方法計算量較大，實際的電力系統穩定分析中較多采用靜態方法。當系統遭受大擾動時必須采用時域仿真法對電壓穩定性進行研究。時域仿真法采用數值分析方法進行研究，得到電壓及一些變量隨時間變化曲線，該方法具有較高的建模精度和分析結果。

暫態電壓穩定分析可分為時域仿真法、李雅普諾夫直接法及擴展等面積準則。但時域仿真速度較慢，李雅普諾夫直接法需要積分到擾動消失，在工程應用中受到一定限制。擴展等面積準則采用靈敏度分析技術，避免了大量的積分試探而直接估計極限值，提高了仿真過程的計算速度。當電壓失穩過程持續很長時間時，必須進行中長期電壓穩定研究。針對長期電壓穩定特點，Dr．Van Cutsem提出快速時域仿真法QSS。QSS仿真算法認為在長期電壓不穩定的情況下，發電機及其調節器的動態響應為瞬時響應，平衡方程代替了發電機及調節器的動態方程，其模型由電壓穩定分析的系統多時標方程演化而來。

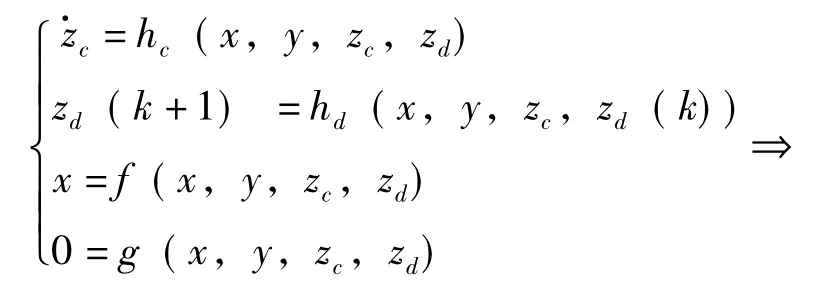
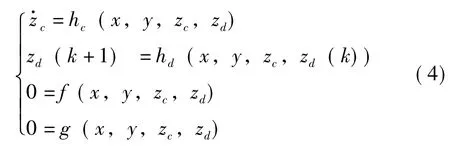
式中 x——發電機和調節器的狀態向量;

y——網絡節點電壓向量;

zc——與負荷動態相關的連續狀態向量;

zd——OLTC的變比等離散變量。

QSS仿真求解步驟是尋找長期動態發展過程中的一系列暫態平衡點，在每個時間步長上暫態平衡點的求取就是快動態變量x、y對慢動態變量zc、zd變化做出響應。QSS仿真算法能反映控制作用和元件動作的時域規律，計算速度快、收斂性好。文獻［2］提出將直接法應用于帶參數的QSS仿真系統模型中，解決系統極限求取中QSS方程在崩潰點附近存在病態問題。

1.3 靜態分析與動態分析的關系

數學上的分岔理論研究非線性系統在參數變化下是否能保持原來系統穩定性的問題，而靜態電壓穩定問題可視為系統在不同負荷水平下發生分岔的問題。分岔理論建立了系統分岔與系統穩定性的關系。靜態電壓穩定臨界點與動態分析下的SN分岔點是一致的，在這一基礎上，靜態分析方法可有一動態的解釋。

高階電力系統動態特性可用與系統參數有關的非線性微分—代數方程組描述［3］:

式中 f——代表系統;

g——潮流方程;

X——系統狀態變量;

Y——除狀態變量以外的其他變量;

p——系統參數和操作參數。

對于每一組確定的系統參數p，系統平衡點X*是式 (5)的解。小擾動線性化形式為

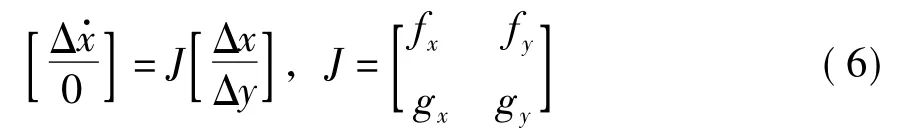
對于系統的結構性穩定問題，雅可比矩陣特征值的實部決定系統在某個平衡點的穩定性，出現正實部則系統不穩定。鞍結分岔Hopf分岔所隱含的假設為gy不奇異。如果參數逐漸變化到gy奇異時，雅可比矩陣的特征值改變符號。當特征值由－∞→+∞，表現為單調失穩，系統發生奇異誘導分叉，此時小擾動方程式無解［1］。提出暫態穩定分析方法，可通過引入一個很小的正常數ε，利用奇異擾動方法處理代數方程，得到奇異擾動形式的微分方程模型:X·=f(X，Y，P)，εY·=g(X，Y，P)，原DAE的奇異點將消失。

2 電力系統電壓穩定的控制

電壓穩定控制按類型可分為緊急控制和預防控制。根據電壓靜態穩定分析理論和電網運行的經濟角度，電力系統穩定運行時，應保持一定的電壓穩定裕度，對電力系統電壓穩定進行預防控制。通過改變網絡參數、增加系統所需無功容量等方式，使運行狀態遠離電壓穩定的臨界狀態，保持電壓質量穩定。當線路及變壓器傳輸功率時，由 ΔU=可知，傳輸無功功率將引起電壓降落，需要改變網絡參數，串聯電容及無功補償設備，抵消部分電抗，達到保持電壓穩定的作用。當系統發生小擾動而進入弱穩或不安全區域時，通過無功功率控制或減輕系統負荷的方式使系統進入穩定區域。

在電力系統出現故障等特殊的情況下，電壓穩定裕度不足甚至趨于電壓崩潰時，如何通過各控制器的協調動作，最大限量地確保負荷供電，為恢復創造良好條件是目前重要研究課題。目前常用的方法主要有改變系統潮流、投入無功補償裝置、改變有載調壓變壓器 (OLTC)的電壓設定點、甚至切除部分負荷，保證電壓的穩定性。當系統中局部節點負荷變化較大時，需要適時調整無功電源保持電網電壓穩定。在電網中無功電源主要由發電機及無功補償裝置組成，無功補償裝置包括投切并聯電容器、調相機、SVC、SVG裝置。發電機不僅是有功電源，也是無功電源，可以通過發電機的自動勵磁調節設備自動調整發電機的機端電壓、分配無功功率。對于發電機直接供電的負荷，如果線路不長、電壓損耗不大，可以直接通過發電機調壓就能滿足負荷電壓要求。如果通過多級變壓供電，需照顧距離發電機近處的負荷，電壓不能調的過高，遠處的負荷還要靠有載調壓變壓器等措施解決。依靠OLTC控制電壓質量在某種情況下不利于電壓穩定，OLTC和發電機過勵限制等慢動態裝置相互作用可能引起電壓失穩。如果系統發生罕見的嚴重復雜故障，導致系統趨于電壓崩潰，如果不能保持系統穩定運行，則必須有選擇地切除部分負荷，防止系統崩潰［4］。由于電網系統故障的復雜性，當電網瀕于崩潰時，為做出快速準確判斷切除負荷達到電網穩定的目的，很多地方已將大停電防御體系應用到實踐中，并取得了積極的效果。

3 結束語

目前，對電力系統電壓穩定分析的研究仍主要集中在動態分析方法及電壓崩潰機理的研究，預防電壓崩潰的發生、確定合適的無功儲備和穩定裕度、校驗緊急控制策略的優劣、在線生成控制策略、確定保護系統的協調動作等仍有待進一步研究。

［1］ 周雙喜，朱凌志，郭錫玖，等．電力系統電壓穩定性及其控制［M］．北京:中國電力出版社，2004．

［2］ 安 寧，陳興雷，任 瑞，等．基于準穩態分析求取中長期電壓穩定極限新方法［J］．電力系統保護與控制，2011，39(18):1－7．

［3］ 王慶紅，周雙喜．電力系統微分代數模型奇異誘導分岔分析［J］．中國電機工程學報，2003，23(7):18－22．

［4］ 程浩忠，吳 浩．電力系統無功穩定性［M］．北京:中國電力出版社，2004．

［5］ 袁季修．電力系統安全穩定控制［M］．北京:中國電力出版社，1996．

［6］ 段獻忠，袁 駿，何仰贊，等．電力系統電壓穩定靈敏度分析方法［J］．電力系統自動化，1997，21(4):9－12．