基于博弈論的動態頻譜分配技術研究*

徐昌彪,劉雪亮,鮮永菊

(重慶郵電大學 測控與信息傳輸實驗室，重慶400065)

隨著無線通信技術的發展，尤其是隨著無線局域網WLAN(Wireless Local Area Network)及無線區域網絡WRAN(Wireless Regional Area Network)等技術的發展，人們對無線通信業務需求的不斷增加與無線頻譜資源的匱乏之間的矛盾越來越尖銳。針對頻譜資源的不足，認知無線電網絡中的動態頻譜分配技術能夠靈活地使用空閑頻譜[1]，實現空閑頻譜的再利用，從而提高頻譜利用率。為了達到這一目的，認知無線電需要擁有感知周圍環境以及根據周圍環境的變化自適應地調整系統參數的能力，從而能夠感知到授權用戶的空閑頻譜并利用其進行通信。然而，授權用戶和非授權用戶在授權頻段的和平共存是一個具有挑戰性的課題。目前，認知無線電系統的頻譜分配研究方法很多，基于博弈論[2]的頻譜分配方法是研究的熱點。參考文獻[3,4]中用博弈論分析了主用戶相互競爭提供頻譜的行為，主用戶根據次用戶的頻譜需求大小以及其他主用戶所采取的策略動態調整自身的策略，從而使得自己的效用達到最大化，而對次用戶之間競爭頻譜的博弈行為沒有考慮。參考文獻[5,6]中應用寡頭市場模型來解決頻譜分配中授權用戶的博弈問題，并用Bertrand均衡理論提出了授權用戶信道競價的Bertrand博弈算法。參考文獻[7]中考慮了基于用戶業務需求的頻譜分配，根據用戶的業務等級不同進行頻譜分配。參考文獻[8]中用博弈理論分析認知網絡中多個策略主用戶與多個策略次用戶的博弈問題,主用戶的頻譜價格是通過AP唯一確定的，但在實際的認知無線電環境中，主用戶的頻譜價格是不斷變動的。參考文獻[9]中提出基于Cournot博弈的次用戶頻譜分配模型，目前，有很多工作基于該文獻進行改進，如在次用戶的頻譜分配中考慮了頻譜差異性對次用戶的影響[10]，考慮頻譜拍賣的多買家、多賣家博弈模型[11]等。在以上模型中，都沒有考慮到主用戶的頻譜價格函數受到主用戶和次用戶之間的頻譜供需關系的影響。

本文用博弈論方法解決認知無線電網絡中的動態頻譜分配問題，將次用戶的頻譜分配模型轉換為相應的博弈論模型，在完全信息和不完全信息環境下，分別用靜態博弈和動態博弈對次用戶的頻譜分配進行分析，并考慮了頻譜可置換參數v對次用戶納什均衡以及動態博弈穩定性的影響,最后給出改進博弈模型的仿真分析結果。

1 系統模型

1.1 認知網絡模型

在認知網絡中，認知用戶能夠伺機利用授權用戶的空閑頻譜。當授權用戶重新占用該頻譜時，認知用戶需要切換到其他授權用戶的空閑頻譜上進行通信。文中考慮有M個授權用戶和N個次用戶的模型，每個授權用戶擁有一個授權頻譜，授權用戶的頻譜占用情況會隨著時間及其空間變化而發生變化。次用戶的行為是自私、理性的，次用戶為了最大化自己的效用相互競爭并最終達到納什均衡。納什均衡點即為次用戶的最佳頻譜分配結果。如圖1所示，基站把所有主用戶的空閑頻譜匯聚成一個頻譜池，將頻譜池中的頻譜劃分為若干個子信道，子信道是頻譜分配的基本單位。主用戶以每單位帶寬價格p向次用戶收費，p是頻譜價格函數,與主用戶提供的頻譜數量以及次用戶的頻譜需求數量有關。

1.2 無線傳輸模型

通過采用自適應調制編碼(AMC)技術，次用戶可以根據信道質量情況動態調整傳輸速率從而適應周圍的環境。采用正交幅度調制技術（如4-QAM和16-QAM），在單輸入單輸出高斯信道噪聲中誤碼率可以近似為：示接收機信噪比，k為所用調制方式的頻帶利用率。不失一般性，設頻帶利用率為非負實數。為了滿足特定的應用需求，BER需要維持在一個目標水平（即目標誤碼率BERtar），次用戶i頻譜傳輸效率為：ki=log2(1+Kγ)。其中K為一個常

2 頻譜分配的博弈模型

首先假定所有次用戶都知道其他次用戶在博弈中所采取的策略以及各自的效用函數信息，并用靜態博弈模型分析次用戶的行為。然而，由于在實際的認知無線電網絡中，次用戶并不知道或只知道一部分次用戶的策略和效用信息，次用戶需要不斷調整自己的策略從而使自身的策略達到最優，因此，用動態博弈模型對次用戶的策略調整行為進行分析。

2.1 靜態博弈

在上面的系統模型中，博弈的參與者是次用戶，策略是次用戶的頻譜請求大小，用bi表示，每個策略用戶的效用函數與它所獲得的總收益以及成本有關，用Ui表示。對參考文獻[9]中的頻譜價格函數進行改進，在主用戶對頻譜價格滿意的基礎上，考慮了頻譜價格受到頻譜供需關系的影響，即與主用戶空閑頻譜的數量以及次用戶的頻譜需求相關。頻譜價格函數為：

其中,w為主用戶單位頻譜的成本價格，N為次用戶的數量;M為主用戶的數量;τ為非負常數，當 τ≥1時，頻譜價格函數是凸的;bi為次用戶i的頻譜請求;qj為主用戶j的空閑頻譜。

次用戶的效用函數選擇不是唯一的，本文要保證頻譜分配算法能夠達到均衡收斂。根據參考文獻[10]中給出的二次效用函數做出適當修改如下：

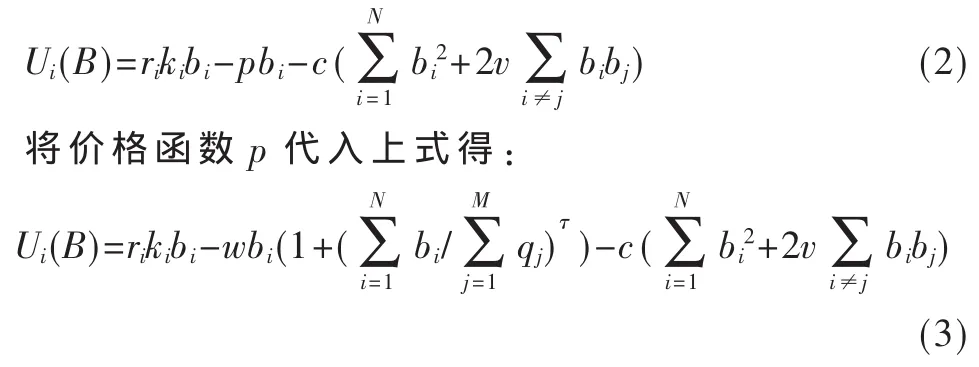
其中,ri為次用戶i單位傳輸速率獲得的收益，ki為次用戶i的頻譜傳輸效率,B為所有次用戶的策略集合，B={b1，b2，…，bN}，c 為一常量。

效用函數中考慮了頻譜置換參數 v，v∈(-1,1）。當v=0時，次用戶不能發生切換;當v=1時，次用戶可以在工作頻段自由切換;當v＜0時，次用戶共享的頻譜是互補的,即當一個次用戶使用一段頻譜時，它需要同時購買一個或多個額外的頻譜（也就是說，一段頻譜用于上行鏈路傳輸，另一段用于下行鏈路傳輸，這些頻譜可能來自同一個主用戶或不同主用戶的頻譜）。

根據式(3)中得到的效用函數，將次用戶i的效用函數對bi求偏導，即可得到次用戶i的邊緣收益函數：

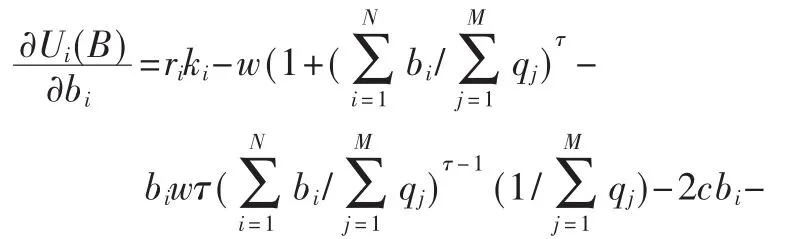
令邊緣收益函數等于0，即可求得次用戶i的最佳響應函數為：

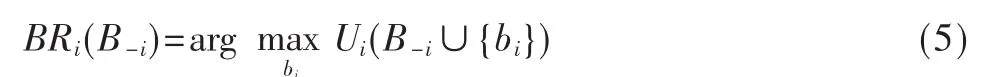
B-i表示除次用戶i之外所有次用戶的策略集合，當且僅當bi*=BRi(),?i，次用戶的博弈達到納什均衡，納什均衡解為 B*=,…,)，表示除次用戶 i之外所有次用戶的最佳策略組結合。

2.2 動態博弈

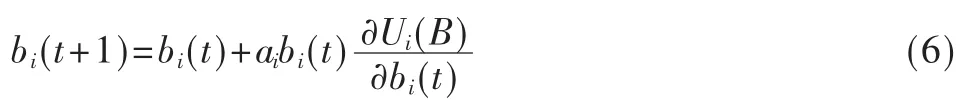
其中，bi(t)為次用戶 i在時刻 t的頻譜請求，αi為次用戶i的速率調整參數（即學習速率）。當bi(t+1)=bi(t)時，次用戶的動態博弈達到均衡，此時，次用戶的策略不再發生變化。

由于在實際的認知無線電環境中，次用戶只能觀察到主用戶的頻譜定價信息，并不知道其他次用戶所采取的策略以及它們的效用信息，所以每個次用戶只能根據歷史博弈信息選擇自己的策略。這意味著，次用戶采用分布式算法動態調整自己的頻譜請求大小并最終達到納什均衡。在這種不完全信息的情況下，次用戶需要不斷調整自己的策略從而使得自身的策略達到最優。次用戶的頻譜請求可以用動態博弈來描述：

2.3 動態博弈的穩定性分析

在動態博弈算法中，次用戶之間的博弈最終將達到納什均衡，納什均衡的穩定性與學習速率αi有關。通過使用雅克比矩陣和本征值的概念，可以研究文中提出的動態博弈算法的穩定性。當所有的本征值(λi)都位于單位圓內時(|λi|＜1),博弈的結果是穩定的。

雅克比矩陣定義如下：

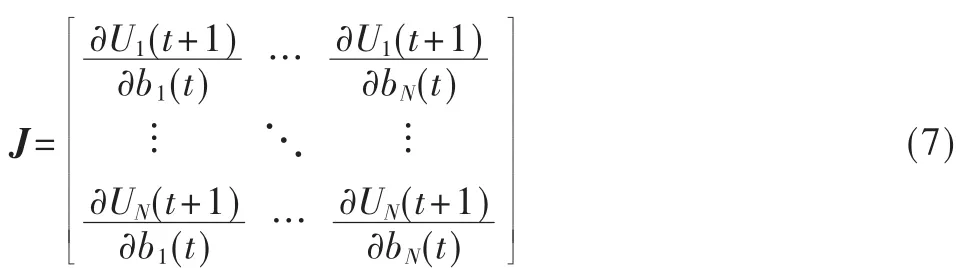
假定有兩個次用戶存在的情況下，通過求解下面方程得到雅克比矩陣的本征值：

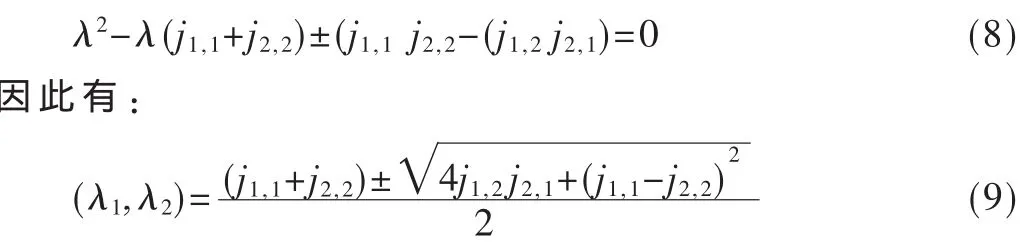
3 仿真分析

文中假設在一個認知無線電系統中有4個空閑的主用戶頻譜和多個次用戶，每個主用戶擁有的頻譜為6 MHz。主用戶單位頻譜的成本價格w為5，目標誤碼率BERtar為 10-4，采用線性定價，參數 τ設置為 1，c為 0.5，次用戶每單位傳輸速率所獲得收益為ri=10，?i。

3.1 次用戶的最佳響應以及納什均衡

圖2是兩個次用戶的最佳響應函數曲線，一個次用戶的最佳響應是其他次用戶策略的線性函數，納什均衡點位于次用戶最佳響應函數曲線的交叉點。

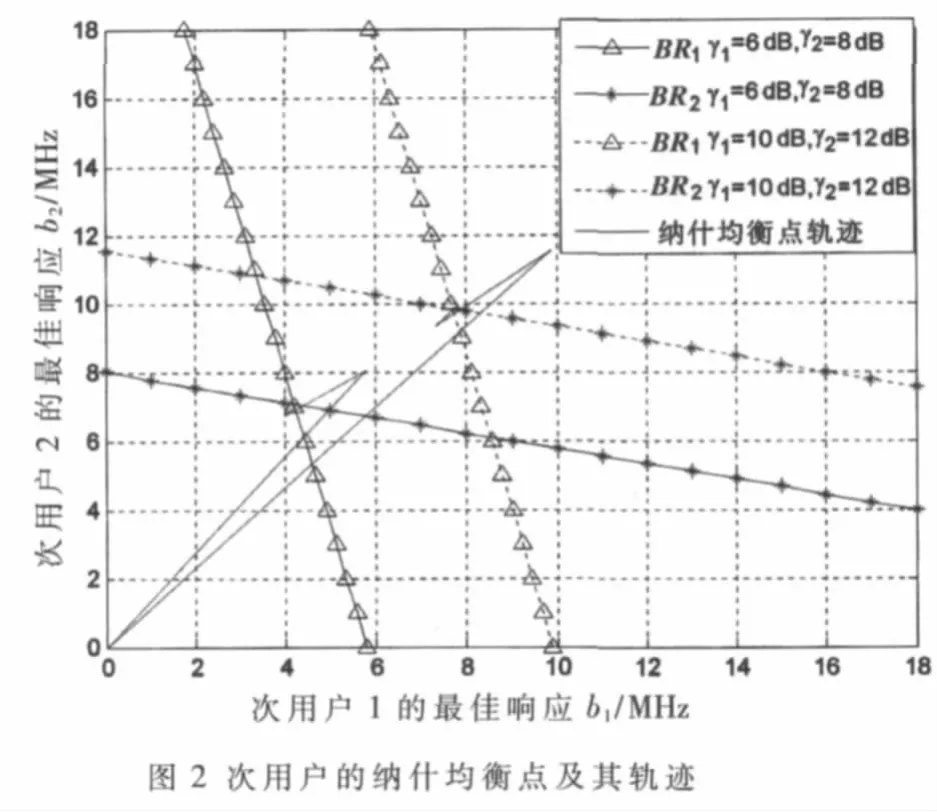
圖中納什均衡點的位置與信道質量有關，信道質量越好，次用戶的效用越大，頻譜需求也越大。由于次用戶之間是自私的并相互競爭頻譜，所以，一個次用戶的信道質量的好壞會影響其他次用戶的策略。當一個次用戶的信道質量變好時，它希望得到的頻譜更多。而在實際的認知無線電系統中，主用戶的空閑頻譜是有限且隨時間發生變化的，所以，次用戶之間的頻譜競爭會更加激烈從而影響它們所采取的策略。

3.2 次用戶的效用

圖3中顯示了在次用戶1的信道質量一定的情況下，次用戶1和次用戶2的效用與次用戶2的信道質量相關，隨著次用戶2的信噪比不斷增加，次用戶2的信道質量越好得到的頻譜會越多，因此次用戶的收益會隨著次用戶2的信噪比的增加而增加。由于次用戶1與次用戶2之間是競爭的關系，次用戶2得到的頻譜越多，次用戶1得到的頻譜相應就會減小，因此，次用戶1的收益會隨著次用戶2信噪比的增加而隨之減小。

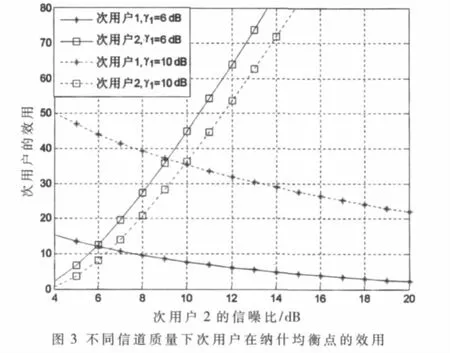
3.3 次用戶的動態博弈

在實際的認知無線電中，由于次用戶的策略和效用等信息相互之間不知曉，次用戶根據歷史博弈信息動態調整自己的策略并最終收斂到納什均衡。圖4顯示了次用戶策略的動態調整過程。從圖中可以看出，動態博弈算法的收斂性與學習速率αi有關,設置合適的學習速率可以使博弈快速收斂到納什均衡，當學習速率過大時，次用戶的策略波動很大，甚至不能達到納什均衡。當α1=α2=0.15時，次用戶1和次用戶2的策略能夠較快地收斂到納什均衡，而當α1=α2=0.22時，次用戶1和次用戶2的策略一直上下波動，不能較快收斂到納什均衡。圖5顯示了多個次用戶存在時動態博弈的收斂情況，可以得出，當次用戶的數量增加時，每個次用戶得到的頻譜數量減少，博弈達到收斂的時間隨之增加。

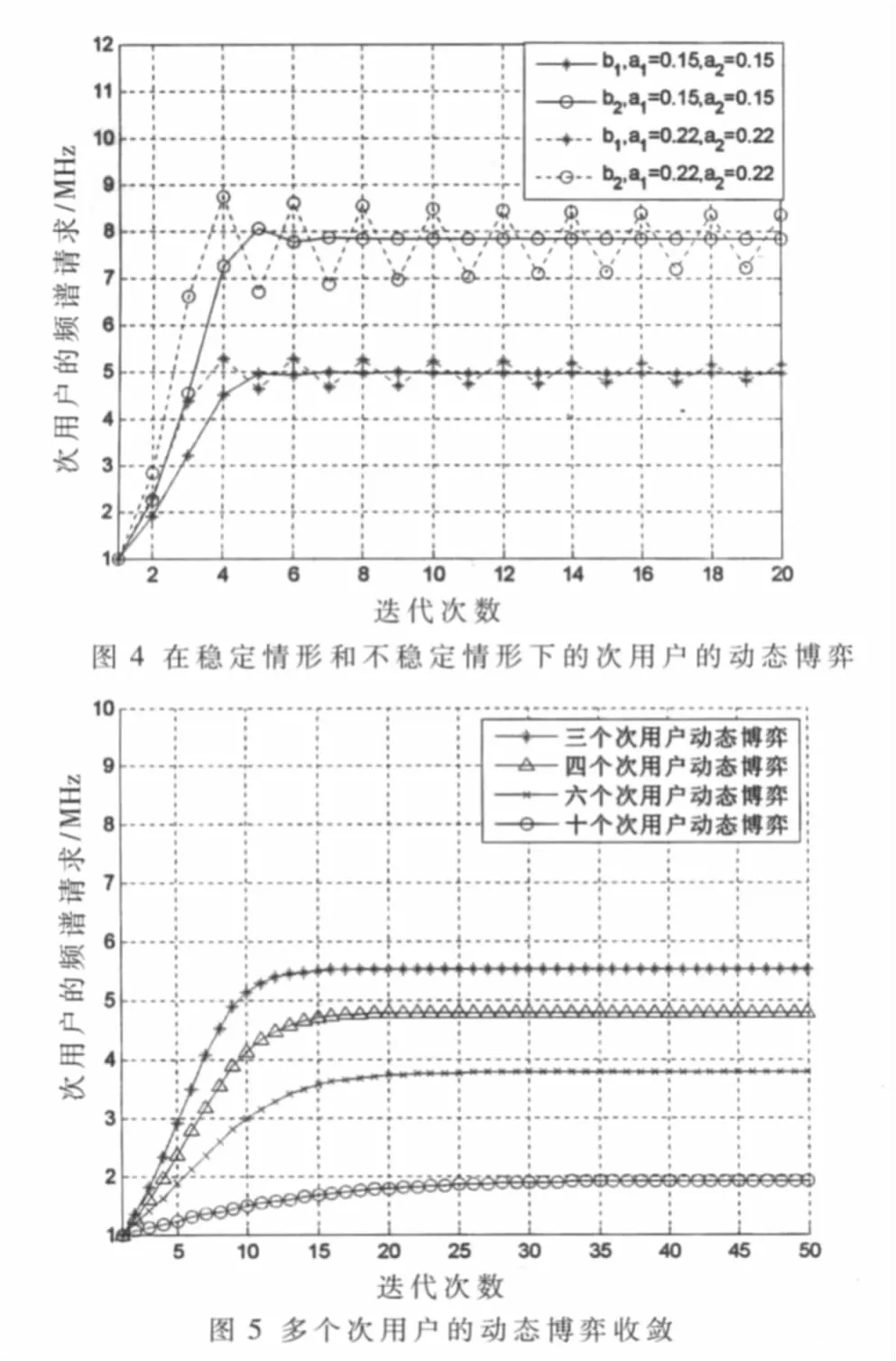
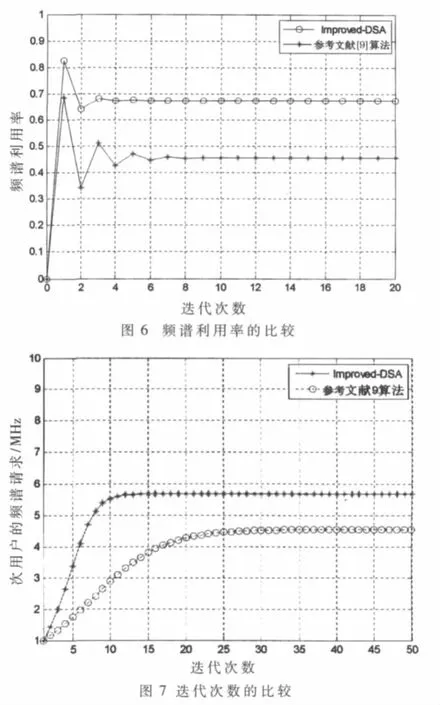
圖6和圖7分別從頻譜利用率和次用戶收斂到納什均衡的時間與參考文獻[9]的博弈算法進行比較，不難得出，本文提出的算法的頻譜利用率高于參考文獻[9]中的算法，并且能夠更快收斂到納什均衡。這里的頻譜利用率定義為認知無線電系統中所有次用戶得到的總頻譜與所有主用戶的空閑頻譜之比。

3.4 次用戶動態博弈的穩定區間

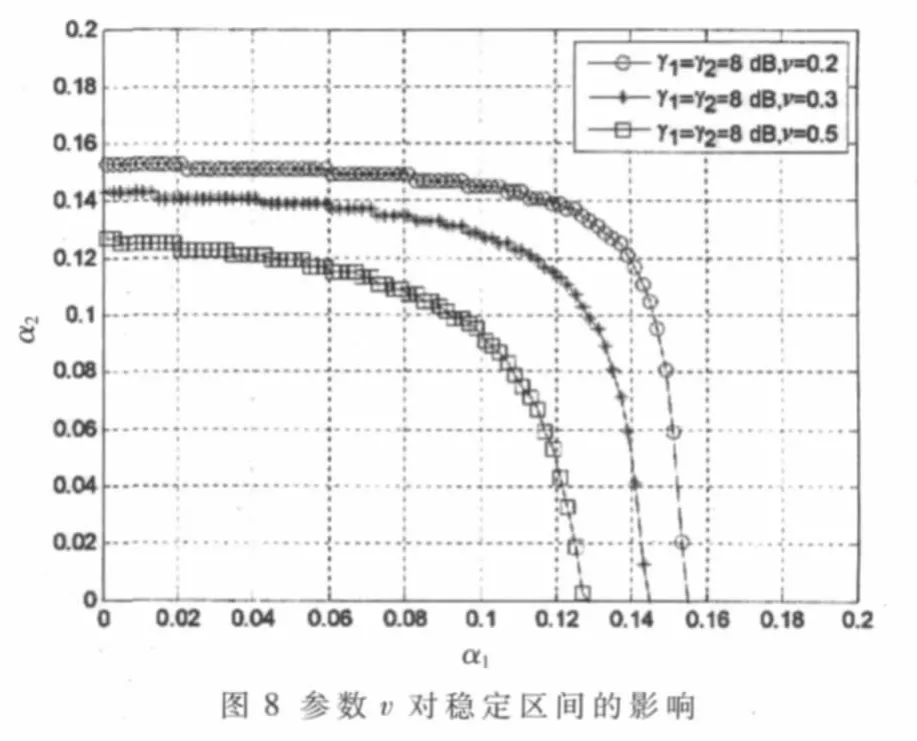
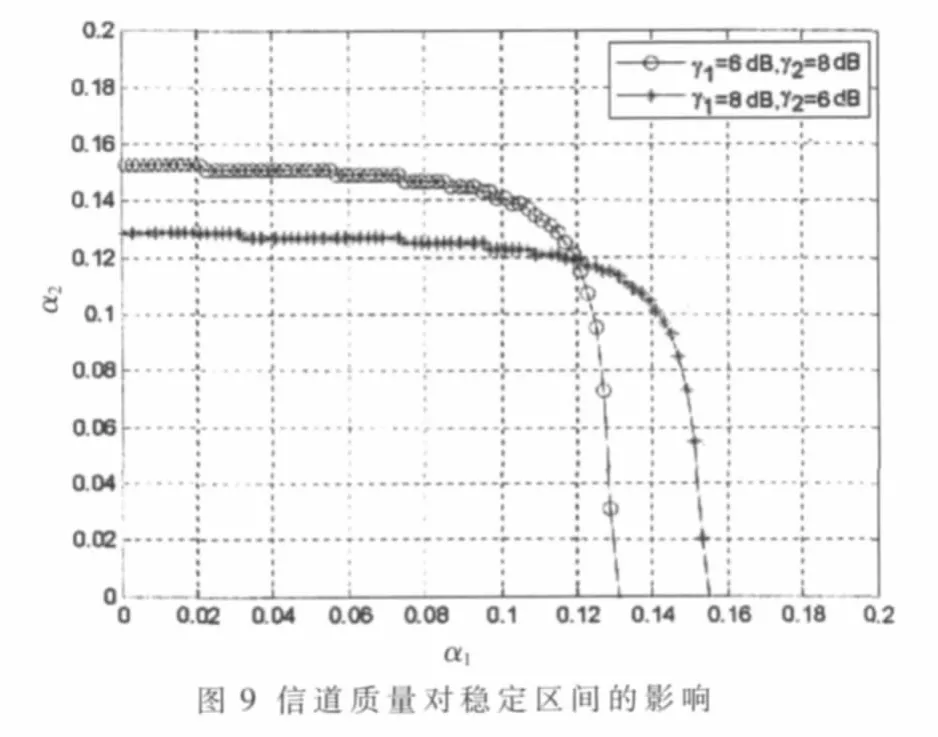
根據式(7)中得到的雅克比矩陣本征值，可以得到α1與α2之間的關系。從圖8中可知頻譜置換型參數ν對穩定區域的影響：ν值越大，次用戶動態博弈的穩定區間越小,穩定區域指的是α1與α2之間的關系曲線和坐標軸之間所圍成的區間。圖9顯示了穩定區間還與信道質量有關，信道質量越好，穩定區域會越小。當α1與α2在穩定區間內取值時,次用戶間的頻譜共享是穩定的并最終可以達到納什均衡,而在區間外取值時，次用戶的策略會上下波動進而導致無法收斂到納什均衡。

文中提出了一種改進的基于博弈論的動態頻譜分配方案，考慮了存在多個主用戶和次用戶共享頻譜的情形，在保證不對主用戶產生干擾的前提下，利用Cournot博弈模型對次用戶間的競爭頻譜行為進行了分析。改進了現有的頻譜定價函數，并在次用戶的效用函數中考慮了頻譜置換參數v。最后分別用靜態博弈和動態博弈分析了次用戶的頻譜分配行為。通過仿真驗證證明，次用戶的策略能較快收斂到納什均衡，并且頻譜利用率有一定的提高。

[1]MITOLA J.Cognitive radio for flexible multimedia communications.in Proc.MoMuC’99，1999:3-10.

[2]FUDENBERG D,TIROLE J.GAME T.Mit Press,1991.

[3]MOHAMMADIAN H S,ABOLHASSANI B.Optimal quality competition for spectrum sharing in cognitive radio networks[C].Electrical Engineering(ICEE),2010:231-236.

[4]Zu Yunxiao,Li Peng.Study on spectrum allocation of primary users for cognitive radio based on game theory[C].in IEEE WiCOM.2010:1-4.

[5]譚學治，劉玉濤，魏守明.基于博弈理論的認知無線電頻譜分配[J].華南理工大學學報,2010(5):22-26.

[6]NIYATO D，HOSSAIN E.Competitive pricing for spectrum sharing in cognitive radio networks：dynamic game，inefficiency of nash equilibrium and collision[J].IEEE Journal on Selected Areas in Communications,2008,26(1):192-202.

[7]He Shibiao,Zhang Xinchun,Ge Lijia,et al.Research of dynamic spectrum allocation based on service demand[C].in IEEE NSWCTC,2010:348-351.

[8]Lin Peng,Jia Juncheng,Zhang Qia.Mounir ham di dynamic spectrum sharing with multiple primary and secondary users[J].in IEEE Transactions on,2011(60):1756-1765.

[9]NIYATO D,HOSSAIN E.Competitive spectrum sharing in cognitive radio networks:a dynamic game approach[J].IEEE Transaction on Wireless Transaction on Wireless Communications,2008,7(7)：2651-2660.

[10]Zhang Xinchun,He Shibiao,Sun Jiang.A game algorithm of dynamic spectrum allocation based on spectrum difference[C].in IEEE WOCC,2010:1-4.

[11]NIYATO D,HOSSAIN E,HAN Z.Dynamics of multipleseller and multiple-buyer spectrum trading in cognitive radio networks:a game-theoretic moeling approach[J].Mobile Computing,IEEE Transactions on,2009,8(8):1009-1022.