卡爾曼濾波在紅外尋的導彈被動制導中的應用
龔冬梅,張海濤,龔 梅
(中國空空導彈研究院,河南 洛陽 471009)
隨著科技特別是航空航天技術的發展,空中目標機動突防性能逐漸提高,其攔截問題引起了世界各軍事強國的普遍重視[1]。早期的攔截器由于彈載計算機計算速度慢以及古典導引律本身缺陷等原因而使得制導精度不高,致使其無法在實戰中應用。因此,從20 世紀的70年代起,依靠狀態空間法、變結構理論以及其他智能方法等發展起來的先進制導律在理論研究中表現出比傳統比例導引律具有明顯的優點,主要表現是理論嚴謹,命中精度很高。但這些先進制導律優點明顯,但缺點同樣顯著,其使用的前提需要目標以及導彈的狀態信息多,這在實際應用中相當困難,尤其是對于紅外空空導彈來說,僅能夠測量出角度和角速度信息,而彈目相對距離、相對速度和目標加速度信息無法測量,只能靠估計得到。這些僅利用角度信息來估計出彈目相對運動狀態信息實際上就是一個濾波問題。本文利用最優卡爾曼濾波方法,對僅有的失調角信息進行濾波狀態估計[2-5],在簡化制導回路上以古典比例導引律和擴展比例導引律為例,進行數值仿真,計算結果表明,將通過濾波估計出的彈目相對速度,視線角速度和目標加速度等信息應用于擴展比例導引律的系統與純比例導引律相比,具有更小的脫靶量。
1 目標運動方程的建立
目標運動參數估計方程在慣性系中建立,采樣時間設計為Ts,將方程離散化:
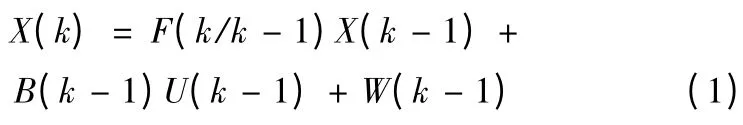
即狀態方程為:

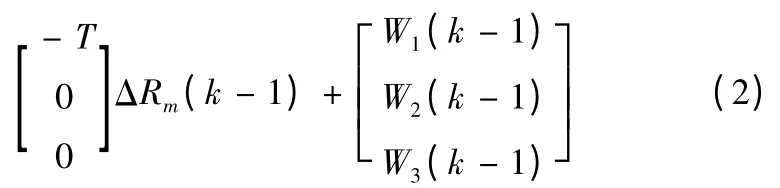
式中:ΔRm、TT、T、W 分別為導彈速度增量、目標機動時間常數、步長、狀態噪聲。
其中目標機動模型采用一階馬爾科夫過程的假設
測量方程:
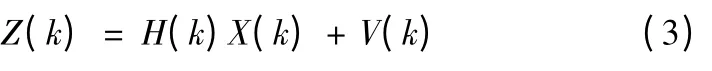
即:
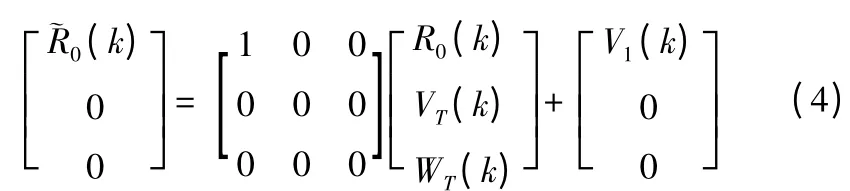
式中~R0、V1分別為相對距離測量量和量測噪聲。
導引頭對目標的探測信號中含有多種噪聲,即狀態噪聲w 包括背景噪聲、熱噪聲、電磁噪聲、探測噪聲等,對于采用比例導引的導彈,導引頭量測誤差v 主要有目標相對導彈的視線角速度的量測誤差,失調角零位的測量誤差,引起失調角零位測量誤差的因素較多,如導引頭信息處理誤差,導引頭裝配誤差,通道耦合誤差,干擾、背景引起的誤差,彈體耦合誤差,陀螺回轉中心與位標器質心不重合引起的漂移,隨動機構間隙等,這些因素都會引起信號測量值的波動。因此,為提高制導精度,加強對大機動目標的攻擊能力,在制導回路中加入濾波算法以保持制導信號的穩定以及制導狀態信息的重構就顯得尤為重要。
2 卡爾曼濾波器設計
采用卡爾曼濾波公式,其最優濾波方程為:
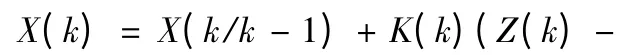

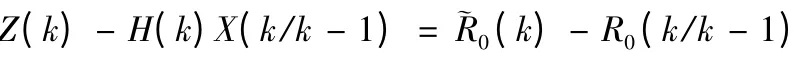
為誤差方程。
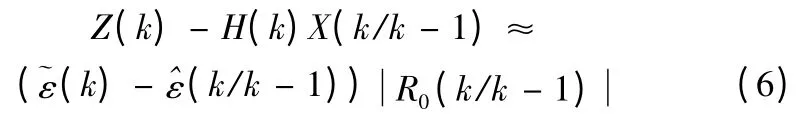
可得濾波方程:
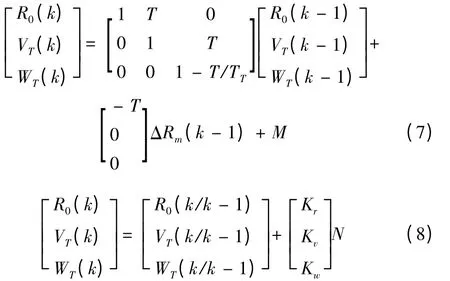
其中:

在此模型中,視線角的測量包含有噪聲,通過將視線角測量值與導彈到目標距離的估值相乘可以產生相對位置的偽測量值,通過卡爾曼濾波器產生相對位置、相對速度和目標加速度的最優估值,如圖1 所示,量測值~εR 是光軸與真值之間的距離,估值^εR 是估值與光軸之間的距離,線偏離ΔRI=(~ε+Δ~ε)R-^εR,在導引頭成像系統中,伺服機構驅使光軸跟蹤真實值,而估值通過線偏離的校正始終跟隨光軸運動,所以在濾波角通道系統中,只要準確估計出DRI,可得到Y,Z 向上的狀態。
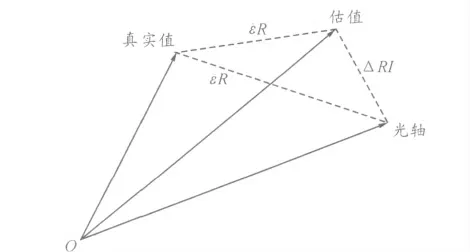
圖1 真實值與估值之間的關系
由于ε 在慣性系中,因此在使用時要轉到視線系,這就實現了相對距離、目標速度、目標加速度和失調角的卡爾曼濾波估值。工程實際使用時,要考慮濾波門限的選取、距離分檔、測量噪聲的設計和目標類型等因素對協方差陣P 的影響,要對協方差陣P 調整以保證濾波的精度和收斂性。
3 數值仿真
仿真條件如下:狀態和量測方程如上所述,仿真時間從0 ~10 s,采樣時間ts=0.01 s,輸入為正弦信號,狀態噪聲Q和量測噪聲R 的方差為0.4 和1,即w =sqrt(Q)* randn(n,1),v=sqrt(R)* randn(n,1),濾波增益陣的初值Mn=設為zeros(3,1),P 陣和x 的初值分別為B* Q* B'和zeros(3,1),濾波后的波形,量測噪聲,卡爾曼濾波增益,卡爾曼濾波協方差陣的仿真結果如圖2 所示。
經過數字仿真分析可以得出,在量測修正得當的前提下,卡爾曼濾波值可以準確并平滑的估計出狀態變量,模型具有較小的超調時間,當采樣間隔越小時,估值越平滑,越接近真實值,初始協方差陣P 是在解Ricatti 方程式中使用的,其初值對濾波具有很大的的影響,噪聲越小濾波估值越準確,狀態噪聲增大時會嚴重影響到濾波的效果,在工程實際運用中噪聲加入要考慮到敏感器件的實際情況。
有了這些狀態信息,就可以改進導引律設計,以擴展比例導引律為例:
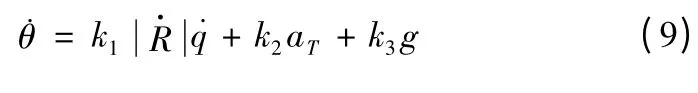
由脫靶量可以看出,從近距到中距,大離軸角發射,目標作6 ~9 個g 大機動飛行時,制導系統中加入濾波比純比例導引脫靶量顯著減小,有了濾波的準確估值可以大大改進制導系統的精確度,濾除噪聲增加系統的穩定性。
4 結束語
本文主要研究了僅有角度測量信息的紅外尋的導彈被動制導問題,給出了基于最優卡爾曼濾波的目標運動狀態估計方法,并給出了簡化制導回路下加入濾波擴展比例導引和不加濾波比例導引兩種情況下制導系統仿真,可以得出以下結論:
(1)在量測修正得當的前提下,卡爾曼濾波值可以平滑準確的估計出目標狀態變量。
(2)由脫靶量可以看出,制導系統中加入濾波后擴展比例導引比純比例導引脫靶量顯著減小,可以大大改進制導系統的精確度,濾除噪聲增加系統的穩定性。
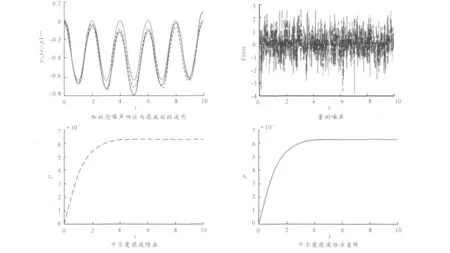
圖2 減小采樣時間后的濾波圖形
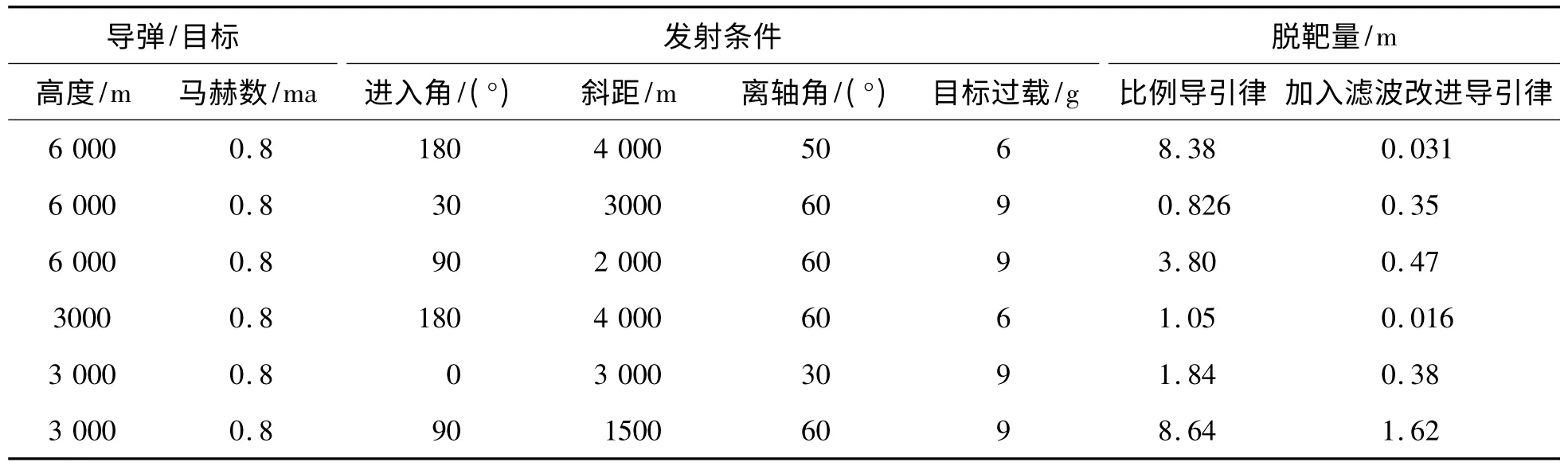
表1 不同仿真條件下兩種制導律的脫靶量對比情況
[1]于翔川.基于非線性濾波的目標跟蹤算法研究[D].西安:西安電子科技大學,2009.
[2]鄭佳興.卡爾曼濾波技術在捷聯姿態測量系統中的應用研究[D].長沙:國防科學技術大學,2007.
[3]周荻.尋的導彈新型導引規律[M].北京:國防工業出版社,2002.
[4]周荻,胡振坤,胡恒章.自適應推廣KALMAN 濾波應用于導彈的被動制導問題[J].宇航學報,1997,184(4):31-36.
[5]王劍,吳嗣亮,房秉毅.基于擴展Kalman 濾波的運動目標距離/速度聯合估計[J].系統工程與電子技術,2007,29(7):1053-1050.
[6]謝春思,王敏慶,董受全,等.基于卡爾曼濾波的反艦導彈火控數據處理[J]. 火力與指揮控制,2009(5):95-97.

