基于時頻分布迭代的跳頻信號參數(shù)估計(jì)?

郭建濤，劉右安

（1.信陽師范學(xué)院物理電子工程學(xué)院，河南信陽464000；2.信陽供電公司，河南信陽464000）

基于時頻分布迭代的跳頻信號參數(shù)估計(jì)?

郭建濤1，劉右安2

（1.信陽師范學(xué)院物理電子工程學(xué)院，河南信陽464000；2.信陽供電公司，河南信陽464000）

提出了一種基于時頻分布迭代的跳頻信號參數(shù)估計(jì)新算法，利用時頻平面最大值，通過計(jì)算跳頻信號與最優(yōu)原子時頻分布的殘差逐次迭代獲取匹配于跳頻信號分量的時頻參數(shù)，進(jìn)而實(shí)現(xiàn)跳頻信號參數(shù)估計(jì)。理論分析和仿真結(jié)果表明，與基于匹配追蹤和粒子群優(yōu)化的跳頻信號參數(shù)估計(jì)相比，基于時頻分布迭代的參數(shù)估計(jì)算法在保證算法精度的情況下，有效地降低了算法的計(jì)算復(fù)雜度，為跳頻信號盲接收的實(shí)時實(shí)現(xiàn)提供了一種新方法。

跳頻信號；參數(shù)估計(jì)；時頻分布；匹配追蹤

1 引言

跳頻通信系統(tǒng)具有良好的抗干擾、低截獲和靈活的組網(wǎng)能力，采用跳頻技術(shù)的各類收發(fā)信機(jī)在軍事通信中得到了廣泛的應(yīng)用；同時，隨著跳頻技術(shù)出現(xiàn)寬帶、高速跳頻以及混合跳頻制式的特點(diǎn)，向通信對抗提出了嚴(yán)峻的挑戰(zhàn)。開展跳頻信號參數(shù)盲估計(jì)技術(shù)的研究，對于當(dāng)前通信對抗和無線電頻譜監(jiān)控等具有重要的理論研究和實(shí)際意義。

跳頻信號屬于典型的非平穩(wěn)信號，傳統(tǒng)的傅里葉變換無法同時給出信號的時間和頻率特性，對該類信號的參數(shù)盲估計(jì)必須使用時頻分析。時頻分析方法又可以分為兩大類。一類是基于時頻圖分析。首先需要通過時頻分析工具獲取跳頻信號的清晰時頻圖，然后根據(jù)其時頻數(shù)據(jù)去估計(jì)跳頻信號的跳周期、跳時和載頻參數(shù)［1-3］。文獻(xiàn)［2］運(yùn)用SPWVD估計(jì)跳頻信號的參數(shù)，該方法在基于時頻圖進(jìn)行參數(shù)估計(jì)時，跳頻周期的準(zhǔn)確性對跳變時刻和跳頻頻率的估計(jì)影響較大，存在誤差累積現(xiàn)象。第二類是基于原子參數(shù)的時頻分析。在給過完備原子庫的基礎(chǔ)上，通過匹配追蹤（Matching Pursuit，MP）算法，由匹配于信號時頻結(jié)構(gòu)的最佳原子直接給出跳頻信號的分能量參數(shù)［4-7］。該類方法由于原子與跳頻信號分量之間的差異，殘差信號能量衰減較慢，使得迭代次數(shù)，即獲取的原子總數(shù)與實(shí)際的跳頻信號分量總數(shù)差別較大，不僅使算法運(yùn)算量顯著增加，而且造成跳頻分量參數(shù)無從選擇。

針對上述兩種方法的優(yōu)缺點(diǎn)，本文在參考匹配追蹤算法基本思想的基礎(chǔ)上，提出新的適應(yīng)度函數(shù)對信號進(jìn)行稀疏分解，仿真結(jié)果驗(yàn)證了本文算法的有效性。

2 問題描述

跳頻信號是一類載頻在偽隨機(jī)序列控制下隨時間變化的非平穩(wěn)信號，可以表示為

式中，T為觀測時間，n（t）為高斯白噪聲，S為信號功率，rectTH（t）為寬度為TH的矩形窗。

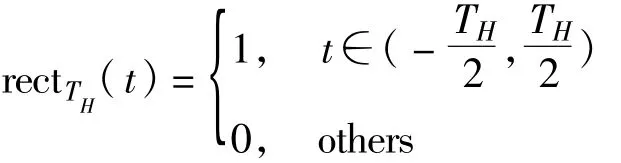
式中，TH為跳頻周期，fk為第k跳的中心頻率，第k跳的跳變時刻為αTH+（k-1）Th。

上述跳頻信號可以看作多個具有不同時頻中心的單音頻信號的疊加，這里稱為跳頻分量。令tk表示第k個跳頻分量的時間中心，dk表示其時間駐留長度。只要依據(jù)一定的算法求出分量的時頻中心（tk，fk），就能根據(jù)相應(yīng)的對應(yīng)關(guān)系估計(jì)出跳頻信號的所有參數(shù)，因此跳頻信號的參數(shù)估計(jì)問題就轉(zhuǎn)化為跳頻信號有效分量的選取。

3 標(biāo)準(zhǔn)匹配追蹤算法的瓶頸

3.1 匹配追蹤算法的基本原理

MP算法是利用信號在極度冗余的原子庫中時頻原子上的正交投影來逐次近似。假設(shè)原子庫為

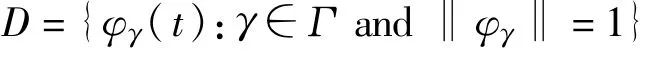
其中，D∈RN×M，N表示信號長度，且滿足M＞＞N；φγ表示基本原子，Γ表示原子參數(shù)集。

設(shè)置初始輸入信號為當(dāng)前殘差信號，即令x0（t）=x（t）。首先按照與x（t）的內(nèi)積最大的原則挑選出與信號x（t）最匹配的時頻原子φγ0，將x（t）分解為

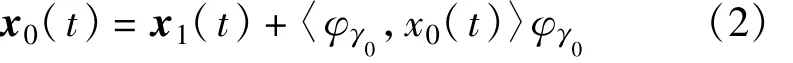
式中，〈·〉表示兩個向量的內(nèi)積，x1（t）是經(jīng)過一步迭代后的殘差信號。

然后，按公式（3）和公式（4）迭代分解，得到第n步的殘差xn（t）：

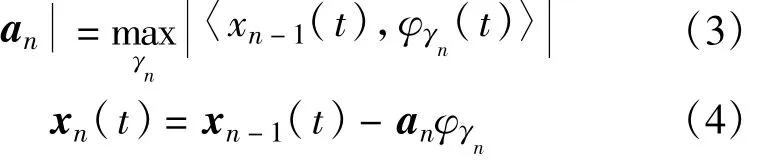
式中，max 表示求參數(shù)集中的內(nèi)積最大值，·表示求模運(yùn)算。

最后，經(jīng)過m步迭代后，可以得到信號的m步近似結(jié)果：

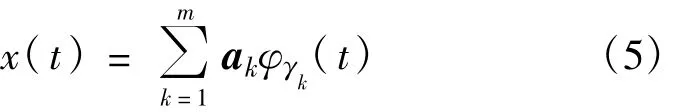
其中，m可以由殘差信號的變化量或者預(yù)先設(shè)置的最大迭代次數(shù)決定。

3.2 原子庫的降維處理

MP算法成功應(yīng)用的關(guān)鍵因素之一是原子庫的冗余性，因?yàn)橹挥袠?gòu)建一個超完備的原子庫，算法才能在庫中搜索到與信號時頻結(jié)構(gòu)相一致的原子，否則由于原子參數(shù)誤差的存在，造成算法收斂減慢，并且出現(xiàn)較多的偽分量［5］。出于跳頻信號參數(shù)估計(jì)的目的，在忽略跳頻信號分量相位信息的基礎(chǔ)上，每一個跳頻周期內(nèi)的信號可以由其時間駐留長度、駐留時間、時頻中心3個參數(shù)唯一確定，因此應(yīng)用標(biāo)準(zhǔn)匹配追蹤算法進(jìn)行跳頻信號分量獲取時，至少需要構(gòu)建參數(shù)向量為γi=｛ti，fi，di｝的三維原子庫。但是，當(dāng)原子庫維數(shù)增加時，由于算法通過搜索整個原子庫的內(nèi)積來確定參數(shù)，其計(jì)算量非常巨大。例如，假設(shè)每個參數(shù)離散化成1 000個點(diǎn)，原子庫原子數(shù)目就是109，搜索原子的每一步迭代都需要計(jì)算信號與所有原子的內(nèi)積計(jì)算，其計(jì)算代價幾乎無法承受；另外，原子庫的存儲也對計(jì)算機(jī)的存儲帶來巨大的挑戰(zhàn)。為了克服上述缺點(diǎn)，本文首先對信號進(jìn)行時頻分析，計(jì)算信號的時頻分布，利用已有的時頻分布在時頻平面上搜索原子的時頻中心，確定原子的前兩個參數(shù)（tk，fk）；最后，在一維尺度空間內(nèi)搜索跳頻信號分量的駐留時間參數(shù)。

假設(shè)選用具有單位能量的加窗正弦函數(shù)作為時頻原子，即

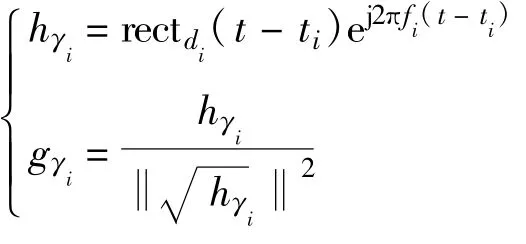
式中，（tk，fk）由每一步迭代對應(yīng)的時頻分布最大值確定，參數(shù)di在原子庫中搜索與信號內(nèi)積最大值獲取。由此可見，原子庫搜索空間由三維降低為一維。

進(jìn)一步地，對于跳頻周期為常數(shù)的跳頻信號，除了首尾兩個跳頻信號分量，其時間駐留長度相等，即di=TH。

因此，可以由MP算法搜索到的d1作為其他原子的尺度參數(shù)，這也避免了數(shù)據(jù)在后續(xù)迭代過程中殘差信號造成的參數(shù)di估計(jì)誤差。

4 參數(shù)估計(jì)算法

算法在計(jì)算時頻分布的基礎(chǔ)上，通過時頻平面上最大值獲取最優(yōu)原子，以迭代的方法逐個獲取與跳頻信號時頻分量相匹配的原子參數(shù)，進(jìn)而估計(jì)跳頻信號參數(shù)，其算法框圖如圖1所示。

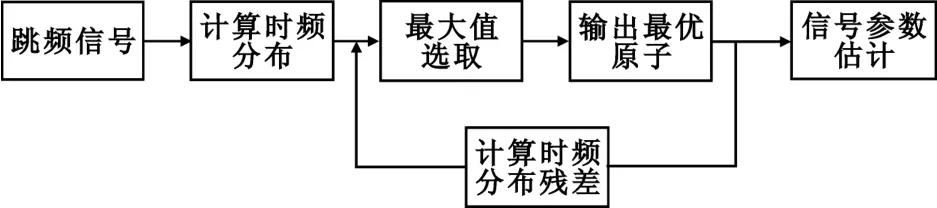
圖1 算法流程圖示Fig.1 Flowchart of FH signals estimation algorithm

采用平滑偽魏格納分布的跳頻信號參數(shù)估計(jì)的具體算法步驟如下。

（1）對接收到的跳頻信號x（t）進(jìn)行歸一化，計(jì)算其平滑偽魏格納分布Wn（t，f）（此時n=1），獲取第一個原子的時頻中心參數(shù)。

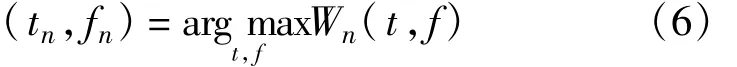
（2）固定原子的時頻中心，搜索時頻原子的尺度參數(shù)d1。

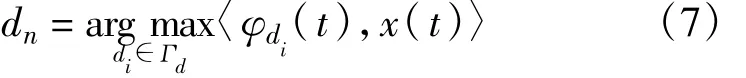
式中，Γd表示尺度參數(shù)集。并以d1作為后續(xù)選取原子的時間支撐。

（3）計(jì)算三參數(shù)γn=｛tn，fn，d1｝原子的時頻分布W′n（t，f），并修正跳頻信號的時頻分布：

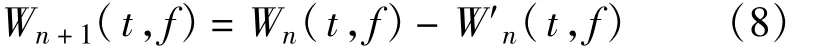
（4）重復(fù)步驟1和步驟3，求取后續(xù)原子的時頻中心參數(shù)（tn，fn），直到算法達(dá)到最大迭代次數(shù)為止。

（5）將原子的時間參數(shù)按照先后順序排列，找到發(fā)生在中間的n-2個原子，對時間中心差分后求平均值，得到跳頻周期的估計(jì)值＾TH。

（6）由最小時間中心參數(shù)tn和T＾H，可以得到跳頻信號分量的跳變時刻，即；跳頻頻率就是tn-原子的頻率參數(shù)。

5 仿真與分析

設(shè)定觀測時間為8個跳頻周期，采樣得到256個樣本值，其跳頻頻率fk依次為｛5，45，20，10，35，15，25，40，5｝Hz，采樣率為fs=100 Hz，跳周期TH= 0.32 s，跳變時刻αTH=TH／2。

圖2給出了跳頻信號經(jīng)時頻分布迭代追蹤后獲取的原子時頻分布之和。為了對比，圖3給出了文獻(xiàn)［8］采用匹配追蹤和粒子群優(yōu)化結(jié)合的MSPSO算法得到的跳頻信號時頻表示。可以看到，圖2給出了跳頻信號的清晰時頻分布，直觀地顯示了跳頻信號載波頻率隨時間變化的曲線。圖3中分量的時頻表示在時間和頻率支撐上都與實(shí)際值有所差異，同時有分量丟失現(xiàn)象。為了進(jìn)一步求出跳頻信號參數(shù)，通過對算法選取6個原子的時頻參數(shù)值與其真值進(jìn)行的比較表明，時間中心參數(shù)的最大誤差是0.02 s，而頻率參數(shù)在取整后與載波頻率值完全相同。

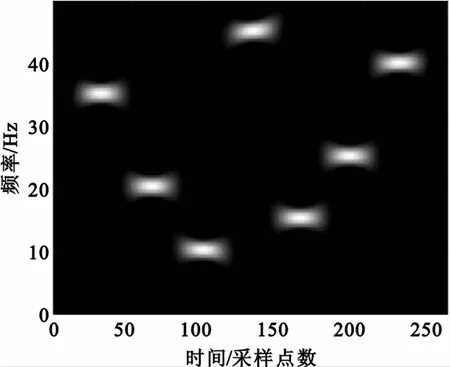
圖2 原子組合時頻分布Fig.2 Time frequency representation combined by atoms

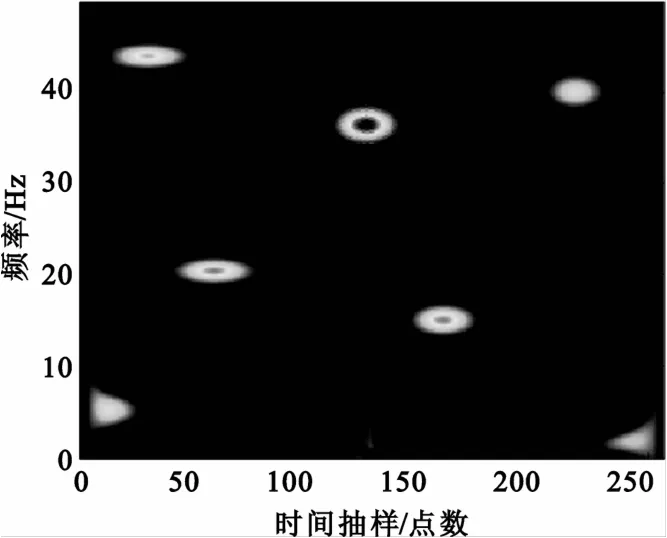
圖3 基于MSPSO算法的時頻表示Fig.3 Time frequency representation using MSPSO

最后，與匹配追蹤算法基于過完備原子庫最優(yōu)原子搜索不同，提出的參數(shù)估計(jì)算法是在時頻平面上通過極大值搜索選取最優(yōu)原子。在計(jì)算原始跳頻信號時頻分布的基礎(chǔ)上，后續(xù)時頻分布的計(jì)算是針對最優(yōu)原子，算法的運(yùn)算量低于匹配追蹤算法中粒子群的適應(yīng)度函數(shù)計(jì)算量。實(shí)驗(yàn)結(jié)果表明，在相同迭代次數(shù)（與跳頻信號分量數(shù)相當(dāng)）的情況下，文獻(xiàn)［8］的運(yùn)算時間是29.546 9 s（采用粒子群算法參數(shù)：群規(guī)模50，迭代50次），而本文算法運(yùn)算時間是2 s。

6 結(jié)論

跳頻信號參數(shù)盲估計(jì)是實(shí)現(xiàn)跳頻信號截獲、干擾和頻譜監(jiān)控的前提和基礎(chǔ)，研究跳頻信號參數(shù)盲估計(jì)的快速算法是一項(xiàng)非常有意義的課題。目前跳頻信號基于匹配追蹤算法的自適應(yīng)分解技術(shù)存在運(yùn)算量過大和分量個數(shù)難以確定的瓶頸。本文利用跳頻信號時頻平面最大值，通過計(jì)算跳頻信號與最優(yōu)原子的時頻分布?xì)埐顚?shí)現(xiàn)跳頻信號分量的逐次獲取，將三維空間搜索轉(zhuǎn)化到一維空間內(nèi)，降低了算法的計(jì)算復(fù)雜度，提供了實(shí)際應(yīng)用中的一條有效途徑。

［1］Barbarossa S.Parameter estimation of spread spectrum frequency hopping signals using time-frequency distributions［C］／／Proceedings of Signal Processing Workshop on Signal Processing Advances in Wireless Communications.Paris，F(xiàn)rance：IEEE，1997：213-216.

［2］趙俊，張朝陽，賴?yán)澹?一種基于時頻分析的跳頻信號參數(shù)盲估計(jì)方法［J］.電路與系統(tǒng)學(xué)報，2003，8（3）：46-50. ZHAO Jun，ZHANG Zhao-yang，LAILi-feng，et al.Blind Parameter Estimation of Frequency-Hopping Signals Based on Time-Frequency Analysis［J］.Journal of Circuits and Systems，2003，8（3）：46-50.（in Chinese）

［3］張曦，杜興民.基于短時哈特萊變換的跳頻信號時頻分析［J］.信號處理，2007，23（2）：192-194. ZHANG Xi，DU Xing-min.Time-Frequency Analysis of Frequency-Hopping Signals Based on Short-time Hartley Transform［J］.Signal Processing，2007，23（2）：192-194.（in Chinese）

［4］郭建濤.幾種跳頻信號時頻表示的熵測度研究［J］.微計(jì)算機(jī)信息，2008，24（33）：103-106. GUO Jian-tao.A comparative study of some time-frequency representations of frequency-hopping Signal using Renyi criterion［J］.Microcomputer Information，2008，24（33）：103 -106.（in Chinese）

［5］王建英，尹忠科，張春梅，等.信號與圖像的稀疏分解及初步應(yīng)用［M］.成都：西南交通大學(xué)出版社，2006. WANG Jian-ying，YIN Ke-zhong，ZHANG Chun-mei，et al.Sparse Decomposition of Signal and Imaging and Preliminary Application［M］.Chengdu：Southwest Jiaotong University Press，2006.（in Chinese）

［6］Lopez G，Ojeda O Y.Atomic decomposition based complex radar interception［C］／／Proceedings of Radar，Sonar and Navigation.Salt Lake City，USA：IEEE，2006：323-331.

［7］Guo Jiantao.Adaptive time-frequency parameterization of frequency-hopping signals based on evolutionary algorithm［C］／／Proceedings of the third International Joint Conference on Computer Science and Optimization.Anhui，China：IEEE，2010：279-282.

［8］郭建濤，王宏遠(yuǎn)，余本海.基于粒子群算法的跳頻信號參數(shù)估計(jì)［J］.計(jì)算機(jī)應(yīng)用研究，2010，27（2）：512-514. GUO Jian-tao，WANG Hong-yuan，YU Ben-hai.Parameter estimation of frequency hopping signal based on particle swarm optimization［J］.Application Research of Computers，2010，27（2）：512-514.（in Chinese）

Parameter Estimation of Frequency Hopping Signals Based on Time Frequency Distribution Iteration

GUO Jian-tao1，LIU You-an2
（1.College of Physics and Electronic Engineering，Xinyang Normal University，Xinyang 464000，China；2.Xinyang Power Supply Company，Xinyang 464000，China）

A new parameter estimation algorithm for frequency hopping（FH）signal based on time frequency（TF）distribution iteration is proposed.The TF parametersmatching those components of FH signals are obtained successively by residual computation of TF distribution between FH signal and the best atom using the TF plane maximum values.Further，the FH parameters are estimated.Theoretical analysis and simulation results show that this algorithm reduces the computational complexity effectively under the circumstance of ensuring the estimation accuracy and provides a new way to receive FH signal real-timely and blindly.

frequency hopping signal；parameter estimation；time frequency distribution；matching pursuit

The Natural Science Foundation of Henan Province Educational Committee（2011A510021）；High-level Talent Scientific Research to Start Fund Projects of Xinyang Normal University（No.09217）

the M.S.degree from Dalian University of Science and Technology and the Ph.D.degree from Huazhong University of Science and Technology in 2004 and 2009，respectively.He is now an associate professor.His research interests include communications signal processing and time frequency analysis.

1001-893X（2012）04-0514-04

2011-12-01；

2012-02-17

河南省教育廳自然科學(xué)基金資助項(xiàng)目（2011A510021）；信陽師范學(xué)院高層次人才科研基金項(xiàng)目（09217）

TN929.5

A

10.3969／j.issn.1001-893x.2012.04.018

郭建濤（1973—），男，河南南陽人，2004年于大連理工大學(xué)獲碩士學(xué)位，2009年于華中科技大學(xué)電子與信息工程系獲通信與信息工程專業(yè)工學(xué)博士學(xué)位，現(xiàn)為副教授，主要研究方向?yàn)橥ㄐ判盘柼幚砗蜁r頻分析技術(shù)。

Email：e-jiantao＠163.com

GUO Jian-tao was born in Nanyang，Henan Province，in 1973.He