商用數碼相機透鏡畸變校正算法比較

李芳芳，劉華朋

(1.西南交通大學希望學院，四川南充 637900，2.中鐵十六局集團路橋工程有限公司，北京 101500)

為實現工程測量與數字近景攝影測量的結合，量測型數碼相機應運產生。但量測數碼相機價格昂貴，所以宜采用商用的數碼相機。即商用量測型數碼相機，但其相機的內方位元素(X0，Y0，f)未知，且其鏡頭畸變對測量的精度影響較大，因此在進行高精度的測量模式作業前需要對相機進行嚴格的標定［1］。

攝像機的標定是確定攝像機內部參數或外部參數的過程。內部參數是指攝像機內部的幾何和光學特性，外參數是指攝像機相對世界坐標系原點的平移和旋轉位置。

在檢測的視覺系統中，使用廣角鏡頭可以進行大范圍測量［2］，但短焦距、廣角鏡頭的攝像機系統與理想的小孔透視模型(pin hole model)有一定的差別，從而使得物體點在攝像機圖像平面上實際所成的像與理想成像之間存在不同程度的非線性光學畸變［5］。相機鏡頭的非線性畸變僅與它所選用的焦距有關，與其他的內部參數、外部參數無關?；儓D像不利于計算機視覺進行現場測量和圖像處理，必須對圖像的非線性畸變進行校正，校正精度直接影響到最終的測量精度。

圖像的非線性畸變主要分為兩部分:徑向畸變和切向畸變。切向畸變較小，影響不大，一般不予考慮，以徑向畸變為主。如能預先知道畸變模型，則進行校正后就可應用針孔攝像機模型來進行視覺計算。然而制造商一般不提供鏡頭的畸變模型，并且批量生產中不可避免的隨機性導致同一規格型號鏡頭的畸變參數也不相同，這就需要有簡便的方法來獲取鏡頭的畸變參數。

1 數碼圖像的非線性畸變

圖像的非線性畸變與相機成像過程中的外部參數和光源到鏡頭的距離無關，僅與光線經過鏡頭的位置有關?；兊男纬墒怯捎谌肷涔饩€在通過各個透鏡時的折射誤差和電荷耦合器件(Charge Couple Device，CCD)點陣位置誤差所致。不同的焦距將對應著不同的非線性畸變，因為調焦將引起主點位置(x0，y0)的變化，所以在獲取照片的時候要鎖定主距，以達到鎖定內方位元素值和光學透鏡畸變系數的目的［4］。

對一架變焦相機來說，它的非線性畸變特性是隨著焦距的變化而變化，選定一種焦距，也就有一個確定的畸變與之對應;定焦相機的非線性畸變特性是固定的。隨著CCD 制造技術的發展，CCD 的像素值越來越大，像素點間距也變得越來越小，圖像中的非線性畸變在機器視覺的研究中就顯得更為重要。非線性畸變的研究成為很多學者研究的內容。姜大志等人［1］提出了把非線性畸變參數的求解獨立于相機其他參數求解的方案，可以獲得較高精度的畸變參數，為機器視覺技術的應用提供了一種簡捷、可靠、實用的新方法，但這要利用專門的實驗室裝置在實驗室中進行。張靖等人［2］采用基于直線的射影變換特點，提出一種校正鏡頭畸變的非量測算法，用面積平方和定義畸變測度，計算量小且具有抗噪聲能力，避免了收斂于局部極小值，但方法復雜;朱漢敏［3］利用畸變的球形模型，基于物方直線特征，實現了畸變的數字校正，整個校正過程不需要其他的光學測量儀器，也不需要知道光學系統的結構參數，只是根據畸變特征進行校正。

在圖像坐標系中的非線性畸變包括徑向畸變、離心畸變、薄棱鏡畸變。若同時考慮這三部分的影響，將因為引入過多的非線性畸變參數而引起解的不穩定［10］。田原嫄以理想針孔成像模型為基礎，證明了影響畸變的主要因子是徑向畸變，其他因子的影響基本不大，可忽略不計［5］，因此在一般應用中僅考慮徑向畸變。徑向誤差是由鏡頭中各組透鏡的表面曲率存在誤差引起的，在以徑向畸變為主的非線性幾何畸變模型中，無畸變像面坐標和畸變像面坐標之間的關系可表示為:

式中:xp、yp為無畸變像平面坐標;xd、yd為畸變像平面坐標，它們的坐標原點都在對稱中心;k為徑向畸變系數，k＞0 表示枕形畸變，k＜0 表示桶形畸變。

通過對徑向畸變校正算法的研究回顧，發現球形模型算法和多項式算法是運用較多的兩個算法，且精度也達到了各自所研究對象的徑向畸變校正的要求。為探索哪一種算法滿足更高校正精度要求，本文以實驗比較這兩種算法的精度。

2 實驗校正過程

實驗使用的相機焦距可調，拍照時采取手動調焦來固定焦距，以得到準確的焦距參數。本實驗采用的焦距參數為5.8 mm。

繪制一個等間隔正交方網格，由25 根橫向直線和25 根縱向直線組成，縱、橫向直線間的距離為5 mm，線長度誤差小于7‰，線寬0.07 mm。在相機拍攝時，方格網應能布滿成像平面，且使光軸垂直于方格網，光軸盡量通過方格網中心，因此需要一個便于調節的相機支撐裝置。

將繪好的正交方格網貼附于平面上，用待校相機照準成像，獲得如圖1 所示的原始圖像。從圖可看出網格邊沿處明顯有畸變，實際存在的物方直線在影像上是一條曲線。

2.1 球形模型校正法

物方一直線段在徑向畸變下變為橢圓的一段，橢圓弧可視為標準橢圓中心平移到C(x0，y0)、旋轉θ0而得，橢圓的長半軸a 等于球形模型的半徑R。文獻［5］證明用球形模型表示徑向畸變是恰當的，任意一點的位置畸變僅與該點極坐標中的矢徑坐標有關，在球形模型下，極坐標公式為:

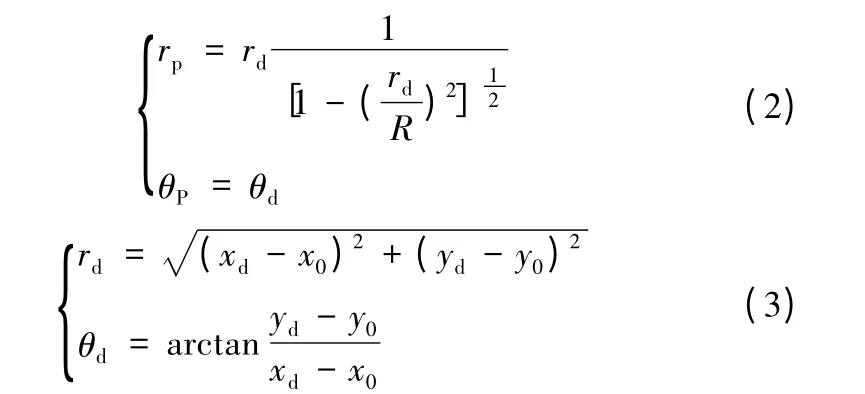
式中:rp、θp為無畸變點的極徑和極角;rd、θd畸變點的極徑和極角;R為球半徑;x0、y0為畸變中心;xp、yp、xd、yd的涵義同式(1)。

校正過程是先對原始圖像進行二值化處理和骨架提取，處理出網格交點，獲得交點處的數字坐標，然后根據標準特征值分解(Eigen Value Decomposition，EVD)算法和徑向畸變下的橢圓弧方程［10］，可求得R 和(x0，y0)。這樣就可以根據畸變圖像中各點的坐標(xd，yd)算得對應的無畸變點(rp，θp)，從而校正圖像。

原圖像像素點變換后坐標一般要改變，若沒落在像素點上，此時可用相鄰像素點上的灰度值通過插值求出其灰度值，常用的插值算法有最鄰近點法、雙線性內插法及三次卷積法;最鄰近點法算法非常簡單并且保持原光譜信息不變，但是幾何精度較差;雙線性插值法具有計算簡單、幾何上準確度較高、能克服灰度不連續等優點;三次卷積法計算量較大，但比較準確。綜合考慮各個算法的優缺點，實驗采用雙線性內插法進行插值，經過插值后，可避免校正后圖像出現“空”像素的情況。

圖2 是糾正了透鏡畸變的方格網，從圖上可以看出，網格線已全部拉直。

2.2 多項式糾正法

多項式表示的徑向畸變模型公式為:

圖1 待校正畸變圖

圖2 球形模型校正結果

式中:aij為多項式的系數;n為多項式的次數。

透鏡的徑向畸變有均勻畸變和不均勻畸變。曾巒［8］采用的透鏡畸變是均勻畸變，校正結果較理想。均勻畸變是不均勻畸變的特殊情況，為了不失一般性，假定實驗的透鏡畸變為不均勻畸變。在方格網成像后，因為透鏡畸變的存在，每一交點的坐標為實際成像坐標。

針對圖1 所示的原始圖像進行計算，先對該圖像進行二值化處理和骨架提取，處理出網格交點，并分別讀出各交點的實際成像坐標。視線上的所有物點都成像在像面上同一位置，利用這一特性可以讓原方格網的中心和成像后的方格網的成像中心在同一個位置，這樣實際成像坐標所對應的理想成像坐標也是知道的，則可以得到每一交點處的徑向畸變系數，利用該點的畸變系數及式(4)對圖像進行校正，生成的無畸變圖像如圖3 所示。需要說明的是用多項式法校正和球形模型法校正一樣，也需要進行灰度內插。

統計糾正前后網格點(角點)像素坐標的變化可說明圖像糾正的精度。原始圖像是等間隔正交方網格，像素坐標系的原點在CCD 圖像平面的左上角，I 軸、J 軸分別平行于圖像坐標系的x 軸和y 軸。在進行殘差統計時，使用中誤差、平均誤差及畸變最大值等統計量，統計結果如表1 所示。

圖3 多項式校正結果

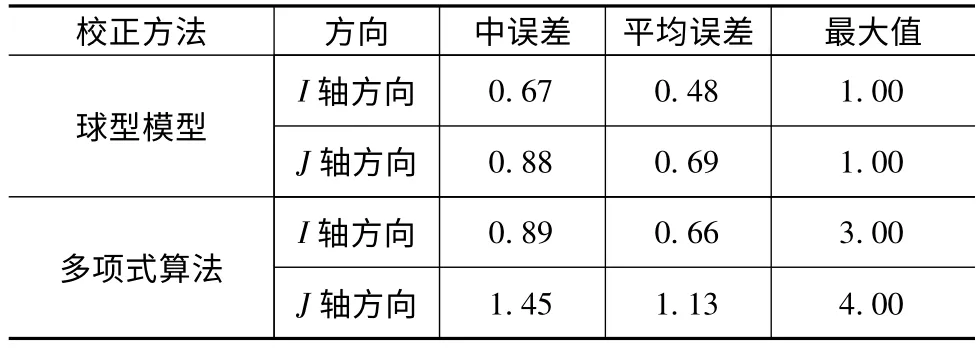
表1 圖像校正后格網角點像素坐標與標準像素坐標的殘差統計結果(像素)

從表1可以看出，無論是I 軸方向還是J 軸方向，球形模型校正的誤差均小于多項式算法校正的誤差。還可以看出，無論是球形模型校正還是多項式算法校正，縱向(J 軸)的誤差均大于橫向(I 軸)的誤差，這是因為縱向為相機拍攝方向，照片產生幾何變形主要是由縱向失真引起。因本論文圖像的像素間距為0.064 mm，可知球型模型校正的I 軸方向中誤差為0.04 mm，平均誤差為0.03 mm，最大誤差為0.064 mm，J 軸方向中誤差為0.06 mm，平均誤差為0.05 mm，最大誤差為0.064 mm。

3 結 論

采用球形模型和多項式兩種算法對數碼影像進行畸變校正處理，校正結果無論從直觀上還是量化數據上，都可以得出球形模型的校正精度比多項式校正精度高。除此之外，球形模型校正算法簡單，實用性也好，可以得出球型模型校正的精度可以滿足更高畸變校正要求的結論。

［1］姜大志.標準圖形法求解相機鏡頭非線性畸變的研究［J］.東南大學學報，2001，31(4)

［2］張靖.攝像機鏡頭畸變的一種非量測校正方法［J］.光學學報，2008，28(8)

［3］朱漢敏.基于直線特征的徑向畸變圖像的校正［J］.上海工程技術大學學報，2006，20(2):154－155

［4［ 崔紅霞.非量測數碼相機的畸變差檢測研究［J］.測繪科學，2005，30(1)

［5］田原嫄.基于CCD 攝像機成像的徑向畸變研究［J］.世界科技研究與發展，2008，30(2)

［6］Tsai R Y.A versatile camera calibration technique for high－accuracy 3D machine vision［J］.International Journal of Robotics and Automation，1987，3(4):323－344

［7］馮文灝.數碼相機實施攝影測量的幾個問題［J］.測繪信息與工程，2002，27(3)

［8］曾巒.短焦距攝像機鏡頭的畸變校正方法［J］.裝備指揮技術學院學報，2002，13(2):53－55

［9］鄭瑩.鐵路軌道數碼影像的糾正與拼接［D］.西南交通大學，2008

［10］田涌濤.基于共線點的透鏡畸變系數標定［J］.上海交通大學學報，2003，37(11)