自適應步長加權正交約束自然梯度ICA算法

唐興佳，張秀方

(西安電子科技大學理學院，陜西 西安 710071)

在傳輸通道未知情況下，從觀測信號中恢復統計獨立的源信號，稱為盲信號分離(Base Station Subsystem，BSS)［1］。作為當前信號處理領域研究的熱點課題之一，BSS已經在地震勘探、移動通信、語音處理、列陣信號處理及生物醫學工程等領域得到廣泛應用。

獨立分量分析(ICA)［2］起源于BSS中的雞尾酒會問題，即在多個人的說話聲相互混疊的情況下，將各個人的語音單獨分離出來。ICA算法主要分為批處理算法和自適應算法兩類。批處理算法，如FastICA算法［2］、聯合對角化算法［2］等，數值穩定性較好，但不適于觀測數據即時更新的系統。自適應算法，如EASI算法［3］、自然梯度 ICA 算法［1］等，計算量較小，且具有在線學習能力，但算法的收斂性和穩定性受學習步長的影響較大。

ICA的核心是通過恢復信號之間的統計獨立性，實現信號分離，而信號之間統計獨立一定線性不相關。在ICA的基本假設下，限定分離矩陣的正交性約束，等價于分離信號為白化信號。傳統的自然梯度IAC算法沒有注意到分離信號的這一假設要求，使得分離矩陣的迭代過程不穩定，最終導致恢復的源信號不準確。

為提高算法的穩定性、收斂性以及分離結果的準確性，文中基于自然梯度ICA算法，改進提出一種自適應調整步長的加權正交約束自然梯度ICA算法，然后通過實驗仿真驗證新算法的優越性。

1 問題描述

在ICA模型中，觀測信號來自一組傳感器的輸出，每個傳感器接收到的都是多個源信號的混合。n個信號源發出的源信號st=(s1(t)，s2(t)，…，sn(t))T通過傳輸通道被m個傳感器接收，得到觀測信號xt=(x1(t)，x2(t)，…，xm(t))T。在無噪聲條件下，ICA 瞬時混合模型可表示為［2］

其中，A為混合矩陣。假設A具有足夠的非奇異性，則源信號也可看作觀測信號的線性組合。這樣，求解ICA問題就是要確定一個矩陣W，稱為分離矩陣，使得矩陣變換結果

可作為源信號 st的估計［2］，稱 yt=(y1(t)，y2(t)，…，yn(t))T為分離信號。

上述模型的基本假設是［2］:(1)源信號的各個分量相互獨立，且最多只有一個分量服從高斯分布;(2)源信號的各個分量具有零均值和單位方差。還需注意的是，在ICA模型中，分離信號相比于源信號會出現順序和幅度上的不確定性。但由于ICA的主要目的是把源信號分離出來，對分離信號的順序并沒有要求，而幅度的不確定，只需在分離信號前乘以一個適當的系數即可消除，因而，ICA的這兩種不確定性對最終結果的影響并不大。

2 自然梯度ICA算法

對于ICA模型，源信號無法被直接觀測，且混合矩陣A未知，但源信號的各個分量相互獨立是已知的。前文已經指出，ICA的關鍵就是根據源信號之間的統計獨立性，尋找觀測信號x的某個特殊的矩陣變換y=Wx，使得變換后的每個分量都能表示一個不同的源信號。因此，求解ICA模型，首先要對分離結果Wx的獨立性做出度量，然后將該度量函數作為目標函數，借助梯度下降等優化方法，即可找到問題的解。

文中基于似然度［2］構造獨立性度量函數，并得到自然梯度 ICA的在線學習規則［4－7］為

其中，G(y)為分值函數;η(t)為學習步長。通常情況下，由于源信號的概率密度函數未知，因而，分值函數也是未知的。實際應用中，常用某個適當的單調奇函數作為激勵函數來代替分值函數，例如G(y)=y3。

3 加權正交約束的考慮

由ICA模型的基本假設可知，源信號s具有單位方差，則恢復的分離信號y也應具有單位方差，即E{yyT}=I。假設觀測數據是白化的，即有E{xxT}=Rx= δ2I，于是

式(4)表明，在恢復的源信號y和觀測信號x均為單位方差的情況下，分離矩陣W應是對稱正交的［1］。但是，觀測數據x為單位方差不一定總滿足。這樣，分離矩陣的對稱正交性就是不合實際的。因此，需要考慮加權正交約束WRxWT=I。

綜上所述，在不進行觀測數據的預白化時，可通過對傳統的自然梯度ICA算法引入加權正交約束WRxWT=I，便可達到白化效果［8－9］。文中提出一種近似處理，在自然梯度ICA算法的每步迭代后，對分離矩陣W進行單步正交性修正

4 自適應步長的考慮

在自然梯度ICA算法中，學習步長η的選擇對算法的收斂起著關鍵作用。η越大，收斂速度越快，但收斂后的穩態誤差也就越大;η越小，收斂速度越慢，同樣會影響到算法的性能。而好的學習步長選擇與分離結果和最優值的距離有關。當分離結果y遠離其最優值時，應增大η的取值，以加快收斂速度;當分離結果y處于其最優值附近時，應減小η的取值，以減小算法的穩態誤差。而且，為保證算法的穩定收斂，還要限制η的取值范圍［10－12］。一種簡單的方法是將學習步長定義為迭代次數的反比例函數或者指數下降函數，但在時變環境下，這種方法的跟蹤搜索能力并沒有得到根本改善。

自適應調整步長就是依據上述分析提出的，特別在時變環境中，不但能保證算法收斂速度足夠快，而且能提高算法的穩定性。在ICA模型中，不可能事先得到模型的最優解，也就不可能用實際誤差來控制學習步長。因此，文中通過引入誤差估計函數，提出一種自適應調整的步長。

由式(3)可知，當算法收斂時，分離矩陣的相鄰迭代之差W(t)－W(t－1)≈0，換個角度考慮，就是要求η(t)(I－G(y(t))(y(t))T)W(t－1)≈0。這樣，可以用式(8)構造誤差估計

考慮到延遲誤差對學習步長選擇的影響，這里取H(t)的平滑形式［13］

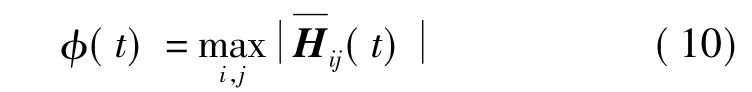
由于步長的選擇與前一步迭代時的步長及當前迭代的誤差估計有關，于是，可以定義自適應步長

其中，β為遺忘因子，一般取接近1的實數，顯然β越大，學習步長的調整幅度越小。為ρ比例因子。為了避免η(t)過大，導致算法不穩定，在此設定η(t)有上限

5 仿真實驗

為檢驗新算法的穩定性、收斂性及分離結果的準確性，取以下信號進行實驗仿真［14］:s1(t):方波信號sign(cos(2π×155t));s2(t):高頻正弦信號sin(2π×800t);s3(t):低頻正弦信號sin(2π×90t);s4(t):相位調制信號 sin(2π×300t+6cos(2π×60t));s5(t):幅度調制信號 sin(2π×10t)sin(2π×300t);s6(t):在［－1，1］上服從均勻分布的噪聲信號。

假設模型使用6個觀測感應器即m=6，n=6;混合矩陣A隨機產生，且服從［－1，1］上的均勻分布;信號的采樣周期Ts=0.0001 s;算法收斂穩定性能用“串音誤差”來衡量［14］

其中，cpq=［W·A］pq稱為混合 －分離系統的傳遞矩陣。

自適應步長加權正交約束自然梯度ICA算法的仿真實驗步驟如下:

(1)隨機產生混合矩陣，對n個源信號進行線性混合，得到m個混合信號。

(2)初始化分離矩陣 W(0)=In×m，協方差矩陣Rx(0)=Im，學習步長 η(0)=0.01，平滑誤差估計0)=In×n。

(3)取遺忘因子β=0.998，比例因子ρ=0.25。

(4)計算y(t)=W(t)x(t)。

(5)更新學習步長η(t)、更新協方差矩陣Rx(t)、更新分離矩陣W(t)。

(6)對分離矩陣W(t)進行單步正交性修正。

(7)計算串音誤差Ect(t)。

(8)如果 t≠T，取 t←t+1，返回步驟(4)，否則，迭代結束。

(9)依據y(t)和Ect(t)繪制恢復的源信號波形和算法性能曲線。

具體仿真結果如圖1～圖4所示。

由圖2和圖3可以看出，自然梯度ICA算法可以對混合信號進行較為有效的分離，但分離結果的準確性明顯不高。相比之下，基于自適應調整步長和加權正交約束的新算法恢復的源信號則要更準確。另外，由圖4可以看出，相比于自然梯度ICA算法，改進的新算法在迭代前期具有更快的收斂速度。同時，自然梯度ICA算法的收斂穩定性曲線，在迭代相對穩定后，一直有較大的跳躍，這就意味著算法不穩定。自適應步長加權正交約束自然梯度ICA算法減弱了這一曲線跳躍，算法更穩定，且穩態誤差更小。由此可得，新算法的收斂性、穩定性及分離結果的準確性較傳統算法得到了一定改善。

6 結束語

傳統的自然梯度ICA算法對分離矩陣的正交性約束未做考慮，且算法的穩定性和收斂性受學習步長的影響較大，因此算法性能較差。文中通過引入加權正交約束和自適應調整步長理論，在傳統算法的基礎上，改進得到一種新的自然梯度ICA算法。仿真實驗表明，自適應步長加權正交約束自然梯度ICA算法相比于傳統的自然梯度ICA算法具有更快的收斂速度，且算法的穩定性和分離結果的準確性都有較大提高。

［1］ANDRZEJ C，SHUN－CHI A.自適應盲信號與圖像處理［M］.吾正國，唐勁松，章林柯，譯.北京:電子工業出版社，2004.

［2］HYVARINEN A，KARHUNEN J，OJA E.Independent component analysis［M］.Newyork:Wiley Press，2001.

［3］CARDOSO J F，LAHELD B.Equivariant adaptive source separation ［J］.IEEE Transactions on Signal Processing，1996，45(2):434 －444.

［4］AMARI S.Natural gradient works efficiently in learning［J］.Neural Computation，1998(10):251 －276.

［5］BELOUCHRANI A，MERAIM K，CARDOSO J F，et al.A blind source separation technique using second－order statistics［J］.IEEE Transactions on Signal Processing，1997，45(2):434－444.

［6］ZHANG W T，LIU N，LOU S T.Joint approximate diagonalization using bilateral rank－reducing householder transform with application in blind source separation ［J］.Chinese Journal of Electronics，2009，18(3):471 －476.

［7］DEGERINE S，KANE E.A comparative study of approximate joint diagonalization algorithms for blind source separation in presence of additive noise［J］.IEEE Transactions on Signal Processing，2007，55(6):3022 －3031.

［8］ZHU Xiaolong，ZHANG Xianda，DING Zizhe，et al.Adaptive nonlinear PCA algorithms for blind source separation without prewhitening［J］.IEEE Transactions on Circuits and Systems，2006，53(3):745 －752.

［9］YE Jimin，HUANG Ting.New Fast－ ICA algorithms for blind source separation without prewhitening［J］.Communications in Computer and Information Science，2011，255(2):579－585.

［10］HYVARINEN A.Fast and robust fixed－point algorithms for independent component analysis［J］.IEEE Transactions on Neural Network，1999，10(3):626 －634.

［11］YANG H H，AMARI S.Adaptive on － line learning algorithms for blind separation:maximum entropy and minimum mutual information ［J］.Neural Computation，1997，9(5):1457－1482.

［12］劉寧，張偉濤，樓順天.可變步長正交性約束的自然梯度盲信號分離算法［J］.中國鐵道科學，2010，11(6):98－102.

［13］THOMAS P，ALLEN G，AUGUST N.Step － size control in blind sourse separation［C］.Helsinki，Finland:International Workshop on Independent Component Analysis and Blind Sourse Separation，2000:509 －514.

［14］ZHU Xiaolong，ZHANG Xianda.Blind source separation based on optimally selected estimating functions［J］.Journal of Xidian University，2003，30(3):335－339.