雙層圓柱殼內(nèi)外殼振動(dòng)與聲輻射相似性研究

陳美霞，牟彬杰，魏建輝，張曉宇

（華中科技大學(xué) 船舶與海洋工程學(xué)院，武漢 430074）

雙層圓柱殼內(nèi)外殼振動(dòng)與聲輻射相似性研究

陳美霞，牟彬杰，魏建輝，張曉宇

（華中科技大學(xué) 船舶與海洋工程學(xué)院，武漢 430074）

文章基于有限元/邊界元方法計(jì)算了雙層圓柱殼空氣中的固有模態(tài)以及在水下激勵(lì)力作用下的振動(dòng)與聲輻射響應(yīng)，分析了內(nèi)外殼振型的相似性，提出用相似性系數(shù)來(lái)描述振型的相似程度。最后分析了不同軸向位置處的內(nèi)外殼響應(yīng)相似程度，得出了一些結(jié)論：雙層殼內(nèi)外殼具有很強(qiáng)的相似性；實(shí)肋板處的相似性更好。本文為潛艇實(shí)驗(yàn)測(cè)點(diǎn)布置位置的研究提供了一定的理論根據(jù)，具有一定的實(shí)用價(jià)值。

雙層圓柱殼；模態(tài)；振動(dòng)；聲輻射；相似性

牟彬杰（1987-），男，碩士研究生，Email：21381495@qq.com。

1 引 言

雙層圓柱殼是潛艇艙段結(jié)構(gòu)的主要結(jié)構(gòu)形式，研究其在水下激勵(lì)力作用下的振動(dòng)與聲輻射特性具有重大意義。對(duì)于中、低頻范圍內(nèi)的圓柱殼振動(dòng)與聲輻射問(wèn)題，陳美霞、駱東平等[1-4]研究了敷設(shè)阻尼材料以及殼間連接形式對(duì)圓柱殼體的聲輻射性能的影響；商德江、何祚鏞[5]利用有限元軟件Ansys和邊界元軟件Sysnoise對(duì)雙層加肋圓柱殼的水下受激振動(dòng)與聲輻射作了數(shù)值分析研究；張阿漫、姚熊亮[6]等用有限元結(jié)合邊界元的方法研究了結(jié)構(gòu)形式對(duì)圓柱殼振動(dòng)與聲輻射特性的影響。陳美霞、金家坤[7]等用解析法研究了不同連接形式下雙層殼內(nèi)外殼的聲振響應(yīng)。在進(jìn)行潛艇實(shí)驗(yàn)時(shí)，殼體的振動(dòng)和噪聲信號(hào)主要是通過(guò)布置在殼體上的傳感器來(lái)獲得，如何確定傳感器的布置位置和數(shù)量是潛艇實(shí)驗(yàn)中必須解決的關(guān)鍵問(wèn)題之一。賀云南、何琳[8]對(duì)美法海軍提出的傳感器均勻布置方法進(jìn)行了理論分析，結(jié)果表明噪聲測(cè)量系統(tǒng)傳感器均勻布置能夠滿足有限元理論要求。

本文選用了一個(gè)典型的有限長(zhǎng)雙層圓柱殼模型，采用有限元結(jié)合邊界元的方法計(jì)算了水下雙層圓柱殼在激勵(lì)力作用下的振動(dòng)與聲輻射特性，分析了內(nèi)外殼的固有模態(tài)、聲振響應(yīng)的相似性，得出了一些結(jié)論，從而可指導(dǎo)潛艇實(shí)驗(yàn)的傳感器布置，具有一定的工程使用價(jià)值。

2 基本理論

2.1 有限元理論

結(jié)構(gòu)振動(dòng)的有限元方程為：

式中：M、C和K分別為結(jié)構(gòu)的質(zhì)量矩陣，阻尼矩陣和剛度矩陣；u¨、u˙和u分別為結(jié)構(gòu)節(jié)點(diǎn)的加速度向量、速度向量和位移向量；F為作用在節(jié)點(diǎn)上的載荷向量。一旦有限元模型和邊界條件給定，則參數(shù)M、C和K就唯一確定，那么在給定外力F后，就可以求解出結(jié)構(gòu)各節(jié)點(diǎn)上的加速度向量，速度向量和位移向量。

2.2 邊界元理論

對(duì)于單頻聲場(chǎng)，Helmholtz積分方程為[9]：

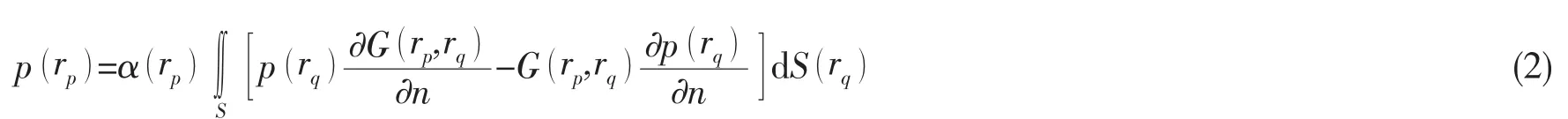
將方程（2）在積分邊界上離散化，將場(chǎng)點(diǎn)定義在邊界上，其位置向量為rp，那么就可以建立起邊界條件與未知主要變量的關(guān)系，則可以得到直接邊界元法的聲學(xué)方程[10]：

式中：A（ω ），B（ω）為影響矩陣。

2.3 模態(tài)振型相似性理論

根據(jù)模態(tài)理論，結(jié)構(gòu)任意頻率下的響應(yīng)可用結(jié)構(gòu)模態(tài)和模態(tài)參與因子線性表示[11]：

其中，q為響應(yīng)值，φi為第i階模態(tài)振型，li為第i階模態(tài)的參與系數(shù)。

在中低頻段，由于兩層殼體之間的耦合作用，兩層殼體的運(yùn)動(dòng)是一致的、整體性的，如果將雙層圓柱殼內(nèi)外殼體的響應(yīng)分別記為q內(nèi)和q外，對(duì)應(yīng)地將各階模態(tài)振型按內(nèi)殼和外殼分開(kāi)表示，則響應(yīng)可以表示為：

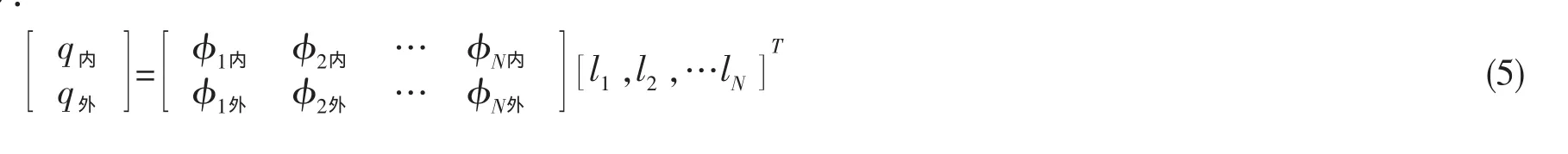
對(duì)于內(nèi)外殼體的響應(yīng)來(lái)說(shuō)，同一模態(tài)的參與因子是一樣的，因此內(nèi)殼和外殼響應(yīng)間的關(guān)系主要由對(duì)響應(yīng)起主要貢獻(xiàn)的模態(tài)對(duì)應(yīng)的內(nèi)殼和外殼間的振型關(guān)系決定。

因此，如果對(duì)內(nèi)外殼響應(yīng)起控制作用的模態(tài)振型很相似，那么內(nèi)外殼的振動(dòng)與聲輻射響應(yīng)也會(huì)很相似。為了量化內(nèi)外殼振型的相似程度，便于更好地說(shuō)明問(wèn)題，本文提出了振型相似性系數(shù)：

式中，φ內(nèi)是內(nèi)殼的振型向量，φ外是外殼的振型向量，φ內(nèi)和φ外都是一個(gè)3n*1的列向量，n是節(jié)點(diǎn)個(gè)數(shù)，φ內(nèi)和φ外做內(nèi)積的時(shí)候?qū)?yīng)的節(jié)點(diǎn)必須是軸向、周向相同位置的節(jié)點(diǎn)，對(duì)應(yīng)節(jié)點(diǎn)的位移向量按照x、y、z的順序進(jìn)行排列。

內(nèi)外殼振型相似性系數(shù)可以直觀地定量判斷內(nèi)外殼振型相似性，β越大，說(shuō)明內(nèi)外殼振型的相似性越好。

為了說(shuō)明相似性系數(shù)的可行性，下面將結(jié)合算例進(jìn)行說(shuō)明。

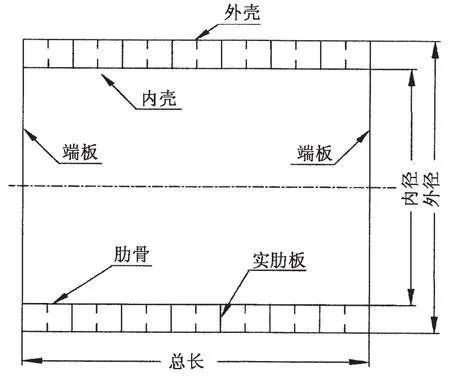
圖1 雙層圓柱殼Fig.1 Double cylinder

3 算例分析

3.1 計(jì)算模型

計(jì)算模型為雙層圓柱殼，如圖1。

幾何參數(shù)為：R1=3.5 m，h1=0.028 m，l1=0.6 m，R2=4.3 m，h2=0.01 m，l2=1.2 m，L=9.6 m。

殼體、環(huán)肋和縱骨材料相同，其彈性模量為2.1e+11 N/m2，泊松比為 0.3，密度為 7 850 kg/m3，損耗因子為0.01。流體的密度為1 000 kg/m3，聲速度為1 500 m/s。

有限元模型如圖2所示（由于對(duì)稱性只取一半模型）

3.2 空氣中模態(tài)分析

首先在Ansys中對(duì)該模型進(jìn)行了空氣中的模態(tài)分析，計(jì)算了前1 000階固有頻率，列出前10階模態(tài)的固有頻率及振型如表1所示。

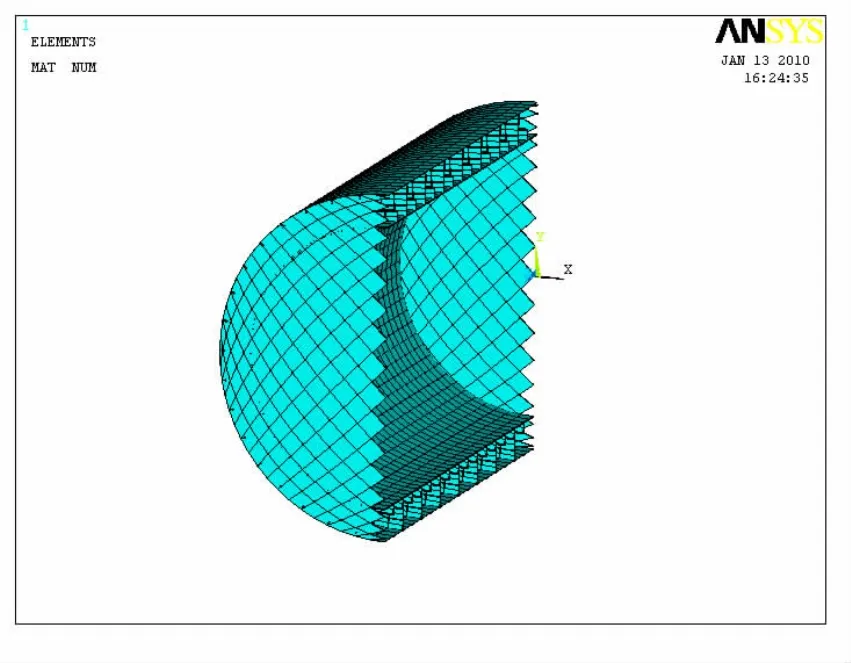
圖2 雙層圓柱殼有限元模型Fig.2 Finite element model of double cylinder

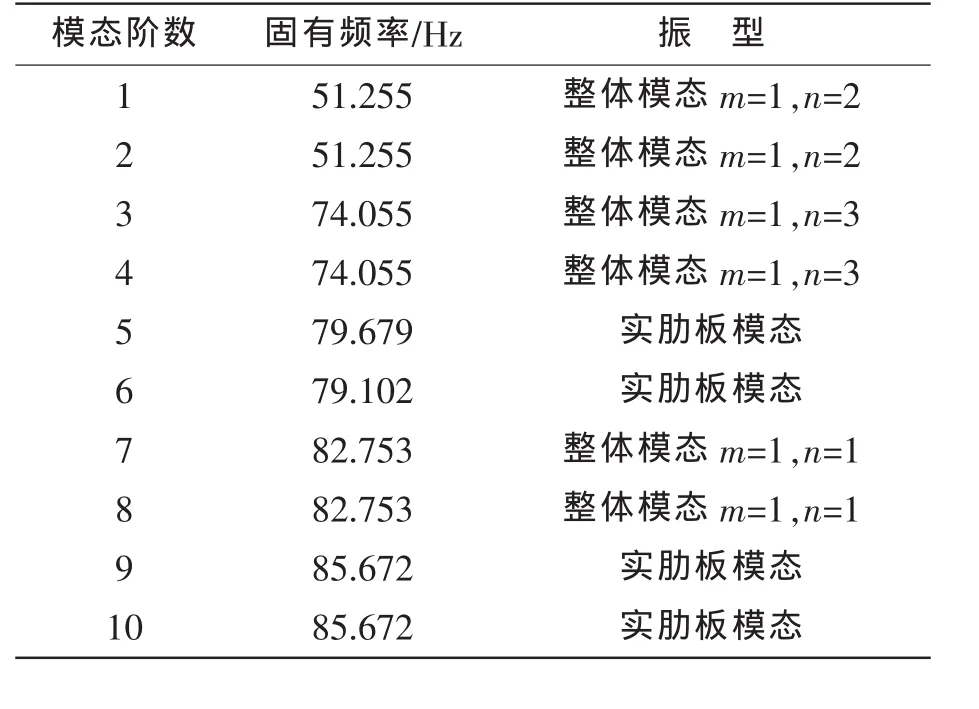
表1 空氣中前10階模態(tài)Tab.1 The first 10 modes in the air

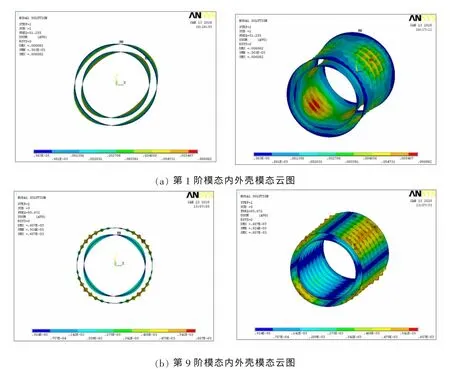
圖3 內(nèi)外殼空氣中模態(tài)云圖Fig.3 Modal fringe of the inner and outer shells in the air

給出其中具有代表性意義的第1和第9階模態(tài)的內(nèi)外殼模態(tài)云圖如圖3所示。

從圖3中可以看到，第1階整體模態(tài)內(nèi)外殼振型具有良好的相似性，而第9階實(shí)肋板局部模態(tài)內(nèi)外殼振型相似性不好。初步判斷，整體模態(tài)的內(nèi)外殼振型相似性要比局部模態(tài)的相似性更好。

3.3 內(nèi)外殼振型相似性

從圖3（a）中可以看到，整體模態(tài)內(nèi)外殼振型十分相似，但是云圖只能定性地反映內(nèi)外殼的相似性，而相似性系數(shù)能定量地反映內(nèi)外殼的相似程度。編程計(jì)算了前100階模態(tài)內(nèi)外殼振型相似性系數(shù)如表2及圖4所示。

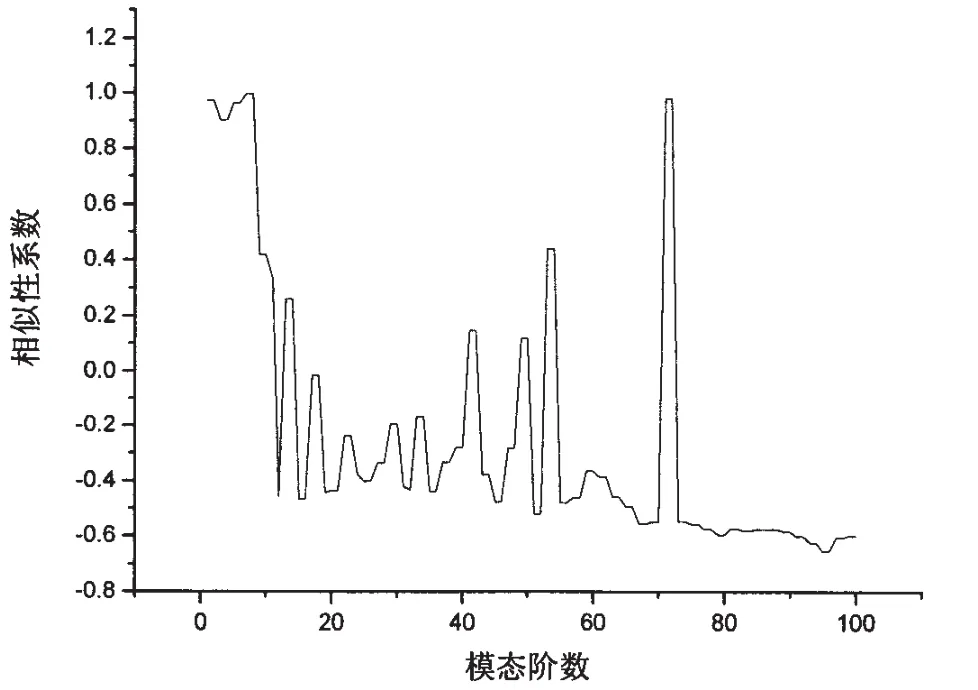
圖4 前100階模態(tài)相似性系數(shù)Fig.4 The similarity coefficients of the first 100 modes

表2 前20階模態(tài)相似性系數(shù)Tab.2 The similarity coefficients of the first 20 modes

從圖4可以看到，前100階模態(tài)除了前幾階整體模態(tài)的相似性系數(shù)很大而外，曲線在第72階模態(tài)處也出現(xiàn)峰值，相似性系數(shù)為β72=0.98。提取第72階模態(tài)的內(nèi)外殼振型云圖如圖5所示。

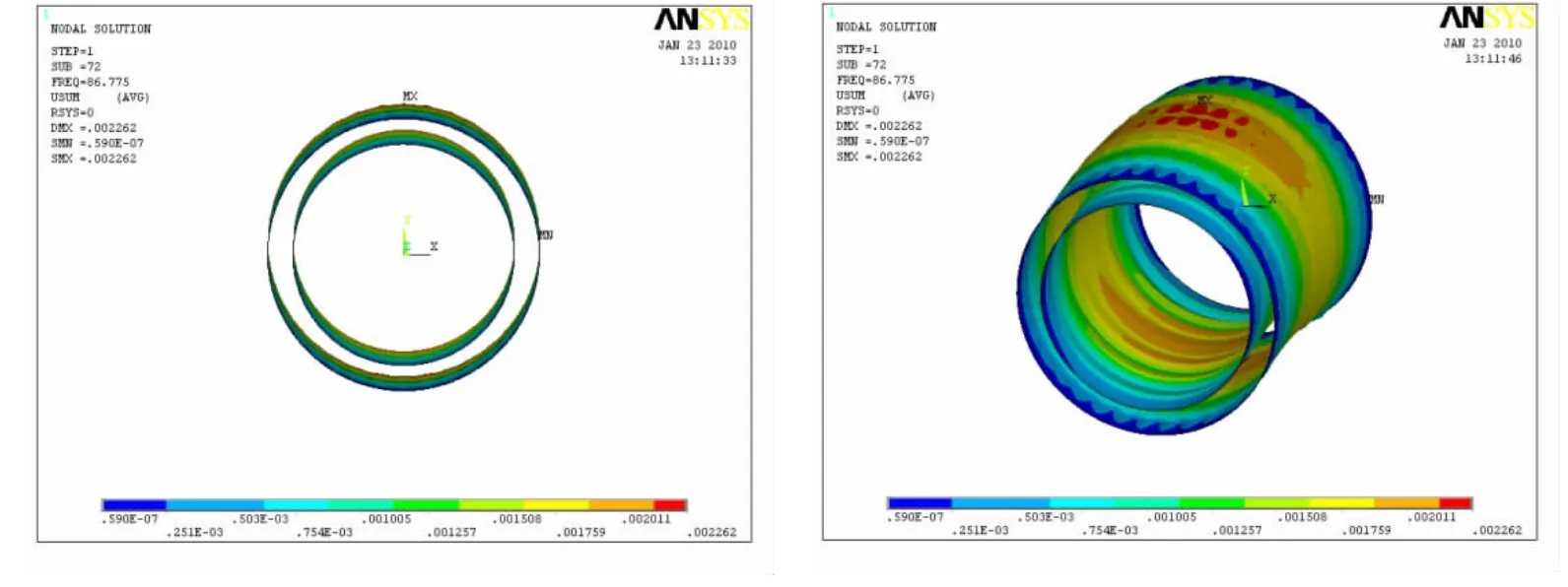
圖5 第72階模態(tài)云圖Fig.5 The 72nd modal fringe

由圖5可以看出，第72階模態(tài)內(nèi)外殼振型呈現(xiàn)整體振動(dòng)的形式，說(shuō)明內(nèi)外殼出現(xiàn)整體振動(dòng)模態(tài)時(shí)，相似程度很高，相似性系數(shù)很大。而其余的模態(tài)相似性系數(shù)都很小甚至為負(fù)值，這是因?yàn)樵谶@些模態(tài)內(nèi)外殼上出現(xiàn)局部振動(dòng)，甚至有內(nèi)外殼振動(dòng)位移方向相反的情況。

由此可知，相似性系數(shù)β可以很好地反映內(nèi)外殼振動(dòng)的相似程度。相似性系數(shù)大的均為內(nèi)外殼的整體模態(tài)，相似性系數(shù)小的均為殼體的局部模態(tài)，相似性系數(shù)為正值說(shuō)明內(nèi)外殼振動(dòng)位移為同相；相似性系數(shù)為負(fù)值說(shuō)明內(nèi)外殼振動(dòng)位移為反相。

3.4 內(nèi)外殼響應(yīng)相似性

計(jì)算模型如3.1所示，在Sysnoise中建立結(jié)構(gòu)有限元與間接邊界元的耦合模型，將3.2計(jì)算得到的1 000階空氣中模態(tài)導(dǎo)入有限元模型中，將邊界元模型的流體屬性定義為水的屬性，在內(nèi)殼L/2處施加徑向點(diǎn)力，計(jì)算得到雙層殼的振動(dòng)響應(yīng)，然后從有限元模型中提取出內(nèi)、外殼體的振動(dòng)響應(yīng)，然后分別以內(nèi)殼體、外殼體作為輻射面建立直接邊界元模型，最后將提取得到的振動(dòng)響應(yīng)作為輻射邊界條件，計(jì)算得到內(nèi)、外殼體水下的均方振速及輻射聲功率如圖6所示。

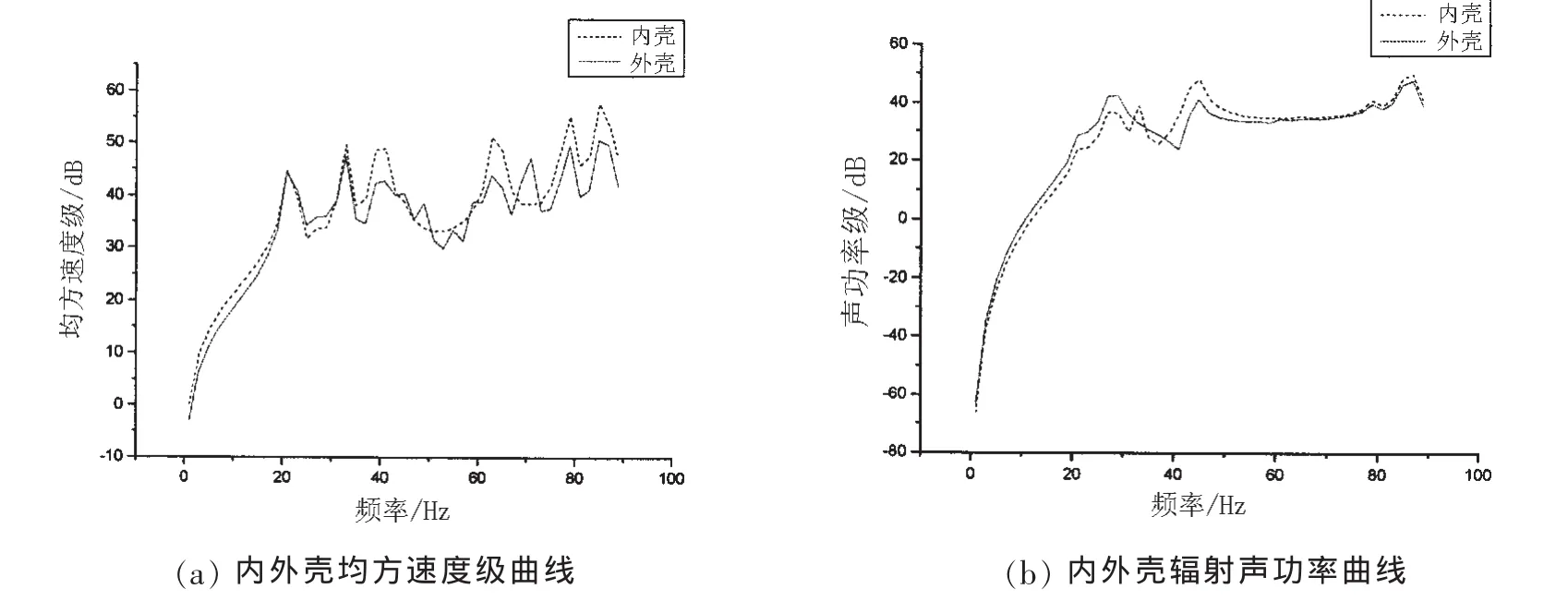
圖6 內(nèi)外殼振動(dòng)聲輻射曲線Fig.6 The curve of vibration and sound radiation of the inner and outer shells

從均方振速曲線上可以看到，整個(gè)頻段，兩條曲線峰值出現(xiàn)的位置基本相同，但外殼振動(dòng)比內(nèi)殼振動(dòng)峰值更多。在40 Hz以下的頻段，內(nèi)外殼振動(dòng)曲線基本一致。內(nèi)殼體振動(dòng)比外殼體略大，這是因?yàn)榧?lì)力作用點(diǎn)在內(nèi)殼。40 Hz以上的頻段，隨著頻率升高，兩均方振速曲線開(kāi)始分離，差距變大。

而從輻射聲功率曲線上可以看到，整個(gè)頻段，兩條曲線峰值出現(xiàn)的位置基本相同，兩條曲線呈現(xiàn)相同的變化規(guī)律。在30 Hz以下的頻段，外殼的輻射聲功率略大30 Hz以上，內(nèi)殼的輻射聲功率略大。

分析一個(gè)典型頻率下內(nèi)外殼振動(dòng)的相似性，由圖 6（a）可知，21 Hz時(shí)，兩條曲線幾乎在同一位置。

在Sysnoise中提取結(jié)構(gòu)振動(dòng)響應(yīng)在21 Hz時(shí)對(duì)應(yīng)的各階模態(tài)參與因子見(jiàn)圖7。由于后面模態(tài)影響很小，只顯示了前800階模態(tài)的模態(tài)參與因子。

從模態(tài)參與因子上可以看出，對(duì)21 Hz結(jié)構(gòu)響應(yīng)起主要控制作用的前5階模態(tài)及對(duì)應(yīng)的模態(tài)參與因子為：第 1 階（5.2E-7），第 692 階（8E-8），第 3 階（3.1E-8），第 5 階（2.3E-8），第7 階（2.1E-8）。

提取這5階模態(tài)振型，內(nèi)外殼都呈現(xiàn)整體振動(dòng)的形態(tài)，計(jì)算得其相似性系數(shù)皆大于0.9。

再分析一個(gè)中高頻率，由圖6（a），兩條曲線在89 Hz處差5個(gè)dB，提取結(jié)構(gòu)振動(dòng)響應(yīng)在89 Hz時(shí)對(duì)應(yīng)的各階模態(tài)參與因子如圖8。

從模態(tài)參與因子上可以看出，對(duì)89 Hz結(jié)構(gòu)響應(yīng)起主要控制作用的前5階模態(tài)及對(duì)應(yīng)的模態(tài)參與因子為：第 592 階（9.4E-8），第 561 階（7.2E-8）， 第 635 階 （5.4E-8）， 第 65 階（5.1E-8），第 48 階（3.8E-8）。

提取這5階模態(tài)振型，內(nèi)外殼振型都呈現(xiàn)局部振動(dòng)的形態(tài)，相似性系數(shù)都小于0.4。

說(shuō)明低頻段的振動(dòng)響應(yīng)主要由前幾階內(nèi)外殼相似性系數(shù)較高的整體模態(tài)來(lái)控制，所以低頻段內(nèi)外殼的響應(yīng)曲線很相似，而隨著頻率升高，參與主要控制的局部模態(tài)增多，因此兩條曲線就逐漸分離。

這表明，在低頻段用內(nèi)殼振動(dòng)來(lái)代替外殼振動(dòng)預(yù)報(bào)聲輻射是可行的。

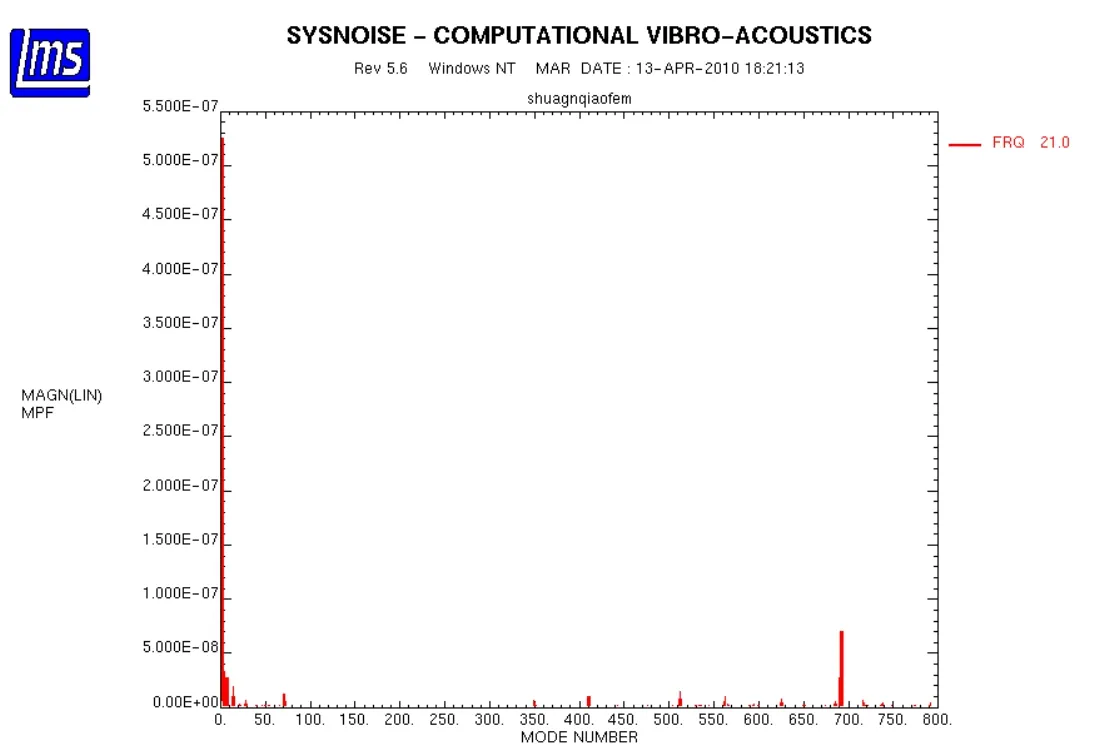
圖7 21 Hz時(shí)各階模態(tài)參與因子Fig.7 Modal participation factor at 21 Hz

圖8 89 Hz時(shí)各階模態(tài)參與因子Fig.8 Participation factor of every mode at 89 Hz

4 實(shí)驗(yàn)測(cè)點(diǎn)布置的研究

前面已經(jīng)說(shuō)明了在進(jìn)行潛艇噪聲測(cè)量的實(shí)驗(yàn)時(shí)測(cè)點(diǎn)布置在內(nèi)殼是可行的，并且提出了內(nèi)外殼振型相似性系數(shù)β。本章在此基礎(chǔ)上，研究測(cè)點(diǎn)布置在肋位，肋中等時(shí)的內(nèi)外殼振動(dòng)響應(yīng)的相似性。

計(jì)算模型、工況及邊界條件與第3章相同，分別提取出內(nèi)外殼對(duì)應(yīng)位置處節(jié)點(diǎn)的振動(dòng)響應(yīng)，編寫(xiě)程序計(jì)算內(nèi)外殼不同軸向位置處振動(dòng)響應(yīng)的相似性系數(shù)α：

式中：ψ內(nèi)是內(nèi)殼振動(dòng)點(diǎn)的振動(dòng)位移向量，ψ外是外殼振動(dòng)點(diǎn)的振動(dòng)位移向量，ψ內(nèi)和ψ外都是一個(gè)3n*1的列向量，n是節(jié)點(diǎn)個(gè)數(shù)，ψ內(nèi)和ψ外做內(nèi)積的時(shí)候?qū)?yīng)的節(jié)點(diǎn)必須是內(nèi)外殼軸向、周向相同位置的兩個(gè)節(jié)點(diǎn)，對(duì)應(yīng)節(jié)點(diǎn)的位移向量按照x，y，z的順序進(jìn)行排列。

本章計(jì)算了5圈（一圈表示一整個(gè)圓周上的點(diǎn)）不同軸向位置的節(jié)點(diǎn)振動(dòng)響應(yīng)的相似性系數(shù)，節(jié)點(diǎn)位置如圖9所示，相似性系數(shù)如圖10所示。

圖9中ai為外殼上的一圈節(jié)點(diǎn)，bi為內(nèi)殼上的一圈節(jié)點(diǎn)，aibi為第i組對(duì)應(yīng)節(jié)點(diǎn)，其中i=1，2，3，4，5。第1組和第5組節(jié)點(diǎn)位于肋位處，激勵(lì)力加在內(nèi)殼b1處，第2、3、4組節(jié)點(diǎn)在兩個(gè)肋位之間等間距分布。

由圖10可知，第1組和第5組的相似性系數(shù)比第2、3、4組的相似性系數(shù)大很多。由此可以得出：肋位處內(nèi)外殼的振動(dòng)相似性要比肋中好，肋位處實(shí)肋板的連接作用增強(qiáng)了內(nèi)外殼振動(dòng)的相似性。

所以，在布置測(cè)點(diǎn)的時(shí)候，應(yīng)優(yōu)先考慮布置在肋位處。

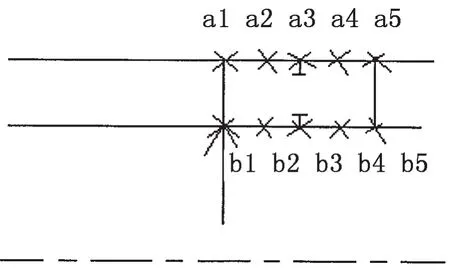
圖9 不同軸向位置的節(jié)點(diǎn)Fig.9 The nodes at various axial positions

圖10 不同軸向位置處內(nèi)外殼振動(dòng)響應(yīng)相似性系數(shù)Fig.10 The similarity coefficients of vibration of the inner and outer shells at various axial positions

5 結(jié) 論

本文通過(guò)對(duì)水下雙層圓柱殼內(nèi)外殼模態(tài)

振型以及振動(dòng)聲輻射響應(yīng)相似性進(jìn)行了分析計(jì)算，提出用相似性系數(shù)來(lái)描述內(nèi)外殼相似的程度，并在此基礎(chǔ)上證明了用內(nèi)殼振動(dòng)響應(yīng)來(lái)預(yù)報(bào)外場(chǎng)輻射聲的可行性，為潛艇實(shí)驗(yàn)測(cè)點(diǎn)布置提供了一定的理論依據(jù)。本文得到的結(jié)論主要有以下幾點(diǎn)：

（1）雙層圓柱殼的內(nèi)外殼整體模態(tài)振型的相似性很好，相似性系數(shù)β在0.9以上，其余的局部模態(tài)的內(nèi)外殼相似性不好，β在0.4以下，β為負(fù)值的模態(tài)表示內(nèi)外殼振動(dòng)方向相反。

（2）內(nèi)外殼體分別的振動(dòng)和聲輻射響應(yīng)曲線在中低頻段很相似，隨著頻率升高，兩條曲線分離，但仍具有相似的變化規(guī)律。這是因?yàn)橹械皖l段的響應(yīng)主要由前幾階整體模態(tài)控制，而這些整體模態(tài)的相似性系數(shù)都在0.9以上，因此內(nèi)外殼的響應(yīng)也很接近。高頻部分的響應(yīng)主要由高階的局部模態(tài)控制，這些局部模態(tài)的相似性系數(shù)都在0.4以下，因此內(nèi)外殼的響應(yīng)曲線分離。

（3）在中低頻段，進(jìn)行潛艇噪聲測(cè)量時(shí)測(cè)點(diǎn)布置在內(nèi)殼是可行的。并且，測(cè)點(diǎn)應(yīng)優(yōu)先考慮布置在實(shí)肋板或托板所在肋位上。

[1]陳美霞,駱東平,楊叔子.殼間連接形式對(duì)雙層殼聲輻射性能的影響[J].振動(dòng)與沖擊,2005,24(5):77-80.

[2]陳美霞,駱東平,彭 旭,等.敷設(shè)阻尼材料的雙層圓柱殼聲輻射性能分析[J].聲學(xué)學(xué)報(bào),2003,28(6):486-493.

[3]陳美霞,駱東平,陳小寧,等.有限長(zhǎng)雙層殼體聲輻射理論及數(shù)值分析[J].中國(guó)造船,2003,44(4):59-67.

[4]陳美霞,駱東平.復(fù)雜雙殼體聲輻射性能分析[J].聲學(xué)學(xué)報(bào),2004,29(3):209-215.

[5]商德江,何祚鏞.加肋雙層圓柱殼振動(dòng)聲輻射數(shù)值計(jì)算分析[J].聲學(xué)學(xué)報(bào),2001,26(3):193-201.

[6]張阿漫,姚熊亮,等.結(jié)構(gòu)形式對(duì)雙層殼聲輻射特性影響研究[J].中國(guó)艦船研究,2007,2(3):3-6.

[7]陳美霞,金家坤,等.內(nèi)、外殼對(duì)水下雙層圓柱殼聲振性能影響分析[J].船舶力學(xué),2009,13(4):628-634.Chen Meixia,Jin Jiakun,et al.Influence by the inner shell and the outer shell on sound-vibration characteristics from double cylindrical shells in water[J].Journal of Ship Mechanics,2009,13(4):628-634.

[8]賀云南,何 琳.潛艇噪聲監(jiān)控系統(tǒng)傳感器優(yōu)化配置研究[C].第十屆船舶水下噪聲學(xué)術(shù)討論會(huì)論文集,中國(guó)造船工程學(xué)會(huì),2005:286-289.

[9]沈杰羅夫（前蘇聯(lián)）著,何祚鏞,趙晉英譯.水聲學(xué)波動(dòng)問(wèn)題[M].北京:國(guó)防工業(yè)出版社,1983.

[10]Sysnoise Rev5.6 User Manual[K].LMS.international.

[11]傅志方,華宏星.模態(tài)分析理論與應(yīng)用[M].上海:上海交通大學(xué)出版社,2000.

Analysis of the vibration and sound radiation similarity between inner and outer shells of double cylindrical shell

CHEN Mei-xia,MOU Bin-jie,WEI Jian-hui,ZHANG Xiao-yu

(College of Naval Architecture and Ocean Engineering,Huazhong University of Science and Technology,Wuhan 430074,China)

FEM/BEM is used to analyze intrinsic modes in air and vibration and sound radiation of the double cylindrical shell in water under force excited state.The similarity coefficient is proposed to describe the similarity between inner and outer shells of double cylindrical shell.Finally,the similarity coefficient between inner and outer shells of double cylindrical shell at various axial positions is analyzed and calculated,and some useful conclusions are drawn:there is a good similarity between inner and outer shells of double cylindrical shell,the similarity at the position of solid floors is better than others.This paper provides some theoretical basis for arranging measuring-point in submarine experiment,which has a certain practical value.

double cylindrical shell;mode;vibration;sound radiation;similarity

TB532

A

1007-7294（2012）11-1329-08

2012-02-01基金資助：國(guó)家自然科學(xué)基金資助項(xiàng)目（50805055）；華中科技大學(xué)自主創(chuàng)新研究基金資助項(xiàng)目（2012QN056）作者簡(jiǎn)介：陳美霞（1975-），女，華中科技大學(xué)船舶與海洋工程學(xué)院副教授，Email：chenmx26@163.com；