過渡過程中萬向鉸傳動偏斜軸系的橫向振動分析

馮昌林，王德石，朱擁勇

（海軍工程大學 兵器工程系，武漢430033）

過渡過程中萬向鉸傳動偏斜軸系的橫向振動分析

馮昌林，王德石，朱擁勇

（海軍工程大學 兵器工程系，武漢430033）

研究了萬向鉸傳動偏斜軸系在過渡過程中的橫向振動問題。將從動軸處理為剛性軸，用一對歐拉角表示從動軸的橫向振動角位移，在建立系統運動坐標系的基礎上，得到萬向鉸的傳遞力矩，將支撐軸承處理為一對正交的彈簧－阻尼器系統，利用改進的歐拉方程推導出過渡過程中萬向鉸傳動偏斜軸系的橫向振動模型。對模型進行數值仿真，分析主動軸角加速度對振動響應的影響。結果表明：萬向鉸傳遞力矩引起系統的自激振動和參數振動，而萬向鉸結構偏斜和誤差偏斜的存在，既能直接影響從動軸所受彎曲力矩的大小，還能引起系統的強迫振動。主動軸角加速度的變化影響系統的穩定性，角加速度越大，經過相同時間后，從動軸振動幅度變得越小。研究工作對進一步確定萬向鉸傳動偏斜軸系的過渡過程運動穩定性具有重要的意義。

萬向鉸；橫向振動；偏斜軸系；過渡過程

1 引 言

偏斜軸系的振動問題是航行體動力學領域中一個重要的研究內容。考慮用萬向鉸（萬向聯軸器）運動約束描述一類軸系的偏斜。由于萬向鉸的運動傳輸特性，即使在主動軸轉速和輸入力矩恒定的定常工況下，從動軸依然表現出波動的轉速，承受波動的傳遞彎矩和軸向轉矩的作用，從而引起軸系的非線性振動。而在過渡過程中，軸系加（減）速的運動沖擊作用將使振動呈現更加復雜的特性。本文旨在研究變工況條件下過渡過程中萬向鉸傳動偏斜軸系的瞬態橫向振動問題。

早在20世紀40年代，《Machine Design》刊物中就基于實驗數據給出了萬向鉸引起的速度、加速度波動表達式[1]，為了避免萬向鉸帶來的軸速波動問題，現行機械設計手冊中也制定了相應的設計與使用規范，并且指出，可以利用等角度平行或相交的雙鉸布置方案消除速度波動，即使這樣，萬向鉸的存在仍然使得軸系的振動問題難以避免。1958年，Rosenberg[2]就曾采取具有集中轉子質量的均勻無質量彈性軸模型對萬向鉸傳動的旋轉軸的橫向振動穩定性進行過研究，得到了偏斜角導致的各種亞臨界失穩條件，研究成果至今仍得到學術界的普遍重視。結果同時表明，振動的穩定性依賴于傳遞力矩的幅度。Iwatsubo和Saigo[3]一起，研究了彈性支撐下的有非跟隨力矩作用的剛性軸，將幾何約束處理為零偏斜角度，即類似于直軸，而考慮萬向鉸約束下的運動波動，給出了力矩表達式，發現了參數失穩和顫振型失穩；并在廣義坐標的選擇方法上，給出了萬向鉸驅動軸橫向振動的Euler坐標描述方法。與此同時，Ota等[4-5]發表的研究報告中，導出了萬向鉸約束中的波動力（力矩），研究了約束激勵下的橫向強迫振動機理與規律，給出了特征參數的實驗研究結果。其后，又進一步考慮了摩擦，將軸系中的從動軸考慮為無質量、偏心且對稱的轉子，將軸柔性處理為集中剛度，研究了參數共振問題，得到了當主軸轉速接近于扭轉、或者橫向固有頻率的偶數倍時，產生參數共振。1997年，Saigo等[7]進一步研究了多剛性軸、多鉸系統，忽略了角速度波動，而注重考察摩擦，研究指出，諸多鉸中一個鉸中的摩擦就能導致不穩定運動；該研究在數學模型上避開了系統的時變特性，故無法處理參數激勵的穩定性問題。盡管由于研究過程中做了較多假設，但還存在進一步的待研究空間，而Rosenberg和Iwatsubo的工作，仍然是研究萬向鉸驅動軸系橫向振動與穩定性的經典成果，對本文的模型研究也具有參考價值。

本文將研究萬向鉸傳動的剛性旋轉軸在過渡過程中的瞬態橫向振動問題。建立偏斜軸系上的一組坐標系，推導萬向鉸傳動的傳遞力矩和從動軸端的軸承力矩，利用剛性體的歐拉旋轉運動方程建立萬向鉸傳動偏斜軸的運動方程，取方程的一次近似進行橫向振動分析，并進行數值仿真。

2 模型描述

取單萬向鉸傳動的偏斜軸系，系統包括主動軸、從動軸和萬向鉸十字軸。主動軸的極向轉動慣量為J1，從動軸的橫向轉動慣量為JL，η為從動軸的極向轉動慣量和橫向轉動慣量的比值，萬向鉸的結構偏斜角為φ，誤差偏斜角為β、γ，從動軸橫向振動的角位移為βL、γL。分別建立主動軸上的固定坐標系X0Y0Z0，十字軸上的固定坐標系XYZ，理想從動軸上的固定坐標系x0y0z0，實際從動軸上的固定坐標系xyz和振動后從動軸上的運動坐標系x2y2z2，如圖1所示。同一點在x2y2z2坐標系和在XYZ坐標系下的坐標變換關系如下：

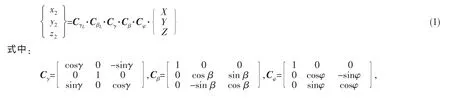
圖1 萬向鉸系統坐標系Fig.1 Reference frames of U-joint system

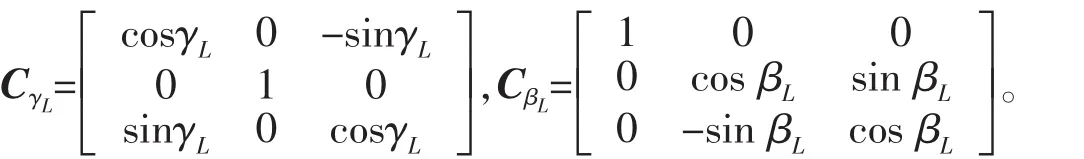
3 力矩分析

本文研究偏斜軸系的橫向振動，因此忽略從動軸的扭轉彈性，從動軸受到的外力主要包括兩部分。第一部分是萬向鉸十字架作用在從動軸上的力，這些力共同產生的合力矩就是主動軸輸入力矩通過萬向鉸傳遞到從動軸上的力矩；第二部分是軸承處的彈簧力和阻尼力，分別對從動軸作用產生彈簧力矩和阻尼力矩。

首先計算萬向鉸傳遞力矩。記主動軸輸入力矩為T0，主動軸角加速度為α，若不考慮十字軸的質量以及十字軸與軸叉之間的摩擦，則主動軸通過軸叉作用于十字軸上的力矩與十字軸通過軸叉作用在從動軸上的力矩相等，而且傳遞到從動軸上的力矩作用在十字軸平面的法線方向。計及振動角βL和γL，應用矢量投影和坐標變換，考慮小角度偏斜及小振動情況，將三角函數展成冪級數形式并忽略高階項后有 cosφ≈cos β≈cosγ≈cos βL≈cosγL≈1，sinφ≈φ，sin β≈β，sinγ≈γ，sin βL≈βL和 sinγL≈γL，忽略高次項后可得萬向鉸傳遞力矩的線性化近似如下：

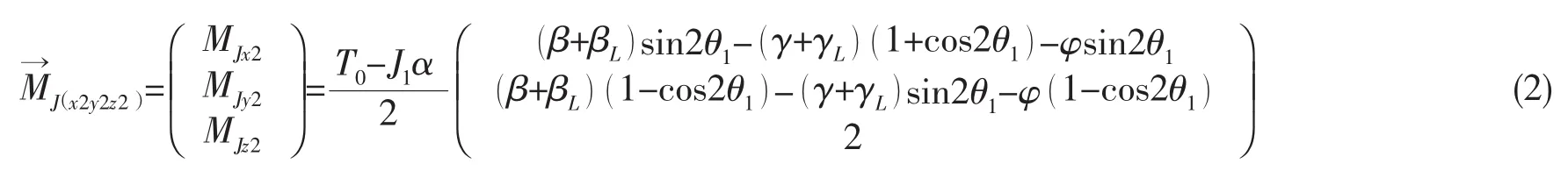
下面計算軸承端的彈簧力矩和阻尼力矩。從動軸一端與萬向鉸相連，另一端由軸承支撐。將軸承處理為互相垂直的兩對彈簧與阻尼器，如圖2所示，其中沿x2軸方向彈簧剛度系數為Kx2、阻尼器阻尼系數為Cx2，沿y2軸方向彈簧剛度系數為Ky2、阻尼器阻尼系數為Cy2。這樣，軸承力矩就轉化為由彈力與阻尼力產生的力矩，而由彈力與阻尼力產生的力矩主要取決于從動軸末端的位移，即從動軸的變形。如圖3所示，未變形時，從動軸向量OA為l→=lk；產生橫向振動后，從動軸形變而引起向量O>?A變化為l→2=lk2；從而，從動軸形變為d→=l→2-l→。

通過運算和簡化可得彈簧力矩和阻尼力矩在運動坐標系x2y2z2中的分量表達式為：

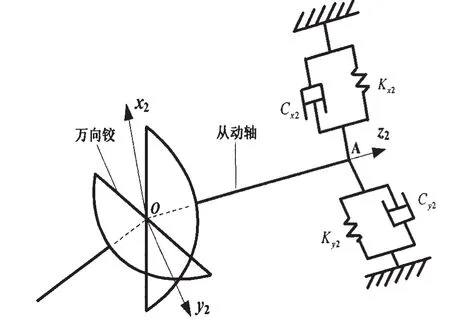
圖2 軸承的彈簧—阻尼器模型Fig.2 The spring-damping model of bearing

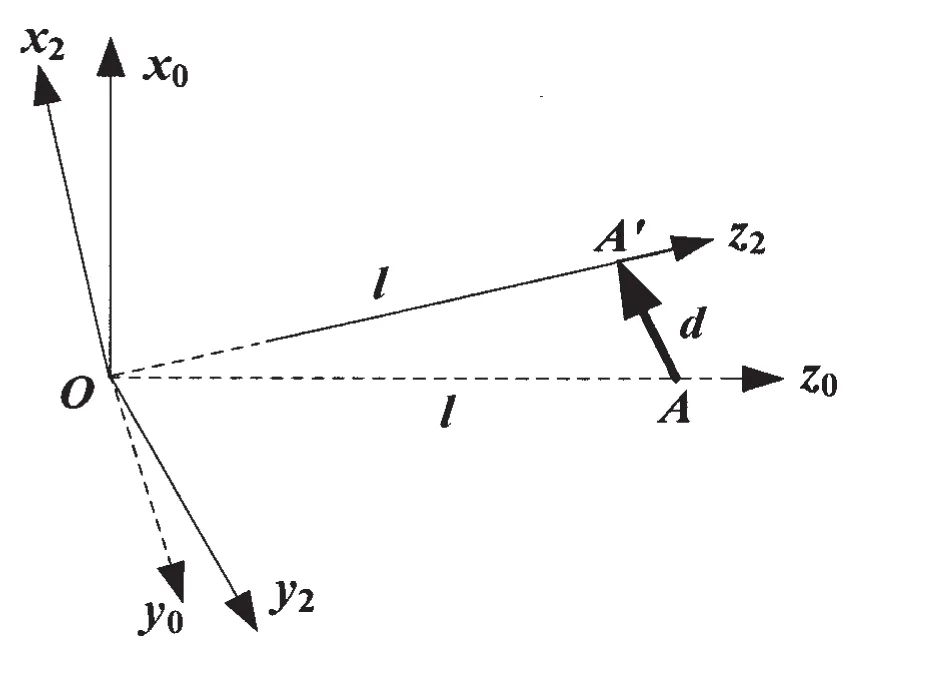
圖3 從動軸的形變Fig.3 The deflection of driven shaft

4 運動方程建立

萬向鉸傳動偏斜軸系的橫向振動可以看成是從動軸繞坐標原點O（萬向鉸十字軸的中心）的轉動。假定Jx2、Jy2和Jz2分別為從動軸繞運動坐標系x2y2z2中Ox2、Oy2和Oz2軸的轉動慣量，利用改進的從動軸繞原點O轉動的普遍運動微分方程（即歐拉方程），就可以建立該萬向鉸傳動的從動軸的運動方程：

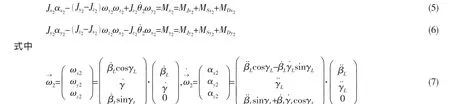
將（2）、（3）、（4）式和（7）式代入（5）式和（6）式可得：

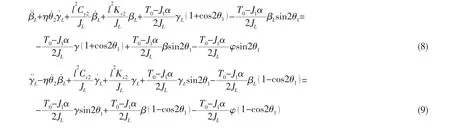
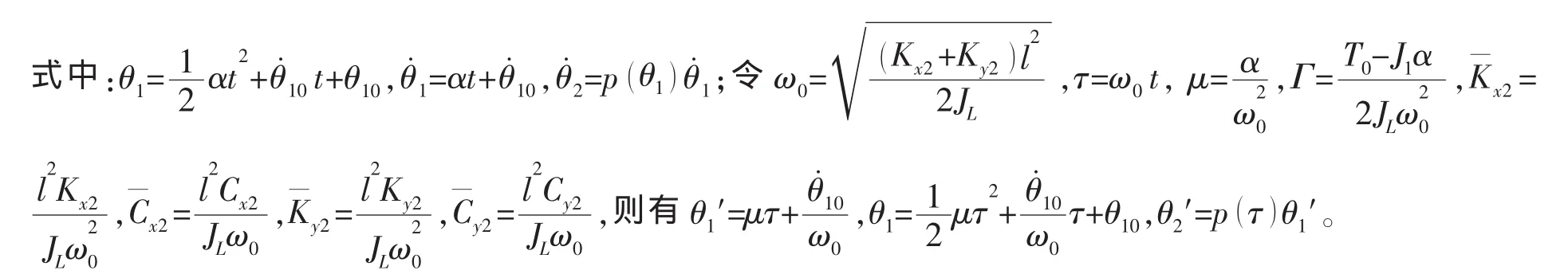
將方程（8）和（9）化為無量綱形式，并寫成矩陣形式如下：

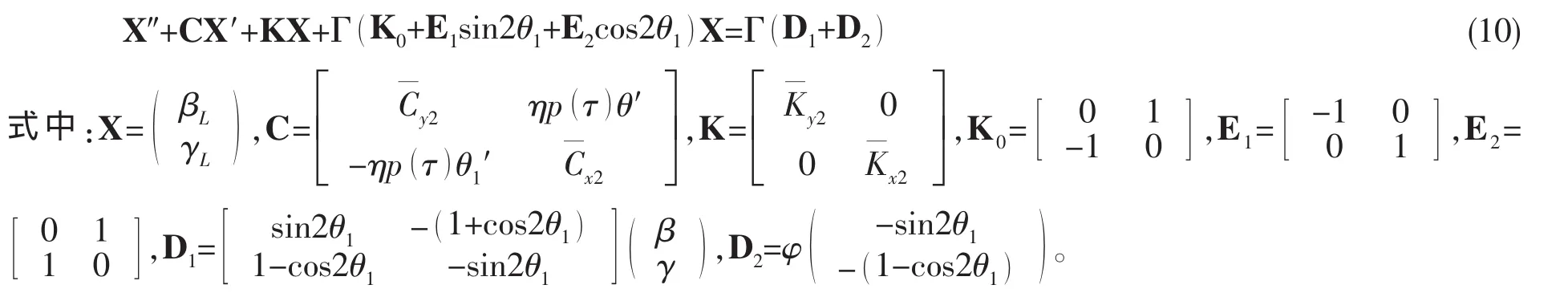
方程（10）左邊第二項的系數矩陣為阻尼矩陣，阻尼矩陣中的元素有的是常數，由系統參數決定，有的是變量，與無量綱時間τ有關；左邊第三項的系數矩陣為剛度矩陣，剛度矩陣是常數矩陣，只與系統參數有關；左邊第四項不含無量綱時間τ的函數，僅與橫向振動本身有關，故它能引起系統的自激振動，產生顫振型失穩；左邊第五項和第六項含有無量綱時間τ的正弦、余弦函數，作為參數激勵，能引起系統的參數共振；方程右邊為強迫振動項，它能引起系統的強迫共振，其中右邊第一項是由萬向鉸結構偏斜引起的，右邊第二項是表示萬向鉸誤差偏斜對萬向鉸驅動的偏斜軸系橫向振動的影響。方程左邊第四、五、六項及右邊項都含有從動軸受到的彎曲力矩，它們均與主動軸輸入力矩T0和主動軸角加速度α有關，是對由萬向鉸傳遞力矩引起從動軸橫向振動的定量描述，可見，對于萬向鉸驅動的偏斜軸系橫向振動問題，萬向鉸傳遞力矩不僅能引起系統的自激振動，還能引起系統的參數振動。

5 模型數值仿真

取一組實驗模型參數：l=0.46 m，從動軸密度ρ=7.83×103kg/m3，從動軸橫截面半經R=2.40×10-3m，n=3.96×10-5，T0=0.3 N·m，Kx2=Ky2=7.740 N/m，Cx2=Cy2=1×10-3N/（m/s），則 JL=πρR2l3/3=4.597×103kg·m2。由文獻[8]可知，當萬向鉸偏斜角較小時，從動軸的角速度波動很小，因此這里忽略從動軸的角速度波動，即p（τ）=1，取偏斜角 φ=5°=0.087 3 rad，β=γ=1°=0.017 5 rad，主動軸角加速度為 α=0.02 rad/s2時，方程（10）對應的系統橫向振動響應 βL和 γL如圖 4 所示，其中，βL和 γL的單位為弧度（rad），時間 t的單位為秒（s），以下所有系統響應圖中的單位均與此相同。由圖4可知，在這組參數條件下系統的橫向振動響應是不穩定的，振動幅度隨時間增加而增大；βL和γL的振動響應數值不同，但是變化規律相同。

圖4 系統響應圖（α=0.02 rad/s2）Fig.4 Response of system(α=0.02 rad/s2)

過渡過程與平穩工況下的明顯不同就是要考慮主動軸的加速轉動，為了研究角加速度對系統響應的影響，令其它參數保持不變，畫出α=0.04 rad/s2和α=0.08 rad/s2時系統的橫向振動響應βL如圖5和圖6所示。比較圖4、圖5和圖6可以看出，α=0.02 rad/s2時，βL由開始時的0.007 rad經過100 s后增加到0.015 rad；α=0.04 rad/s2時，βL經過100 s后幾乎保持在0.007 rad左右，幅度沒有變化；而α=0.08 rad/s2時，βL由開始時的0.007 rad經過100 s后減小到0.003 rad。因此主動軸角加速度的變化影響系統的穩定性，角加速度越大，經過相同時間后，振動幅度變得越小；在本文所取的實驗模型參數條件下，α＜0.04 rad/s2時系統是不穩定的，α≥0.04 rad/s2時系統是穩定的。

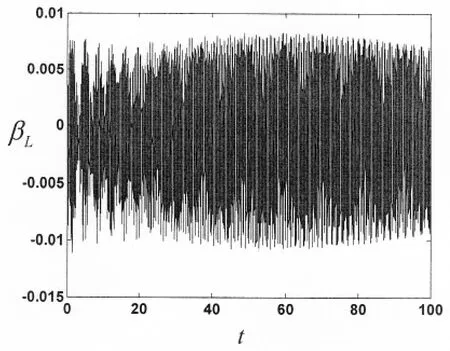
圖5 系統響應圖（α=0.04 rad/s2）Fig.5 Response of system(α=0.04 rad/s2)

圖6 系統響應圖（α=0.08 rad/s2）Fig.6 Response of system(α=0.08 rad/s2)

當然，在萬向鉸及變工況的共同作用下，偏斜旋轉軸系的穩定性是復雜的，系統包含自激振動、參激振動和強迫振動成分，而且會表現出多種共振形式，包括和型組合共振、差型組合共振、主共振及超諧波共振等，對過渡過程中萬向鉸傳動偏斜軸系橫向振動的詳細穩定性分析將在后續文章中進行研究。

6 結 論

本文研究了過渡過程中萬向鉸傳動偏斜軸系的橫向振動問題。首先，將偏斜旋轉軸的橫向振動以從動軸的角位移βL和γL表示，在建立系統運動坐標系的基礎上，將支撐軸承處理為一對正交的彈簧－阻尼器系統，利用歐拉方程推導出了過渡過程中萬向鉸傳動偏斜軸系的橫向振動模型，該模型為兩自由度參數激勵系統。從分析該模型可以看出，萬向鉸傳遞力矩引起了系統的自激振動和參數振動，而萬向鉸結構偏斜和誤差偏斜的存在，既能直接影響從動軸所受彎曲力矩的大小，還能引起系統的強迫振動。利用龍格－庫塔法對該偏斜軸系橫向振動響應進行了數值仿真，仿真結果表明主動軸角加速度的變化影響系統的穩定性。本文得到的振動模型為后續研究分析過渡過程中萬向鉸傳動偏斜軸系的橫向振動穩定性奠定了基礎。

[1]Jermy L E．Velocity and acceleration analysis of universal joints[J]．Machine Design,1942,14(11):93-94．

[2]Rosenberg R M,Ohio T．On the dynamical behavior of rotating shafts driven by universal(Hooke)couplings[J]．ASME Journal of Applied Mechanics,1958,25(1):47-51．

[3]Iwatsubo T,Saigo M．Transverse vibration of a rotor system driven by a cardan joint[J]．Journal of Sound and Vibration,1984,95(1):9-18．

[4]Ota H,Kato M．Lateral vibration of a rotating shaft driven by a universal joint-1st report,generation of even multiple vibrations by secondary moment[J]．Bulletin of JSME,1984,27(231):2002-2007．

[5]Ota H,Sugita H,Kato M．Lateral vibration of a rotating shaft driven by a universal joint-2nd report[J]．Bulletin of JSME,1985,28(242):1749-1755．

[6]Kato M,Ota H．Lateral excitation of a rotating shaft driven by a universal joint with friction[J]．Journal of Vibration and A-coustics,1990,112:298-303．

[7]Saigo M,Okada Y,Ono K．Self-excited vibration caused by internal friction in universal joints and its stability method[J]．Journal of Vibration and Acoustics,1997,119:221-229．

[8]馮昌林,王德石,朱擁勇．變工況條件下萬向鉸驅動軸的運動特性分析[C]．龔自正．數學力學物理學高新技術交叉研究進展—2010卷．北京:科學出版社,2010:479-484．

Lateral vibration analysis of misaligned shafting driven by a universal joint during transient process

FENG Chang-lin,WANG De-shi,ZHU Yong-yong

(Department of Weaponry Engineering,Naval University of Engineering,Wuhan 430033,China)

The lateral vibration of misaligned shafting driven by a universal joint during transient process is investigated.The driven shaft is assumed to be a rigid shaft,and the angular deflection of lateral vibration is described by a pair of Euler’s angles,the components of the moment transmitted by the universal joint with respect to a moving frame are obtained.The bearing is modeled by pairs of springs and dampers,then the lateral vibration differential equations were established applying the modified version of Euler’s equations.Using direct numerical integration for a set of parameter values,the response of lateral vibration is found,and the effects of angular acceleration on vibration response are analyzed.The results indicate that the transmitted torque causes not only parametric vibrations but also self-excited ones,the misalignments of universal joint affect the bending moment acting on the driven shaft directly,and cause the forced resonances of system.The angular acceleration of the driving shaft affects the stability of system,the vibration amplitudes decrease with the increase of angular acceleration.The research work makes sense in confirming the dynamic stability of misaligned shafting driven by universal joint during transient process.

universal joint;lateral vibration;misaligned shafting;transient process

TH133.4

A

1007-7294（2012）11-1314-07

2011-11-17

國家自然科學基金資助項目（50875259）和教育部留學回國人員科研啟動基金資助項目

馮昌林（1983-），男，海軍工程大學博士生，E-mail:fcl_325@126.com；

王德石（1963-），男，海軍工程大學教授，博士生導師。