邊坡破裂過程的斷裂力學分析
薛付霞,王成
(重慶交通大學土木工程學院,重慶400074)
0 引言
目前,基于斷裂力學的邊坡穩定性分析已經引起重視,比如裂紋線場分析方法[1-2]、巖體節理內壓致裂解析研究[3]、強度準則的探討[4]、邊坡穩定分析[5]等,但是目前還沒有基于斷裂力學的邊坡穩定性判斷方法。本文用斷裂力學和有限元方法[6]相結合對邊坡進行分析,得到邊坡破裂時更加趨近于I型破壞,以及當裂縫長度超過臨界長度時邊坡會失穩的結論。
1 斷裂力學理論基礎
邊坡的破壞模式屬于Ⅰ-Ⅱ復合型,位移法求解應力強度因子的表達式如下[7]:
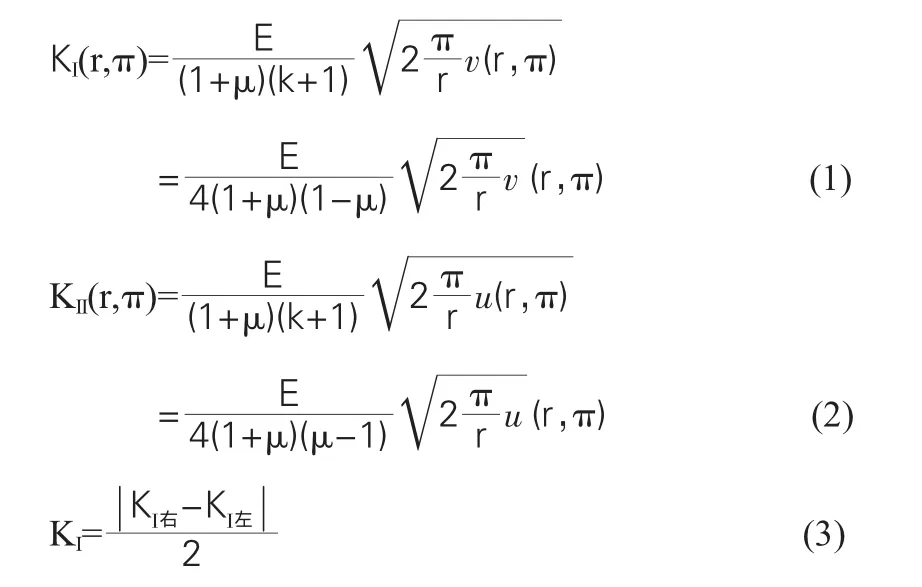

其中,E為材料的彈性模量,ν為材料的泊松比,v(r,π)和u(r,π)分別為裂縫兩側距離裂縫尖端距離為r的點沿裂縫張開方向和裂縫滑開方向的相對位移,位移可通過ansys計算;Ki左為裂縫左側點的應力強度因子,Ki右為裂縫右側點的應力強度因子,如圖1所示。裂紋尖端應力強度因子通過計算其附近點的應力強度因子得到[7]。
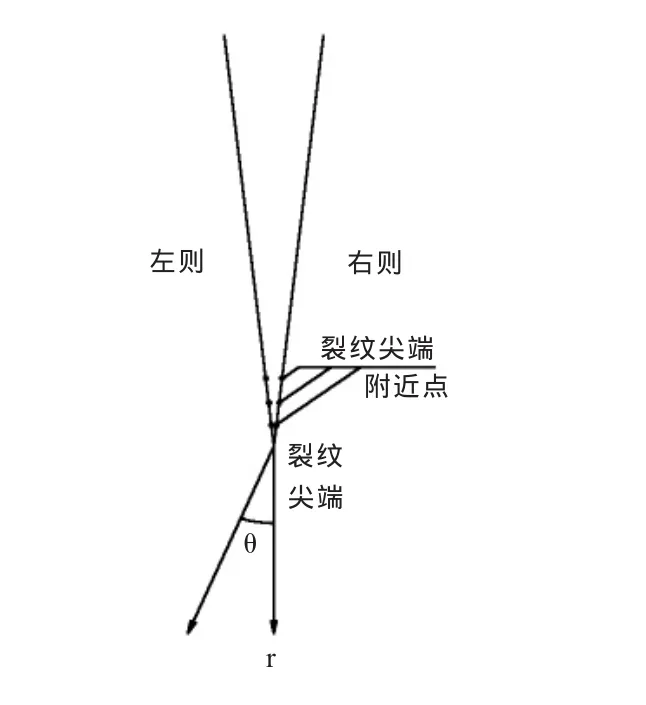
圖1 裂紋尖端左右側示意圖
求解裂紋擴展角的公式為[7]:
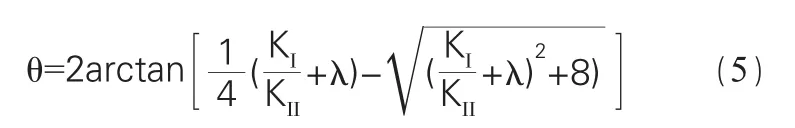
Ⅰ-Ⅱ復合型裂縫的斷裂判據及破壞準則為[4]:

其中,KIC為材料的Ⅰ型斷裂韌度,KE為Ⅰ-Ⅱ復合型裂縫的等效應力強度因子。
2 算例分析
主要通過算例,用ansys分析裂縫的擴展過程。邊坡參數為:坡高12m,坡 頂 寬6m,坡 底 寬12m,坡腳正切值為2,如圖2。邊坡材料參數見表1。[5]
有人可能會問,一歲半小孩能聽懂這些話嗎?我從來不把他當小孩,他平時做這些的時候我經常用語言給他描述他的行為,所以我寫下來的這些內容他是可以聽得懂的。
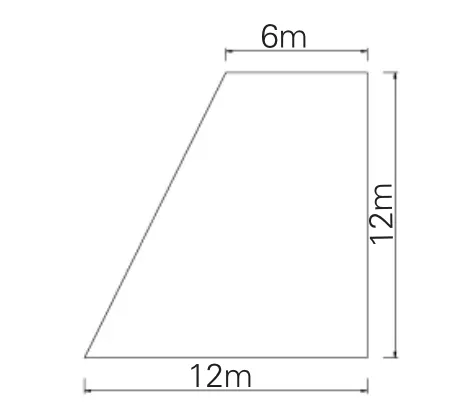
圖2 邊坡坡形
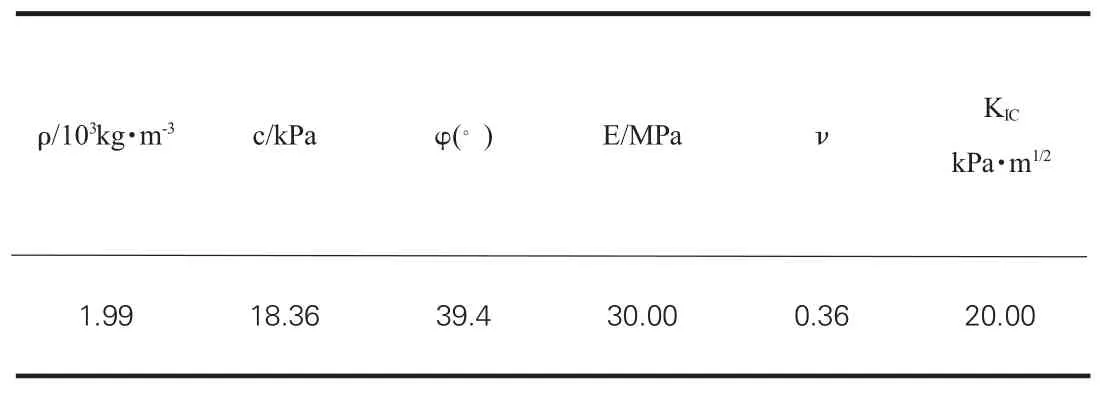
表1 邊坡土的參數
2.1 確定邊坡最易開裂位置
用ansys求在重力作用下的應力分布情況(圖3),可以得到坡頂應力最大的位置,第一條裂縫出現在應力最大點附近。由應力等值線圖可以看出坡頂最易開裂位置在距離坡緣3.7m左右處。

圖3 應力等值線圖
通過在應力最大的點附近設置相同長度的裂縫并求解其應力強度因子的大小,應力強度因子最大處即為比較精確的邊坡最易開裂位置。
在距離坡緣3.7m處設置一條0.5m的裂縫,為了求其尖端應力強度因子,在尖端附近兩側共取6個點,并讀取此時的位移情況,將位移值代入公式(1)、(2),求得的裂紋尖端這六個點所對應的應力強度因子如表2所示。
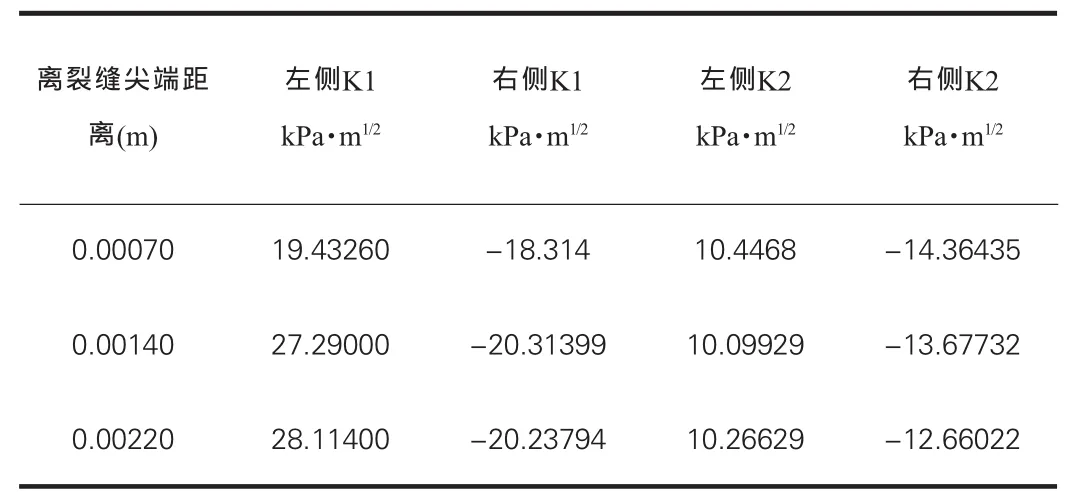
表2 裂紋尖端兩側選取的節點所求的應力強度因子
將這六個應力強度因子進行線性擬合,得到裂紋尖端處的應力強度因子:KⅠ左=16kPa·m1/2, 同理:KⅠ右=-17.4kPa·m1/2,KⅡ左=6.4kPa·m1/2,KⅡ右=-15kPa·m1/2, 將以上數據代入公式(3)、(4)得到此裂紋尖端的應力強度因子為:KⅠ=11.9kPa·m1/2,KⅡ=10.7kPa·m1/2,KE2=11.9^2+10.7^2=256.1, 此時,KE2/KIC2=0.64<1,所以在距坡緣3.7m處此裂縫不會開裂。
在距坡頂邊緣3.7m附近分別按照同樣方法計算,應力強度因子結果如圖4。
圖3可以看出,在裂紋長度為0.5m時,裂紋均穩定,不會擴展,但是,在3.5m處雖然裂縫未發展,但此位置KE最大,因此,最易開裂位置確定為距離坡頂邊緣3.5m處。
2.2 求解臨界縫長
此邊坡在只受重力作用下用傳統的極限平衡法來分析時,是穩定的。本文認為,邊坡破壞受內部裂縫的影響,邊坡所受的外力越大,邊坡的臨界縫長越小即邊坡越容易破壞。本算例所受外力較小,臨界縫長就會越大,即實際情況中裂縫不容易達到這個長度,但是臨界縫長依然存在。
在3.5m處設置不同長度的裂縫試算,確定臨界縫長。當裂縫長度取0.7m時,KE2/KIC2=0.95,裂縫不會擴展;當縫長取0.8m時,KE2/KIC2=1.015>1,此時裂縫會擴展,所以臨界縫長取0.8m。
2.3 裂縫的擴展
在距坡頂邊緣3.5m處設置0.8m長的裂縫,得KⅠ=28.85kPa·m1/2,KⅡ=14.9kPa·m1/2,KE2=28.85^2+14.9^2=379.5,此時KE2/KIC2=2.636>1,所以此裂縫會繼續擴展。將KⅠ、KⅡ代入公式(5)得到開裂角θ=40.9○。即此裂縫將以40.9○往下擴展,出現第二條裂縫。為了簡化計算,本文假設每條裂縫的擴展長度都是0.8m,同時為了所求的破壞面的準確性,每條裂縫的擴展角都是通過計算得到的(同第一條裂縫)。
同理,直到第十三條裂縫出現,邊坡內部裂縫貫通,所得到的破壞面即為基于斷裂力學求得的邊坡破壞面,如圖5。由于計算過程的簡化,所得到的破裂面沒有經過坡腳,但是距離坡腳不遠。裂縫擴展過程中相關數值的變化如表3。
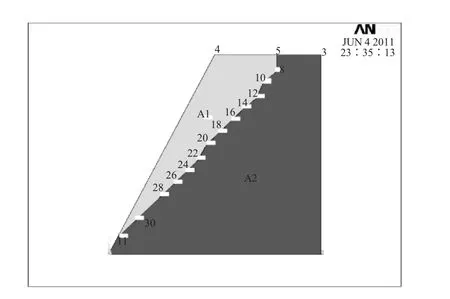
圖5 斷裂力學求得的邊坡破壞面
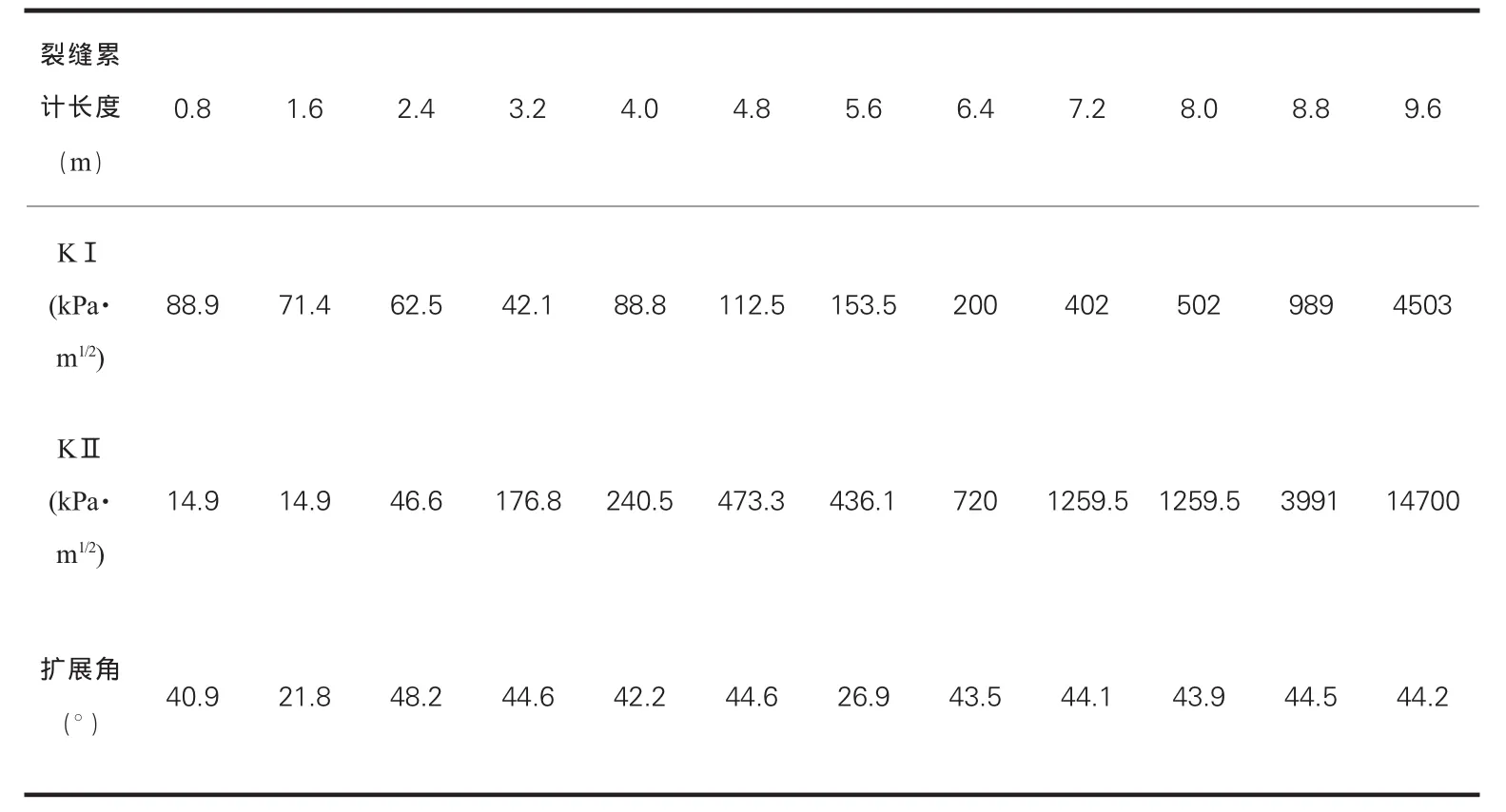
表3 裂縫擴展過程中相關數值變化
圖6為裂縫擴展過程中KⅠ/KⅡ變化圖,從圖中可以看出,第一條裂縫的KⅠ是KⅡ的6倍,所以邊坡破壞更傾向于Ⅰ型破壞。由于本文忽略了已經開裂的滑動體與穩定體之間的摩擦力,所以在裂紋擴展了約1/4后出現了非常趨近于Ⅱ型破壞的現象。
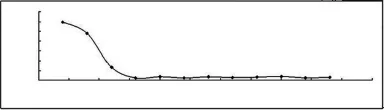
圖6 裂縫擴展過程中KⅠ/KⅡ變化圖
3 結論
邊坡內部天然存在很多細微裂紋,本文認為邊坡破壞是裂紋貫通的過程。斷裂力學分析邊坡的思想對巖質和土質邊坡都適用,但是本文只對粘土邊坡進行了分析。
運用線彈性斷裂力學原理結合有限元軟件分析粘土邊坡破壞過程,得出以下適用于粘土邊坡的結論:
(1)當坡頂裂縫長度大于臨界縫長時,應力強度因子超過斷裂韌度,邊坡失穩。
(2)邊坡的破壞雖然屬于Ⅰ-Ⅱ復合型,但其破壞更加趨近于Ⅰ型。
(3)本文方法確定的邊坡破壞面與實際的破壞面接近,表明該方法的可行性和正確性。
[1]王成.裂紋線場分析方法在巖石力學中的應用[J].巖石力學與工程學報,2010,29(1),3254-3258.
[2]朗惠芳,代彤.基于裂紋線場分析法的滑坡失穩機理分析[J].山西建 筑 ,2009,55 (17),105-106.
[3]王成,鄧安福.巖體節理內壓致裂解析研究[J].巖石力學與工程學報,2002,21(3),123-126.
[4]王桂堯,孫宗顧,徐紀成.巖石壓剪斷裂機理及強度準則的探討[J].巖土工程學報,1996,18(4),68-74.
[5]張廼龍,郭小明,王向東.黏土坡穩定性的斷裂力學分析[J].東南大學學報,自然科學版,2010,40(5),1029-1033.
[5]陳芳,王生楠.I-Ⅱ復合型裂紋的應力強度因子有限元計算分析[J].機械設計與制造2009(8),20-21.
[7]程勒,趙樹山.斷裂力學[M].北京:科學出版社,2006.

