通過PVDF陣列測量體積位移的實驗研究*

毛崎波

(南昌航空大學飛行器工程學院，南昌330063)

近幾年來，壓電智能材料(Piezoelectric Smart Material)特別是具有密度低、機械韌性好、可塑性強等優點的高分子壓電薄膜PVDF(Polyvinylidene Fluoride)作為壓電式傳感器在結構聲有源控制ASAC(Active Structural Acoustic Control)中的應用越來越引起關注[1－6]。由于振動結構的聲功率為其表面法向速度的函數，表面法向速度的分布不同對聲功率的貢獻不同，所以合理的壓電式傳感器應該只測量對聲輻射起主要貢獻的結構振動。最近有學者提出通過抵消體積位移(Volume Displacement)設計ASAC系統，并對壓電式體積位移傳感器的設計方法進行了理論和實驗研究[7－9]。這一方法的主要特點是利用模態的正交性得到特定形狀的PVDF傳感器形狀，本文稱之為“模態方法”。但是隨著研究的深入，發現這種傳感器設計方法存在如下問題難以解決:對于一種邊界條件，就需要一種特定形狀的PVDF傳感器，邊界條件的變化有可能使所設計的PVDF傳感器的輸出有很大的誤差。PVDF薄膜的形狀有可能很復雜，難以加工。

[10－13]提出了另一種模態傳感器的設計方法，其基本思路為通過在振動結構表面上布置一組相同形狀的矩形PVDF薄膜陣列，然后通過設計這組PVDF陣列的加權系數，測量振動結構的體積位移或聲輻射模態。在此前發表的論文中，作者對此進行了大量的理論和實驗研究[9－11，14－16]。進一步的研究表明通過這種方法所設計的PVDF薄膜并不需要覆蓋整個結構的表面。但是這種方法的基本思想還是利用模態的正交性，所以在確定PVDF傳感器的加權系數時必須預先解得結構的結構模態(振型函數)。

為了解決這些問題，本文以一未知邊界條件的振動梁為例，提出通過測量 PVDF陣列中各個PVDF薄膜與激勵力之間的頻率響應函數，并結合偽逆方法和Tikhonov正則化方法設計PVDF陣列的加權系數，從而得到所需的體積位移。

1 基本理論

假設有一鑲嵌在無限障板中的振動梁，長度為Lx，寬度為 Ly，厚度為 h。根據參考文獻[7，10]可知，體積位移D為振動梁表面法向位移w(x)在整個梁表面上的積分，即

從聲輻射模態理論可知，體積位移與第1階聲輻射模態的幅值成正比，在低頻時第1階聲輻射模態對聲功率起主要貢獻[3－4]。Berry[17]進一步指出，當作用在梁上激勵力的無量綱頻率k·Lx?1時(其中k為波數，k=ω/c0，ω為激勵力頻率，c0為聲速)，聲功率W可表示為

式中ρ0為空氣的密度。

從式(2)可知，低頻時梁的聲功率與體積位移有直接關系。如果抵消了體積位移，就能使振動結構低頻時的聲功率明顯降低。

2 PVDF傳感器的設計

考慮在振動梁上均勻布置N塊同樣形狀的矩形PVDF薄膜，如圖1所示。假設第n個PVDF的其輸出電荷為Qn，為了測量各階模態坐標，我們通過對每個PVDF設計不同的加權系數，其基本思路如圖2所示。從圖2中可以看出，經過加權后，這組PVDF傳感器的輸出為

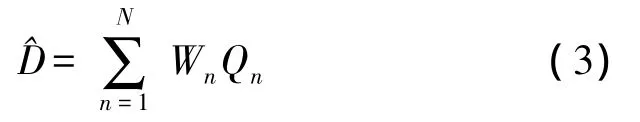
式中:Wn表示第n個PVDF傳感器未知的加權系數。

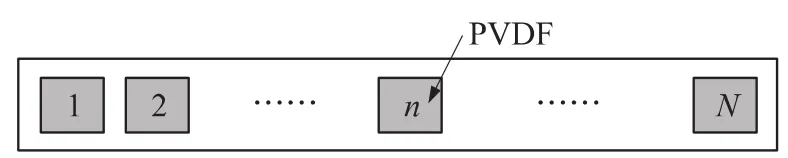
圖1 PVDF示意圖

圖2 通過PVDF陣列測量體積位移示意圖

下面的任務是如何設計恰當的加權系數W使得經過加權后這組PVDF陣列的輸出電荷 ^D等于體積位移D。

考慮到在實際工程應用中，一般情況下振動梁的邊界條件或模態信息為未知。所以我們無法通過傳統的模態方法[10－13，18]設計 PVDF 陣列的加權系數。為此我們提出偽逆方法設計PVDF陣列的加權系數，首先假設在一定頻率范圍內，通過一已知激勵力下的體積位移D(ω)，并測量到該激勵力與PVDF薄膜之間的頻率響應函數Gn(ω)。

由式(3)可知，通過PVDF測量的體積位移D=^D可以表示為頻率響應函數Gn(ω)和相應PVDF加權系數Wn的線性組合，即

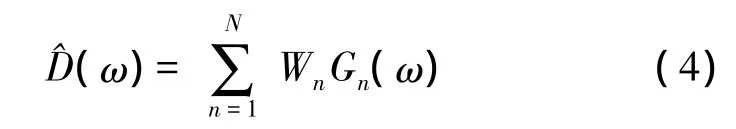
假設在式(4)中選取L(L＞N)個頻率，則式(4)可以進一步表示為矩陣形式，即

式中:G矩陣的(l，n)元素為第n個PVDF在頻率為ωl時的輸出電荷。G和為復數矩陣，而W為實向量。

把式(5)代入式(6)得

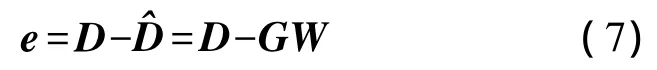
從式(7)可知，可以定義誤差準則J為

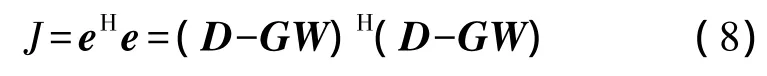
可以通過最小化式(8)即可得到PVDF陣列的加權系數向量W。注意到式(8)中WHGHGW=DHD=|D|2＞0，所以矩陣GHG為正定。式(8)為標準Hermitian二次方形式，具有唯一的最小值。根據線性均分優化理論，可以得到最優解:

式中:G+=[GHG]－1GH為G矩陣的偽逆。上標 H表示復共軛轉置。

通過式(9)直接求解加權系數向量W存在的主要困難在于無法保證矩陣G不是病態的，有可能導致G矩陣中的測量誤差在計算過程中被非線性放大，使得通過式(9)得到的加權系數偏離精確解。所以本文引入Tikhonov正則化方法求解方程(8)，Tikhonov正則化的基本思路是在式(8)的誤差準則中加入一額外的約束，式(8)中的誤差準則重新表示為[19－21]

式中:α為正則化參數(正實數)。在未知測量誤差的情況下，可以通過廣義交叉驗證[18]GCV(Generalized Cross-Validation)方法確定正則化參數α，即

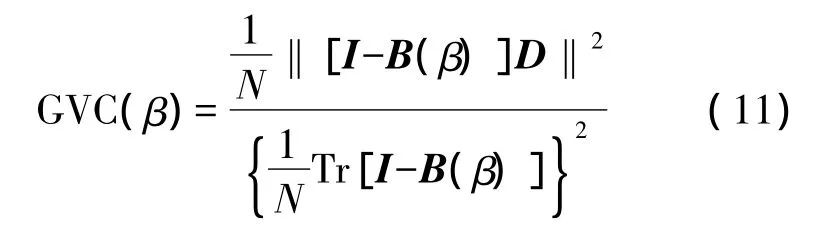
式中:Tr表示括號內矩陣的對角元素之和，B(β)=GT(GGT+αI)－1。

由參考文獻[19－21]可知，式(10)的最優解為

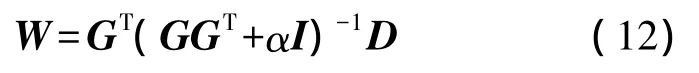
這樣通過式(12)就可得到測量體積位移的PVDF陣列加權系數W。需要指出的是，本文方法不需要結構的模態信息或邊界條件。還需要指出的是，只要把PVDF的電流信號作為輸出，就可以測量體積速度[9]。

3 實驗研究

為了驗證本文的設計方法，取一鋁梁長Lx=500 mm，寬Ly=40 mm，厚h=3.3 mm進行實驗研究。通過在梁上均勻粘貼N=10塊相同形狀的矩形PVDF薄膜作為傳感器測量該粱的體積位移，實驗裝置如圖3所示。實驗測量的前7階固有頻率如表1所示，在表1中同時列出了該梁在兩端簡支和兩端固定的前7階固有頻率的理論值。從圖2和表1可以發現，實驗裝置中振動梁的邊界條件介于簡支和固定之間。PVDF傳感器的物理參數如表2所示。

圖3 實驗照片

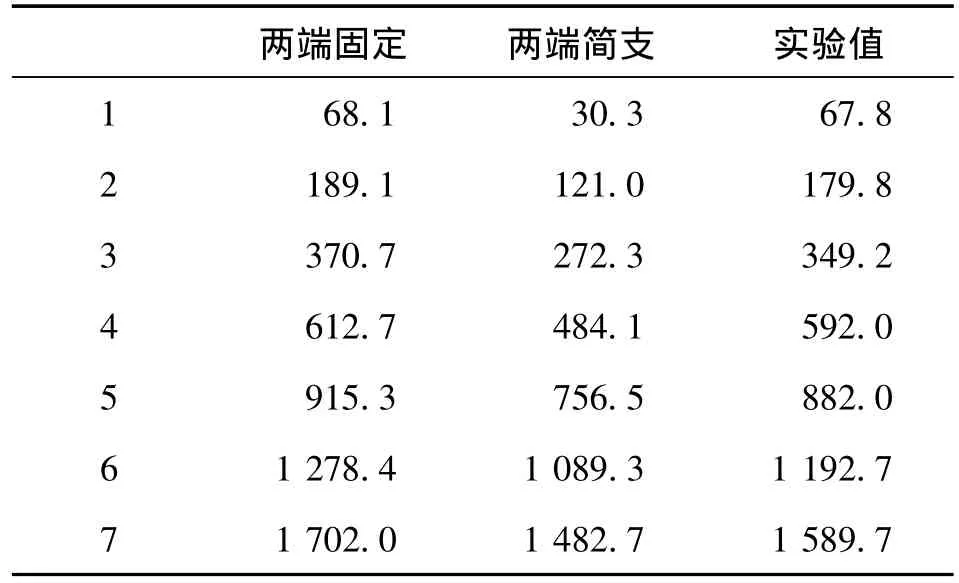
表1 實驗梁前9階固有頻率(Hz)

表2 PVDF傳感器的物理參數

實驗中，用一懸掛激振器作為外部力源位于xd處，通過PCB力傳感器(型號:208A04)測量輸入力，B＆K Pulse動態分析儀進行正弦掃頻(Sweep-Sine)，通過功率放大器驅動激勵器，頻率范圍從5 Hz到2 000 Hz。首先外部力源位于xd=125 mm處，測量輸入力和PVDF薄膜的傳遞函數G(ω)。并把梁均勻分成25個測量點，通過加速度計(型號:PCB333B31)逐點測量輸入力和各測量點位移之間的傳遞函數 H(ω)。把式(1)進行離散化[5，8]，在 xd位置下幅值1 N的點力激勵時的體積位移可表示為:

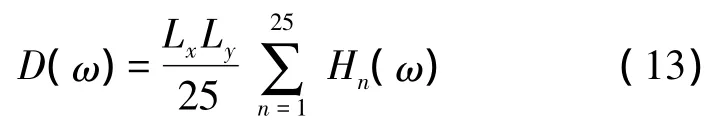
把測量的PVDF傳遞函數G(ω)和通過式(13)計算得到的體積位移D(ω)代入式(12)，可以得到PVDF陣列的加權系數W。圖4表示根據式(12)得到的PVDF加權系數直方圖。圖5表示通過加速度計測量得到的體積位移與通過PVDF陣列得到的實驗結果比較。從圖5可以發現，體積位移在偶數階(2，4和6)模態均出現較大的峰值，這表明實驗中梁兩端的邊界條件并非簡單固定或簡支。這意味著本文的PVDF陣列設計方法可用于任意邊界下振動梁體積位移的測量。

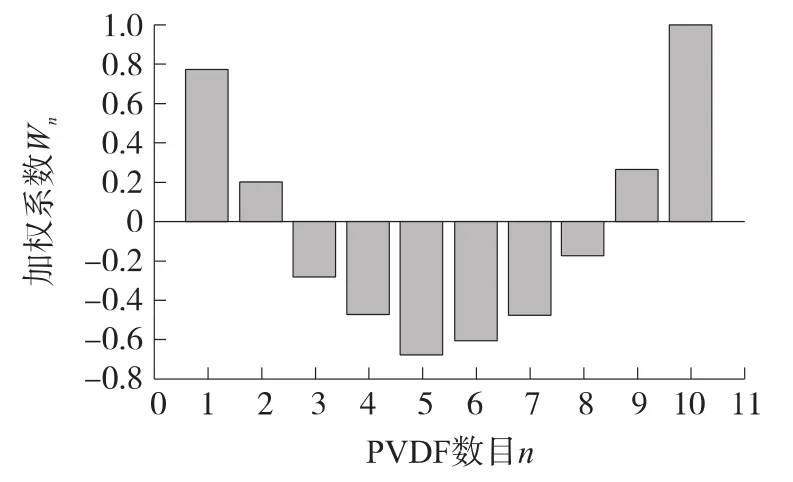
圖4 PVDF傳感器的加權系數Wn

圖5 分別通過PVDF陣列和加速度計測量體積位移幅值和相位(激勵力位于xd=125 mm)

由于PVDF陣列的加權系數與外激勵力性質(如激勵力類型、頻率以及位置等)無關[8－11]，所以可以通過該加權系數通過式(4)計算任意激勵下體積位移。圖6表示當激勵力移動到xd=330 mm時，通過圖4所示的PVDF加權系數得到的體積位移與實際體積位移(通過加速度計測量得到)之間的比較。從圖5和圖6中可以發現，在大部分頻率范圍內，PVDF陣列輸出與加速度計測量的體積位移吻合得很好。與作者之前通過模態方法結合PVDF陣列實驗測量的聲輻射模態[7，9](第一階聲輻射模態幅值與體積位移成正比)相比，本文PVDF陣列的實驗精度大為提高。這是由于模態方法必須預先知道實驗梁的模態信息，但是實驗中梁的邊界條件與理想情況(一般假設為簡支或固定)會有一定誤差。這些邊界條件的誤差會導致PVDF傳感器的測量誤差就隨著頻率提高而增加[14－16]。而本文直接通過偽逆方法結合Tikhonov正則化設計PVDF陣列體積位移傳感器，不需要振動結構任何模態或邊界條件信息。從而使得本文的PVDF加權系數以及測量結果更加精確。

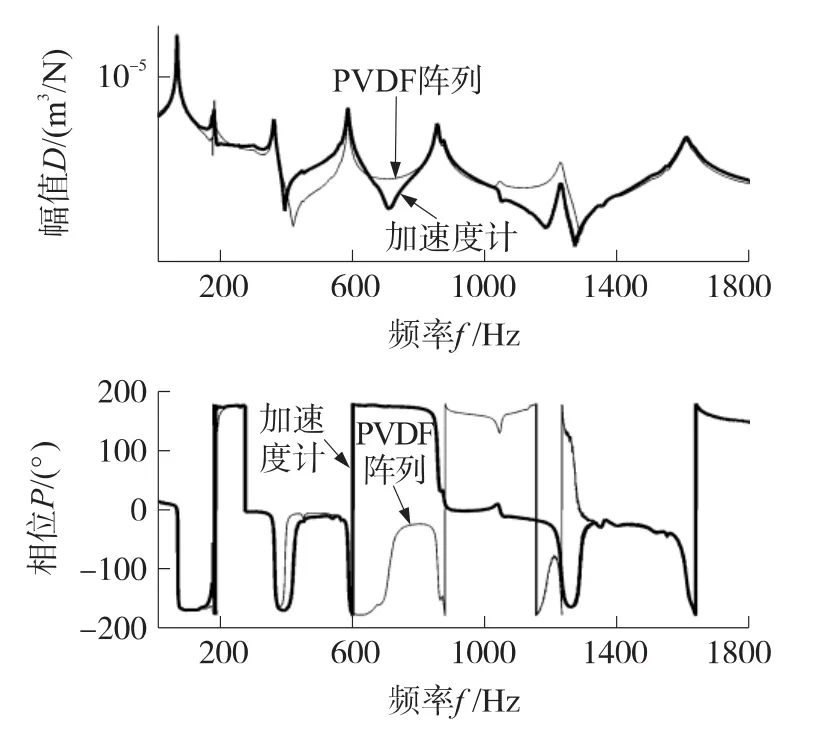
圖6 分別通過PVDF陣列和加速度計測量體積位移幅值和相位(激勵力位于xd=330 mm)

4 結束語

本文通過一組矩形PVDF薄膜測量未知邊界條件下振動梁的體積位移。這種方法的優點在于只需要測量一組在某一激勵力下PVDF陣列的頻率響應函數以及在該激勵力下的體積位移，就可以通過偽逆方法結合Tikhonov正則化得到PVDF陣列的加權系數，該PVDF加權系數可用于計算任意激勵下的體積位移。本文方法的另一個重要優點是不需要任何模態信息或邊界條件信息。實驗結果表明本文方法的測量精度比模態方法[9－13]大為提高。

參考文獻:

[1]Gardonio P，Lee Y S，Elliott J S.Analysis and Measurement of a Matched Volume Velocity Sensor and Uniform Force Actuator for Active Structural Acoustic Control[J].Journal of the Acoustical Society of America，2001，110(6):3025－3031.

[2]Henrioulle H，Sas P.Experimental Validation of a Collocated PVDF Volume Velocity Sensor/actuator Pair[J].Journal of Sound and Vibration，2003，265(13):489－506.

[3]毛崎波，姜哲.通過壓電式傳感器進行簡支梁聲輻射有源控制[J].聲學學報，2001，26(6):527－531.

[4]毛崎波，徐柏齡.通過壓電高分子薄膜設計聲輻射模態傳感器[J].聲學學報，2003，28(3):262－266.

[5]陳衛東，董艷茹，朱奇光，等.基于PVDF的三維機器人觸覺傳感器有限元分析[J].傳感技術學報，2010.23(3):336－340.

[6]揭琳鋒，朱曉鋒，王國林，等.PVDF的大拉伸變形測試機理研究[J].傳感技術學報，2010.23(6):896－898.

[7]Marcellin B Z，Naghshineh K，Kamman J W.Narrow Band Active Control of Sound Radiated from a Baffled Beam Using Local Volume Displacement Minimization[J].Applied Acoustics，2001，62(1):47－64.

[8]Zahui M，Wendt R.Development of Local Volume Displacement Sensors for Vibrating Plates[J].Journal of the Acoustical Society of America，2004，116(4):2111－2117.

[9]Mao Q，Xu B，Jiang Z，et al.A Piezoelectric Array for Sensing Radiation Modes[J].Applied Acoustics，2003，64:669－680.

[10]Mao Q，Pietrzko S.Measurements of Local Volume Displacement Using a Piezoelectric Array[J].Acta Acustica united with Acustica，2006，92(4):556－566.

[11]毛崎波，蔡憶昔，李小華.通過壓電式傳感器陣列測量簡支梁的聲輻射模態[J].中國機械工程，2009，20(9):1169－1172.

[12]Francois A，Man P D，Preumont A.Piezoelectric Array Sensing of Volume Displacement:A Hardware Demonstration[J].Journal of Sound and Vibration，2001;244(3):395－405.

[13]Preumont A，Francois A，Man P D，et al.Spatial Filters in Structural Control[J].Journal of Sound and Vibration，2003，265(1):61－79.

[14]Mao Q，Pietrzko S.Design of Shaped Piezoelectric Modal Sensor for Beam with Arbitrary Boundary Conditions by Using Adomian Decomposition Method[J].Journal of Sound and Vibration，2010，329:2068－2082.

[15]Mao Q.Design of Shaped Piezoelectric Modal Sensors for Cantilever Beams with Intermediate Support by Using Differential Transformation Method[J].Applied Acoustics，2012，73(2):144－149.

[16]Mao Q，Pietrzko S.Design of Shaped Piezoelectric Modal Sensor for a Type of Non-Uniform Beams Using Adomian-Modified Decomposition Method[J].Journal of Intelligent Material Systems and Structures，2011，22(2):149－159.

[17]Berry A.Advanced Sensing Strategies for the Active Control of Vibration and Structural Radiation[J].Noise Control Engineering Journal，2001，49(1):54－65.

[18]Lee C K，Moon F C.Modal Sensors/Actuator[J].Journal of Applied Mechanics，1990，57(2):434－441.

[19]Nelson P A，Yoon S H.Estimation of Acoustic Source Strength by Inverse Methods:Part 1，Conditioning of the Inverse Problem[J].Journal of Sound and Vibration，2000，233(4):643－668.

[20]Yoon S H，Nelson P A.Estimation of Acoustic Source Strength by Inverse Methods:Part 2，Experimental Investigation of Methods for Choosing Regularization Parameters[J].Journal of Sound and Vibration，2000，233(4):669－705.

[21]Yoon S H，Nelson P A.A Method for the Efficient Construction of Acoustic Pressure Cross-Spectral Matrices[J].Journal of Sound and Vibration，2000;233(5):897－920.