模糊參數(shù)自適應(yīng)自整定的逆變電源系統(tǒng)研究

金 平， 尚 凱

（1.中國商用飛機(jī)上海飛機(jī)設(shè)計(jì)研究院 上海 200232；

2.西北工業(yè)大學(xué) 無人機(jī)特種技術(shù)重點(diǎn)實(shí)驗(yàn)室，陜西 西安 710065）

隨著正弦波脈寬調(diào)制（SPWM）逆變技術(shù)的日益成熟，逆變電源被廣泛應(yīng)用到微波通訊、野外活動(dòng)、高速公路、海島、軍事、醫(yī)療、航空航天等各個(gè)領(lǐng)域。逆變電源的負(fù)載可能具有不同的性質(zhì)，如阻性負(fù)載、感性負(fù)載和整流型負(fù)載等，當(dāng)某一負(fù)載投入運(yùn)行時(shí)，特別是非線性負(fù)載，很可能引起逆變器的輸出電壓波形周期性畸變，諧波增加。諧波對(duì)供電系統(tǒng)的污染日益嚴(yán)重，它對(duì)各種電氣設(shè)備都有不同程度的影響和危害[1]。因此逆變電源需要向各種負(fù)載提供高質(zhì)量的電能，也就顯示出了逆變器輸出波形控制的重要性。

逆變電源的控制有多種方案，如閉環(huán)控制[2]，重復(fù)控制[3]，無差派控制[4]和模糊控制[5]等。其中模糊控制器以其不需要被控對(duì)象的精確數(shù)學(xué)模型，較強(qiáng)的魯棒性和自適應(yīng)能力，查找模糊控制表只需要占用處理器很少的時(shí)間等優(yōu)點(diǎn)，因而可以采用較高采樣率來補(bǔ)償模糊控制規(guī)則和實(shí)際經(jīng)驗(yàn)的偏差。文中正是基于模糊控制的原理提出了一套逆變電源的自適應(yīng)自整定控制方法，并通過SIMULINK仿真實(shí)現(xiàn)了逆變電源電路模型的建立、模糊推理運(yùn)算、自整定和自適應(yīng)的功能，利用powergui模塊測量了總諧波含量，驗(yàn)證了該方法的可行性和優(yōu)越性。

1 逆變電源自適應(yīng)自整定控制系統(tǒng)模型

模糊自適應(yīng)自整定控制器結(jié)合了自適應(yīng)和自整定的功能，所以該新型控制器的模糊參數(shù)自整定控制器用來在線整定Kp的大小，模糊參數(shù)自適應(yīng)控制器用來在線自適應(yīng)比例因子的大小[6]。基于這些分析，文中設(shè)計(jì)了該新型控制器的原理框圖，如圖1所示。

MATLAB作為一種開放的編程語言，提供了多種用戶擴(kuò)展工具，相繼推出的建模可視化功能SIMULINK和工具箱為控制系統(tǒng)仿真和設(shè)計(jì)提供了有力的工具。MATLAB為電力系統(tǒng)仿真設(shè)計(jì)了電力系統(tǒng)模塊集，用其中的元件可以方便搭建較為精確的逆變控制系統(tǒng)的仿真模型。

自整定控制器整定Kp，自適應(yīng)控制器對(duì)于自整定控制器的比例因子進(jìn)行在線調(diào)整。誤差e和它的導(dǎo)數(shù)ec作為這兩個(gè)二維模糊控制器的輸入，經(jīng)過設(shè)置好相應(yīng)的模糊規(guī)則推理后進(jìn)行輸出。自整定控制器輸出結(jié)果和自適應(yīng)控制器輸出結(jié)果相乘后作為反饋結(jié)果信號(hào)。這樣就實(shí)現(xiàn)了對(duì)于逆變電源Kp參數(shù)的在線模糊自整定自適應(yīng)控制。

2 模糊控制器參數(shù)的設(shè)置

在系統(tǒng)控制過程中，比例因子對(duì)系統(tǒng)控制性能和穩(wěn)定性影響最為明顯，尤其表現(xiàn)在系統(tǒng)初始運(yùn)行階段。從手動(dòng)控制經(jīng)驗(yàn)看也是如此，操作者主要是根據(jù)誤差和誤差變化，以及系統(tǒng)的控制性能指標(biāo)來調(diào)整控制器的輸出增益，即比例因子的大小，以達(dá)到理想的控制效果。比例因子自整定模糊控制器就是基于這種思路而產(chǎn)生的。

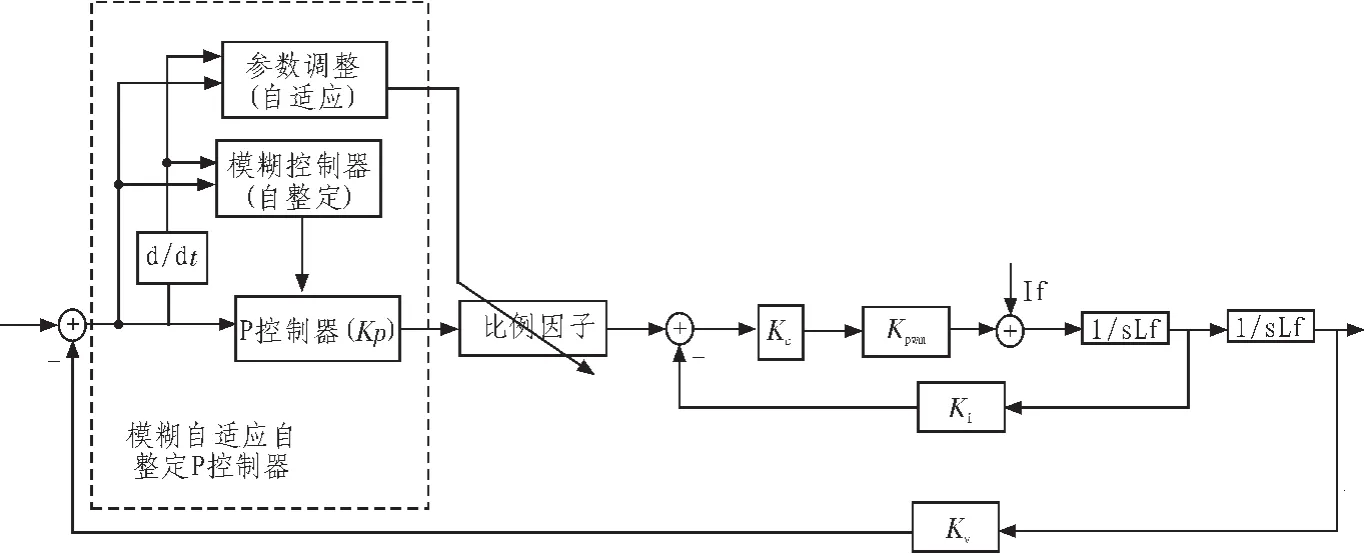
圖1 模糊自適應(yīng)自整定控制器原理框圖Fig.1 Adaptive fuzzy self-tuning controller block diagram

所采用的自整定模塊控制器和自適應(yīng)模塊控制器的輸入輸出隸屬度函數(shù)均采用七段標(biāo)準(zhǔn)高斯分布函數(shù)，模糊規(guī)則排列方式也相同，差別僅在于分布區(qū)間不同。以自整定控制器模糊規(guī)則圖為例說明所有模糊控制器參數(shù)的設(shè)置，如圖2所示。

圖2 自整定控制器模糊規(guī)則圖（輸入和輸出）Fig.2 Self-tuning controller fuzzy rules（Input and Output）

自整定控制器的輸入輸出規(guī)則和區(qū)間分布均相同，按照{(diào)NB，NM，NS，ZO，PS，PM，PB}順序排列。自適應(yīng)控制器模糊規(guī)則圖的輸入?yún)^(qū)間為[-1，1]，輸出區(qū)間為[0.5，1.5]，排列方式和與圖2所示相同。

3 仿真實(shí)驗(yàn)及波形結(jié)果

仿真實(shí)驗(yàn)是通過MATLAB/SIMULINK進(jìn)行的。其中幅值較大的為仿真電壓波形，幅值較小的為仿真電流波形。通過FFT analysis可以直觀的看到對(duì)應(yīng)仿真波形的總諧波失真（Total Harmonic Distortion， THD）。

3.1 阻性負(fù)載 R=10Ω

此處實(shí)現(xiàn)的逆變電源[7]系統(tǒng)性能為輸入單相交流電壓220 V，頻率50 Hz；輸出交流電壓115 V（有效值115 V，峰值163 V），頻率400 Hz。在圖3所示的輸出波形圖中，幅值高的為輸出電壓波形，幅值低的為輸出電流波形。由圖可得，自適應(yīng)自整定控制器阻性負(fù)載啟動(dòng)調(diào)節(jié)時(shí)間僅為2個(gè)周期左右，而且?guī)缀鯚o超調(diào)；圖4所示的阻性負(fù)載輸出電壓的THD值僅為0.34%，遠(yuǎn)小于一般的要求。阻性負(fù)載的突減/突加負(fù)載波形十分完美，因篇幅所限，阻性負(fù)載突減/突加負(fù)載波形圖略去。

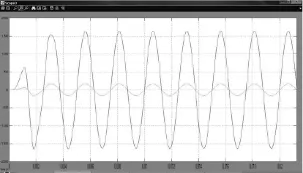
圖3 帶載啟動(dòng)電壓波形圖Fig.3 Load to start the voltage waveforms

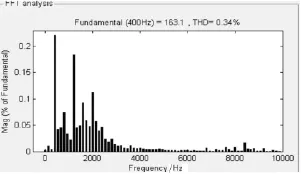
圖4 阻性負(fù)載輸出電壓THD值Fig.4 Resistive load output voltage THD value

3.2 非線性負(fù)載（整流橋負(fù)載）

將整流橋負(fù)載加至逆變器輸出端，并進(jìn)行仿真實(shí)驗(yàn)。由SIMULINK仿真結(jié)果可看出，自適應(yīng)自整定控制器帶整流橋負(fù)載啟動(dòng)時(shí)間僅為2個(gè)周期左右如圖5所示，幾乎無超調(diào)；非線性負(fù)載輸出電壓的THD值僅為0.38%，遠(yuǎn)小于一般的要求如圖6所示。

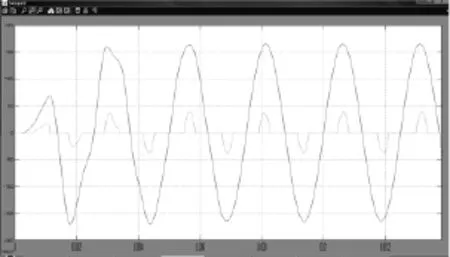
圖5 整流橋負(fù)載啟動(dòng)電壓波形Fig.5 Bridge rectifier load to start the voltage waveform

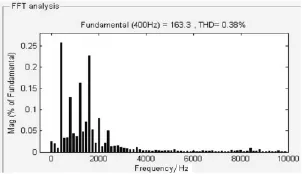
圖6 整流橋負(fù)載輸出電壓THD值Fig.6 Bridge rectifier load output voltage THD value

由圖7所示的突減整流橋負(fù)載和圖8所示的突加整流橋負(fù)載可看出，該新型控制器對(duì)于突變整流橋負(fù)載具有十分優(yōu)越的波形。從（圖3～圖8）仿真圖形結(jié)果可以看出，無論是線性負(fù)載還是非線性負(fù)載，無論是啟動(dòng)波形還是突變負(fù)載波形，該新型自適應(yīng)自整定控制器超調(diào)量小，調(diào)節(jié)時(shí)間短，突加突減負(fù)載輸出電壓波形幾乎不變化，性能十分優(yōu)越。

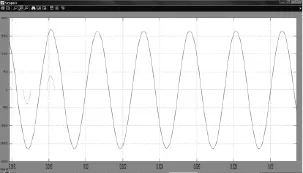
圖7 整流橋突減負(fù)載電壓波形Fig.7 Rectifier bridge suddenly reduce the load voltage waveform

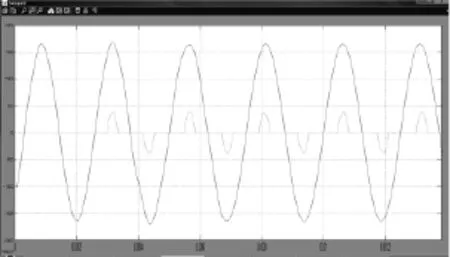
圖8 整流橋突加負(fù)載電壓波形Fig.8 Rectifier bridge suddenly increase the load voltage waveform

4 結(jié) 論

文中針對(duì)逆變電源系統(tǒng)提出了一種全新的模糊參數(shù)自整定自適應(yīng)控制系統(tǒng)。從仿真結(jié)果可以看出，這種新的控制方法的引入，既可以實(shí)時(shí)修改系統(tǒng)的Kp，又可以修改比例因子，從兩方面同時(shí)使系統(tǒng)獲得十分優(yōu)良的動(dòng)態(tài)性能。其快速的響應(yīng)速度和較強(qiáng)的魯棒性說明這種自整定自適應(yīng)模糊控制是一種具有實(shí)用價(jià)值的控制方案，完全能夠逆變電源苛刻的精度要求，對(duì)相關(guān)工程技術(shù)人員有很好地參考價(jià)值。

[1]劉鳳君.正弦波逆變器[M].北京:科學(xué)出版社，2002.

[2]Kawamura A，Yokoyama T.Comparison of five different approaches for real time digital feedback control of PWM inverter[J].IEEE IAS，1990:1005－1011.

[3]李翠艷，張東純，莊硅義.重復(fù)控制綜述[J].電機(jī)與控制學(xué)報(bào)，2005，9（1）:37－44.LI Cui-yan，ZHANG Dong-chun，ZHUANG Gui-yi.Repetitive control-a survey[J].Electric Machines and Control，2005，9（1）:37－44.

[4]郭衛(wèi)農(nóng)，段善旭，康勇，等.電壓型逆變器的無差拍控制技術(shù)研究[J].華中理工大學(xué)學(xué)報(bào)，2000，28（6）:30－33 GUO Wei-nong，DUAN Shan-xu，KANG Yong，et al.The deadbeat control of PWM VSI[J].Journal of Huazhong University of Science and Technology，2000，28（6）:30－33.

[5]李士勇，模糊控制.神經(jīng)控制和智能控制[M].哈爾濱：哈爾濱工業(yè)大學(xué)出版社，1998.

[6]馬長華，朱偉興.比例因子對(duì)模糊控制器動(dòng)態(tài)性能的影響[J].江蘇理工大學(xué)學(xué)報(bào)：自然科學(xué)版，2000，21（5）:87－90.MA Chang-hua，ZHU Wei-xing.Scale factor on the dynamic performance of the fuzzy controller[J].Journal of Jiangsu University of Science and Technology，2000，21（5）:87－90.

[7]劉輝，韓如成，智澤英.基于同倫算法的逆變電源特定消諧法的研究[J].現(xiàn)代電子技術(shù)，2009（8）：173－177.LIU Hui，HAN Ru-cheng，ZHI Ze-ying.Homotopy-based Research on Harmonic Elimination Model in PWM Inverter[J].Modern Electronics Technique，2009（8）：173－177.