無線網絡信號模型的自回歸參數估計

□韓 睿,來曉東

( 1.山西職業技術學院，山西 太原 030009;2.山西廣播電視大學，山西 太原 030027)

1.瞬時頻率

自回歸建模方法已廣泛用于語音處理和高分辨率的信號譜估計領域中。基于的AR模型技術已被證明[1]可以用于區域級/ NAMPS信號的解調，我們的工作就是將該項技術擴展到正被廣泛應用在多種無線通訊系統中的GMSK信號上。分布參數或分布律具有時間依賴性的信號被稱為非平穩信號。瞬時頻率在非平穩信號分析中是一個非常重要的物理量，在許多信號處理的實際應用領域中瞬時頻率估計占有著非常重要的地位。所有靜止的信號都可以表示為特定頻率的正弦和余弦的總和。 然而，對于非平穩信號，例如Chirp信號，這是不成立的，因為信號掃描頻率超過了波段頻率的觀察時間間隔。 通常處理這一問題的辦法是使觀察間隔盡可能小，信號可以被假定為一個正弦波(假設為單組分信號)。如果數據記錄的可用IF估計將非常小，那么就引出了我們將在下面要討論的頻率分辨率的問題。信號可以用以下形式表示：

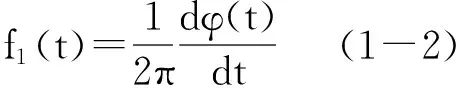
即瞬時頻率是相位對時間的導數[2]。需要注意的是，如果頻率fi(t)為常數時，公式(1-1)可簡化為：

s(t)=acos[2πft+θ] (1-3)

通常中頻通信信號是由一個頻率固定的分量(即載波)和一個隨時間變化的分量構成的，該分量中包含了所要傳送的信息。如果振幅a或相位θ的調制方式分別為隨時間變化的振幅調制和相位調制時，信號可表示為：

瞬時頻率的公式為： f1(t)=fe+fm(t) (1-5)

其中，fc是頻率恒定的載波部分和fm是信息承載部分。

2.頻譜估計技術

自回歸移動平均模型(ARMA模型)是最常用的有理轉移函數模型，并可以由下面的差分方程表示：

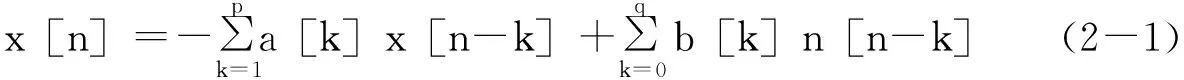
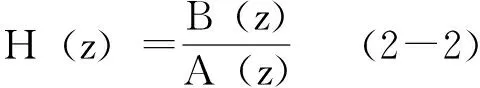
該輸出序列的功率譜密度(PSD)是：

需要注意的是，u[n]是一個在模型中包含的固定部分，不應與觀測噪聲混淆。ARMA模型也被稱為零極點模型。如果我們使MA模型中除a[0]外的所有分母系數都等于零。我們的MA模型的差分方程(2-1)將簡化為：

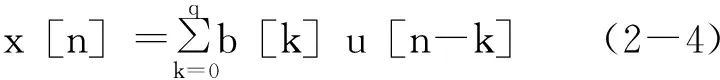
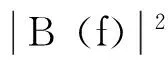
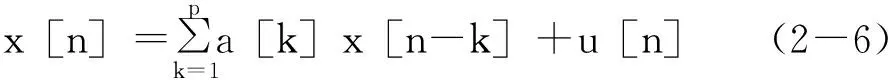
我們假定了a[0]=b[0]=1。如果數據是由純正弦波構成的，那么AR模型通常是最好的選擇。這是因為極點AR模型能準確表示頻率域中的離散信息。

3.模式選擇

信號譜估計模型的選擇過程有三個步驟，如圖1-1所示。第一步是選擇一個具有先驗信息數據資料的基本模型。 我們知道，信號是一個非穩定的調頻信號，即信號的頻率是隨時間變化的，但在小型觀測窗口中，信號可以被認為是穩定的。所以信號基本上會包含一個較完整的噪聲正弦曲線。

圖1-1基于模型的譜估計步驟

即在同信道干擾中將存在有一個以上的正弦分量。因此，選擇的應該是能夠準確代表正弦分量并同時具備一個較高的頻率分辨率的模型。 由上述規定的要求可以很明顯得出結論，AR模型將是最適當的選擇。經典技術無法為客戶提供高頻率分辨率和窄帶程序模型[5]。在模型的選擇中，MA模型或ARMA的優先級順序比AR模型要低。AR模型已被廣泛應用在許多信號處理的領域。它已被證明AR模型可以用來精確地表示AMPS / NAMPS信號，并能夠提供比傳統正交解調器的更好的性能增益。另一個選擇AR模型的原因是，我們可以利用它來進行更有效率的計算，這種方法與傳統的非相干解調技術有緊密的相似性。然后，我們選擇數據模型的下一個步驟就是確定模型參數，一個模型的最佳階數為L=3N/4，這也就是我們在模擬中最常用的參數。在確定模型參數之后，即可將這些參數代入模型以獲取AR譜估計。由(2-6)和(2-7)給出的AR模型，可以用圖 1-2中顯示的IIR濾波器來表示。在這里，模型可以由驅動噪聲序列u [n]和參數a1,a2,……ap來完全定義。

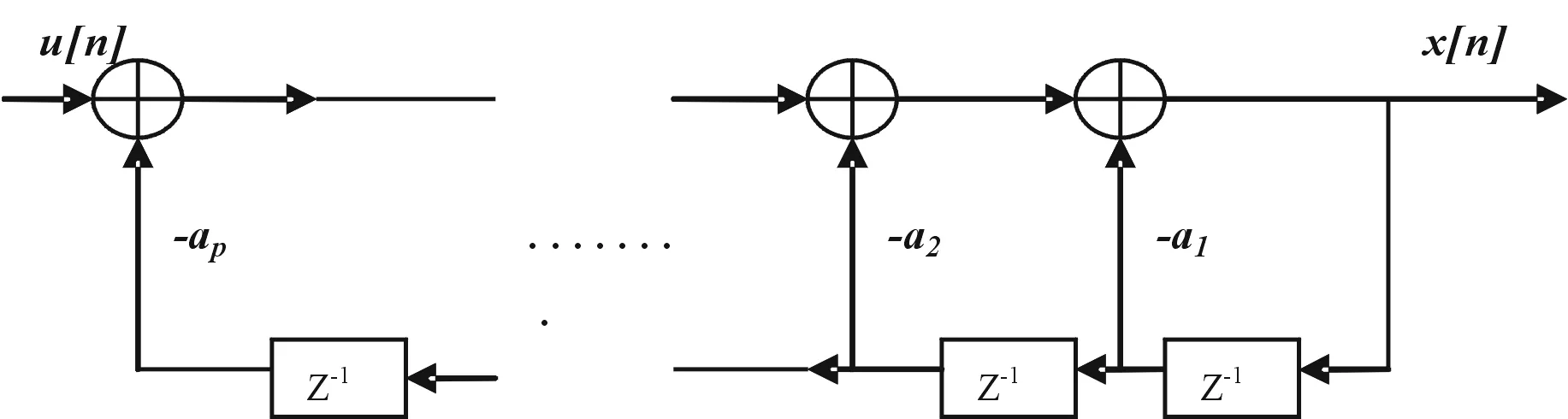
圖1-2 AR模型信號流程圖

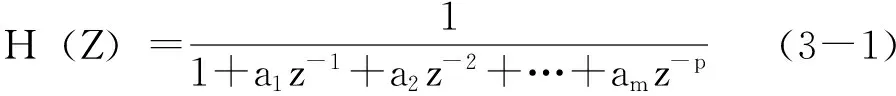
在確定AR模型的線性預測系數參數時，線性預測方程可寫為

其中，{a1,a2,……ap}是預測系數，而預測誤差則為：

濾波器的輸出可以表示為：

z[n]=ejφ[n+1]ejφ[n]=ejφ[n+1]-φ[n](3-4)

對于一個一階濾波器的線性預測方程可表示為：

x[n-1]a[1=-x[n] (3-5)

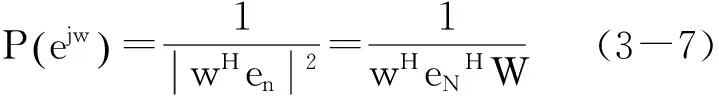
這就是所謂的偽譜，因為它只提供了有關信息的位置復指數，而不是他們的權。該方法可以消去音頻信號的最主要的相關性限制矩陣。偽譜可定義為：

其中噪聲E是指噪聲特征向量矩陣：

Enoise= [eM+1eM+2… eN] (3-9)

假設復雜的指數函數M的數量是已知的。因此，特征向量數目是大于復指數的數量。該特征值對應的最小特征值和噪音是由特征向量定義的，它是正交的信號載體。

ESPRIT是一個比較新的子空間技術，提供了大幅提高頻率分辨率的解決方案。原來的ESPRIT算法，提出了在該方案框架下的相關數據矩陣，但存在有嚴重的數值問題。最小二乘法(LS)和總體最小二乘法(TLS)是用來解決這些問題首選方法。 ESPRIT算法的子空間方法與其他方法不同，它進行頻率估計時使用的是離散信號子空間，而不是噪音子空間。這種方法的關鍵是要分成兩個信號交錯子的空間。讓我們定義一個信號矩陣S為：

然后兩個矩陣 S1、S2是分別消除第一行和最后一行的剩余部分。

這兩個矩陣是相關的: S2=S1Φ (3-10)那么

顯然，矩陣 包含的頻率信息。如果S1和S2為已知，則 很容易使用最小二乘法。

4.模擬結果

在測試中，我們使用LTE-YD-02B1移動通信系統綜合實驗箱系統中的基帶成形模塊，產生PN31偽隨機序列作為信源；將基帶信號進行串并轉換；按QPSK、OQPSK、MSK、GMSK調制要求進行基帶成形，形成測試信號。并采用 Matlab 編程,生成最終的測試結果。

在比較時選擇的信號是高斯濾波的帶寬為3dB ，BT= 0.5 的MSK(GMSK調制)信號。我們使用復雜基帶模型進行了模擬，采樣頻率fs=20。對于在AWGN信道下的基于模型的解調器的執行情況使用主成分分析法(PCM)的結果如圖2-1 - 2-3所示(規定信噪比為30dB)。

當存在同信道干擾的情況下，基于模型的設計(MBD)的性能如圖2-1所示。同時，限幅鑒別頻器(LD)的表現也顯示出來以供參考。可以看出，在具有獨立的過濾器的長度L或數據樣本數N的情況下，MBD和LD具有相同的誤碼率性能。但是，MBD與LD在不同的相位差下的表現則不具備相關性。接下來，我們對MBD測試實例進行評估。我們采用LMS算法來跟蹤濾波器的系數，而不是為每一個系數進行單獨的計算。我們將步長設置為0.005，結果發現迭代次數為10時，LMS算法足以減少預測誤差。而再進一步的迭代則無法繼續提高誤碼率性能。從結果中可以看出，如果濾波器的階數大于3，在性能上就會有明顯的降低。

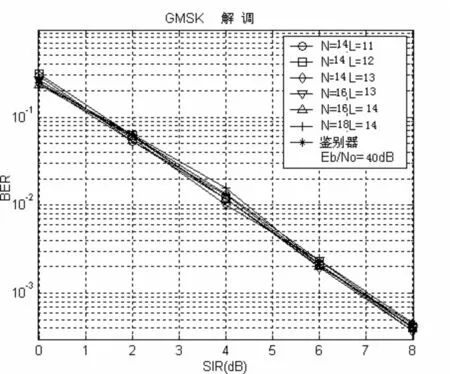
圖2-1 LD和基于模型的解調器在各種濾波器長度下的性能表現

如果有一個單列的正弦分量信號，那么第一個角度的系數就可以用于頻率估計。事實上，如果信號具有足夠的過采樣，且所有過濾系數都具有相似的值和正弦分量，那么我們就可以通過角度來確定任何一個相關系數。所有上述測試方案的性能比較如圖2-2所示。最后我們在瑞利衰落環境中對MBD的性能進行評估。可以看出，MBD與LD的表現相似，衰落是緩慢的并且是與頻率不相關的。我們設置了兩個極端的情況：一是兩種信號經歷了完全不相關的衰落。二是兩種信號經歷了相同的衰落。可以看出，在不相關衰落的情況下，其性能更差。在第二種信號經歷了相同的衰落情況下，性能主要由兩個信號的相對強度來決定。在實際運行環境中，兩個信號所經歷的衰落與性能表現將會介于兩個極端情況之間。

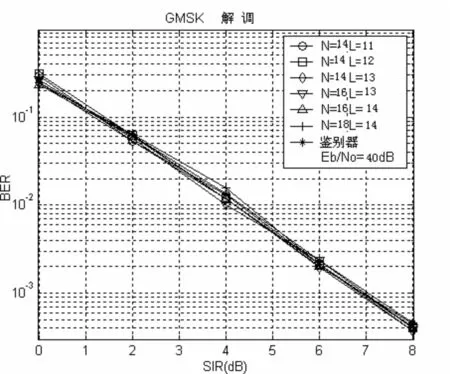
圖2-2 以各種模型為基礎的解調方案的性能比較

5.結語

我們在自回歸模型的基礎上，針對中頻信號的特性提出了高頻率分辨率的要求。然后討論了AR模型參數的確定問題，我們采用了最小二乘法來確定AR參數，這種方法的優點在于它是直接應用于數據而無需對自相關函數求解。同時，我們選用LMS算法來跟蹤濾波器的系數，以免于對每一個系數進行單獨的計算。而AR模型的譜估計可以通過將參數代入到模型中來獲得。模擬結果顯示，基于模型的設計(MBD)與常規的限幅器/鑒頻器在各類環境中進行比較后，總體上并無十分明顯的優勢，只有當載波頻率之差為1/2T時，MBD才會提供較好的性能提升。

：

[1]Boualem Boashash, Estimating and Interpreting the Instantaneous Frequencyof a Signal - Part 1: Fundamentals[J].Proceedings of the IEEE , 1992, 80(4) :2136-2138.

[2]Boualem Boashash, Estimating and Interpreting the Instantaneous Frequency of a Signal - Part 2: Algorithms and Applications[J].Proceedings of the IEEE, 1992, 80(4):566-569.

[3]S. Lawrence Marple Jr. Spectrum Analysis: A ModernPerspective[J].Proceedings of the IEEE, 1981,69(3):1380-1419.

[4]S. Verdu．Multiuser Detection[M].Cambridge University Press, Cambridge，1998：53-66.

[5]Mathew L. Welborn．Co-Channel Interference Rejection Using a Model-Based Demodulator[D]．Virginia Polytechnic Institute, 1995.