“人—船”模型的教學研究

何述平

(西北師范大學教育學院物理教育研究所,甘肅 蘭州 730070)

1 引言

模型方法是物理學的重要研究方法,也是物理問題的基本而有效的解決方法.如何運用模型方法,“人—船”模型具有典型性,且對其已有不少討論［1－5］;但似乎有模糊之處、令人費解之處.若從大學普通物理居高臨下地審視“人—船”模型問題,其物理實質究竟怎樣？中學物理范圍內怎樣合理地解決？有哪些可行的解法？各解法有何特點？本文對此作相應探討,以期疑惑的解釋,提供合理運用模型方法的理論依據,并為“人—船”模型開放探究式的教學設計奠定基礎.

圖1

2 探討

為明晰起見,先簡述“人—船”模型問題,再做兩個層次的細致探討.

2.1“人—船”模型

質量為M、長為L的小船位于湖水上,質量為m的人站在船頭,最初人和船都靜止,如圖1.當人從船頭走到船尾時,小船移動了多少距離？(不計水對船的阻力)

將人、船視為系統,水平方向所受合外力為零,則水平方向動量守恒;以水平向右為正向,sm、sM分別為人、船相對于湖岸的位移大小,如圖1,則有［1］

由(1)～(4)式得

sM即為小船相對湖岸移動的距離.

或在式(1)的基礎上引入平均速度［2］或“平均動量”［3－5］,從而用平均速度表達式(1)、(2)、(3),再結合式(4),得到與式(5)、(6)一致的結果.

2.2 實質探討

式(2)、(3)或用平均速度表達式(1)、(2)、(3)(v、V是瞬時速度),合理否？或許從大學普通物理居高臨下地審視“人—船”模型問題,對明確其實質會更有益.

大學普通物理中可見到的、與“人—船”模型實質相同的有“人—車”模型［6］、“狗—船”模型［7］,且有動量守恒的式(1)和相對位移大小的式(4).由式(1)對時間0～t積分(t為人從船頭走到船尾的時間)得

再結合式(4),得同(5)、(6)的結果(還可運用質心運動定理求解,得相同的結果).

因速度對時間的積分為位移,則無論人、船相對于湖岸做何種直線運動(勻變速、非勻變速直線運動),式(7)在大學普通物理上均成立,即具有一般性.由受力分析、牛頓定律知,人、船的相互作用力即摩擦力,既可是恒力,也可是變力.這樣,人、船相對于湖岸只可能做勻變速或非勻變速直線運動,不可能做勻速直線運動.因此,式(2)、(3)明顯是不合理的［因式(2)、(3)意味著人、船相對于湖岸做勻速直線運動］.

用平均速度表達式(1)、(2)、(3),貌似合理,實則不然.從物理概念看,有平均速度的概念(平均速度是位移與對應時間之比,對應著時間,可理解為等效的勻速的速度),而似乎沒有“平均動量”的概念(動量是狀態量,對應著時刻,動量的時間變化率等于力,動量的增量等于沖量,沖量與對應時間的比為平均力,均有明確的物理意義.然而,動量對時間積分、再取時間平均,從數學形式看好像是“平均動量”,但從物理實質看,動量對時間的積分沒有意義).因此,單獨審視用平均速度表達式(2)、(3),是合理的(位移等于平均速度與時間之積,對應著時間),但若用平均速度表達式(1),則沒有物理意義.而且用平均速度表達式(2)、(3)及式(1)(進而出現了沒有物理意義的“平均動量”)的目的是聯立計算位移,則用平均速度表達式(2)、(3)又顯得不合理.

運用動量守恒定律的意圖是避開所研究問題的系統經歷過程的細節和系統內可能復雜的相互作用,直接考慮系統過程的始末態的動量,從而使問題解決更簡捷［8］.因此,“人—船”模型問題的解決首選運用動量守恒定律.然而,從以上探討知,由動量守恒即式(1)求位移,不得不用積分(目前中學基礎物理不涉及).為了避免積分,想當然地認為有式(2)、(3)或用平均速度表達式(1)、(2)、(3),但這是不合理的.結果的式(5)、(6)卻是合理的.

從能量方面看,對“人—船”模型,人體的化學能通過摩擦力做功轉化為人和船的動能.

2.3 教學探討

中學物理中怎樣合理解決“人—船”模型問題呢？結合中學物理教學的特點,探究、概括出以下4種可行的解法,并作必要的討論.

2.3.1 中學物理的解法

解法1:動量守恒定律＋勻變速直線運動速度規律法.

人、船視為系統,則水平方向動量守恒,有式(1)、(4).人、船間的摩擦力視作恒力,則人、船相對湖岸做勻變速直線運動.依據勻變速直線運動速度規律有(大小關系)

其中t為人從船頭走到船尾的時間,v、V分別是t時刻時人、船的瞬時速度.由式(1)、(4)和式(8)、(9)也得式(5)、(6)的結果.

人、船視為系統,則水平方向動量守恒,有式(1)、(4).人、船間的摩擦力f和f′(水平方向)視作恒力.依據動能定理、牛頓第三定律有(大小關系)

由式(1)、(4)和式(10)～(12)也得式(5)、(6)的結果.

解法3:勻變速直線運動位移規律＋牛頓第二、三定律法.

人、船分別為研究對象,人、船間的摩擦力f和f′(水平方向)視作恒力.人、船相對湖岸做勻變速直線運動.依據勻變速直線運動位移規律、牛頓第二、三定律有(大小關系)

和式(12)、式(4).由式(13)～(16)和式(12)、式(4)也得式(5)、(6)的結果.

解法4:動量守恒定律＋勻變速直線運動速度－位移規律＋牛頓第二、三定律法.

人、船視為系統,則水平方向動量守恒,有式(1)、(4).人、船間的摩擦力f和f′(水平方向)視作恒力,則人、船相對湖岸做勻變速直線運動.依據勻變速直線運動速度－位移規律、牛頓第二、三定律有(大小關系)

和式(15)、(16)、(12).由式(17)、(18)和式(15)、(16)、(12)及式(1)、(4)也得式(5)、(6)的結果.

第三步：在單路徑饋線恢復方案施行后，配電網的初始狀態發生變化，對第二階段主變負載率進行修改，通過MOPSO算法求解數學模型，計算多路徑饋線的最小恢復供電時間以及最大恢復供電能力。

2.3.2 解法的討論

“人—船”模型問題的4種可行解法所運用的物理基本規律如各解法所注,并以此稱謂各解法,構成各解法的中學物理理論依據,作為各解法的特點之一.從處理物理問題基本方法看,4種可行解法都運用了理想化法(理想化對象——質點或質點組即系統,理想化過程——勻變速直線運動)［9］;從物理學方法論看,解法1、2、4運用了綜合—分析法［9］(即系統—隔離法),解法3運用了分析法(即隔離體法);作為各解法的特點之二.

比較“人—船”模型問題的4種可行解法,可知簡捷程度(由簡到繁)依次為解法1、解法2、解法3(此法雖相對較繁,但物理分析透徹、物理過程清晰)、解法4.

3 教學建議

依據2.2、2.3,先給出“人—船”基本模型問題的教學建議,再探討一個“人—船”變形模型問題的實質,并據此提出相應教學建議.

3.1 基本模型的教學建議

對“人—船”基本模型問題,雖然可以根據中學物理的具體教學內容、合理教學目標和可行解法特點,具體選擇開放探究式教學方法,但應將重點放于一題多解,因為這樣才可體現開放與探究,才可多角度進而有效地理解物理基本過程,鞏固、深化、活化物理基本規律,領悟物理基本方法,從而提升分析解決問題的能力,并為變形模型問題的解決奠定良好的基礎.

3.2 變形模型的教學建議

3.2.1 問題探討

某人在靜止于湖水的船上練習射擊,人在船的一端,靶置于船的另一端,槍口到靶的距離為L,船、人、槍、靶的總質量為M,槍內另裝有質量均為m的子彈n顆.發射后一子彈時,前一子彈已嵌入靶中.求全部子彈射入槍靶后,船移動的距離.(不計水對船的阻力)

將子彈與船、人、槍、靶視為系統,每次發射時系統的總動量為零,認為一次發射質量為nm的全部子彈與依次發射質量均為m的n顆子彈等效;然后與“人—船”模型對應得

此解法合理否？憑直覺似乎合理,但具體推理則表明不合理.現詳細推證如下.

第1次發射,將第1顆子彈與n－1顆子彈、船、人、槍、靶視為系統,水平方向不受外力,則系統動量守恒,有

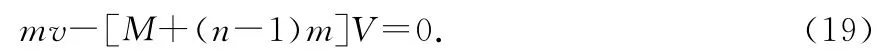
然后,子彈m和n－1顆子彈、船、人、槍、靶［M＋(n－1)m］分別以v和V做勻速直線運動(忽略重力對子彈的作用),則位移大小分別為

其中t為子彈從槍口到射入槍靶的時間.由相對位移大小關系,有

由式(19)～(22)得

對子彈射入槍靶,依據動量守恒有

表明子彈射入槍靶后,系統的總動量為零,相對湖岸的速度均為0.

第2次發射,過程同第1次發射,也有同(19)～(24)的表達式.不難想見,第i次發射,過程也同第1次發射,有(19)～(24)的表達式.因此,第n顆子彈射入槍靶后,船移動的距離為

從能量角度看,彈藥的化學能通過彈藥燃爆產生的力做功轉化為子彈m和n－1顆子彈、船、人、槍、靶［M＋(n－1)m］的動能,然后通過子彈與槍靶間的摩擦力做功轉化為它們的內能.

3.2.2 教學建議

由3.2.1知,導致謬誤的根本原因是物理過程未清晰,盲目對應、籠統“對號入座”.因此,對“人—船”變形模型問題,應突出物理基本過程的分析,因為這樣才可確定能否與“人—船”基本模型對應;若物理基本過程不盡相同,則應考慮變通,因為不同的物理基本過程一般遵循不同的物理基本規律.所以,對“人—船”變形模型問題,雖然也可根據中學物理的具體教學內容、合理教學目標,具體選擇開放探究式教學方法;但應既關注相同與對應,又關注不同與變通,即應將重點放于“對應—變通”.

4 結語

本文的“人—船”基本模型問題和變形模型問題的實質探討,澄清了相應的模糊之處、令人費解之處,明確了物理實質.“人—船”基本模型問題的教學探討,給出了中學物理范圍內合理、可行的4種解法,并討論了解法的特點和簡捷程度.“人—船”基本模型問題和變形模型問題的教學建議,均突出了物理基本過程,因為這是解決物理問題的前提和基礎;并分別就同一物理基本過程運用相同或不同物理基本規律和不同物理基本過程,運用不同物理基本規律提出了一題多解和“對應—變通”的教學建議;而運用不同的物理基本規律一般意味著采用了不同的物理基本方法.因此,對“人—船”模型問題,運用模型方法的程序應是:物理基本過程→物理基本規律→物理基本方法.這應是合理運用模型方法的理論依據之一.

1 閻金鐸,田世昆.中學物理教學概論(第2版).北京:高等教育出版社,2003.151

2 劉炳升.走進高中新課改:物理教師必讀.南京:南京師范大學出版社,2005.149—153

3 陳剛,舒信隆.新編物理教學論.上海:華東師范大學出版社,2006.124—128

4 陳剛.物理教學設計.上海:華東師范大學出版社,2009.144—146

5 陳剛,舒信隆.問題圖式在物理問題解決教學中的應用.課程·教材·教法,2009,29(7):57—61

6 程守洙,江之永,朱詠春.普通物理學(第1冊,第4版).北京:高等教育出版社,1982.80—81

7 惲瑛,朱君哲,舒素珍.哈里德物理學習題解答(第1卷).北京:科學出版社,1985.196—197

8 漆安慎,杜嬋英.力學基礎.北京:高等教育出版社,1982.173

9 張憲魁,李曉林,陰瑞華.物理學方法論.杭州:浙江教育出版社,2007.106,78