艦載雷達電子對抗中對策論分析

曹 輝，聶玉寶，余貴春

（1.海軍指揮學院，南京 210016，2.解放軍92858部隊，南京 210016）

0 引 言

雷達的出現和使用極大地提高了艦艇獲取信息的能力，現代艦載雷達運用先進技術，能短時間內獲取目標大量重要信息，是艦艇主要的預警探測設備。為奪取海戰勝利，雷達方要保證己方雷達正常工作，干擾方需干擾對方雷達設備工作，為此，作戰雙方開展了不斷更新發展的電子對抗。干擾方的干擾手段和雷達方的抗干擾措施都是動態的選擇，而作為研究具有動態對抗性問題的數學理論的對策論應用于這一問題具有一定的實際意義。

1 艦載雷達電子對抗與對策論

艦載雷達電子對抗主要是艦載雷達方與飛機、艦艇上的干擾設備之間的對抗行動，現介紹該問題的提出與對策論基本理論。

1.1 問題的提出

當前，艦載雷達常用的抗干擾技術有捷變頻、副瓣隱匿和寬限窄等。對艦載雷達的干擾技術分為有源干擾和無源干擾，常見的有源干擾技術有阻塞式干擾、掃頻干擾、瞄準式干擾等；副瓣轉發器、距離拖延門、箔條等為無源干擾技術。為研究對策論在艦載雷達電子對抗中的應用，在對艦載雷達干擾設備及雷達性能全面分析的基礎上，結合實際訓練以及未來海戰場可能出現的情況，以單部某型雷達與假想干擾機對抗為例進行說明［1］。

1.2 對策論的基本理論

具有競爭和對抗性質的決策問題稱為對策，一個對策就是對策論對現實世界某個對抗局勢的抽象。因此，艦載雷達與干擾方的對抗決策問題可引入對策論理論。

（1）對策論簡介

對策論亦稱博弈論或競賽論，它既是現代數學的一個分支，又是運籌學的一個重要學科。對策論起源于對博弈的數學研究，其作為一門學科的正式誕生，始于數學家馮·紐曼和摩根斯坦于1944年發表的《對策論和經濟行為》。對策論在利益沖突雙方行動和意圖不完全明了的情況下，能用數學方法得出決策者應采取的最優行動方案。在艦載雷達對抗中引入對策論來分析對抗信息，得出最優對抗策略，以此作為艦載雷達對抗決策的依據［2］。

（2）對策論的重要概念

對策是現實對抗局勢的數學模型。在對策模型中有3個要素：局中人、策略和支付［3］。

局中人，就是參與對抗或競爭的個人或利益集團。在對策中，一個局中人是一個代表本方利益的、有決策權的、理智的決策者。

策略，就是各局中人擁有的可供其選擇采用的行動策略。在對策論中，策略有其特定的含義，一個策略就是局中人在對策中的一套完整的行動方案。

支付，在對策論中是指當各局中人決定了各自策略之后，這些策略組合所導致的對抗結果的數量表示。支付可以是對抗結果的價值，也可以是結果的效用。

從決策的角度看，局中人就是決策者。這里的策略就是雙方（決策）方案，支付就是雙方所得到的決策結果。

（3）對策論要素分析

在對策論中，可以根據各種不同的標準將對策分為不同的對策類型：

（a）根據對策中局中人的個數，可以分為二人對策和多人（N人）對策。

（b）根據各局中人的支付之和是否為一固定的常數，可以分為常和對策和非常和對策；根據各局中人的支付之和是否為零，可以分為零和對策和非零和對策。零和對策是常和對策的一種特例。

（c）根據各局中人的策略數目是否是有限個，可以分為有限對策和無限對策。

對于艦載雷達對抗這個特定的研究對象來說，可以認為這是“二人有限零和”對策。“二人”是雷達方和干擾方；“有限”指干擾方的干擾措施和雷達方的抗干擾措施是有限的；“零和”的意義則為雷達方／干擾方的所得即是干擾方／雷達方的所失。

一個二人有限零和對策的數學模型是：Γ（I，J，U），其中Γ為對策，I為局中人1的策略集合，即：

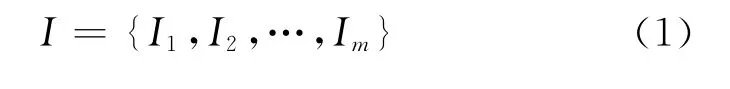
式中：Ii為局中人1的第i個策略，其總的策略數量為m。

J表示局中人2的策略集合，即：

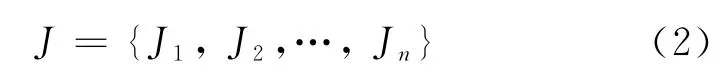
式中：J j為局中人1的第j個策略，其總的策略數量為n。

U表示局中人1的支付矩陣，即：

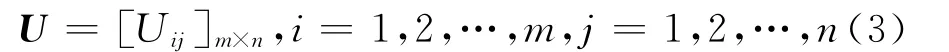
式中：U ij為局中人1采取第i個策略并且局中人2采取第j個策略時，局中人1所得到的支付。

由于局中人2的支付矩陣等于局中人1支付矩陣的負值，因此局中人2的支付矩陣為－U。

（4）對策論的求解

針對單部艦載雷達電子對抗問題所關心的是對抗雙方能否達到一個平衡局勢，分為純策略（有鞍點）和混合策略（無鞍點）2種情況。

（1）一個矩陣對策，如果支付矩陣有：

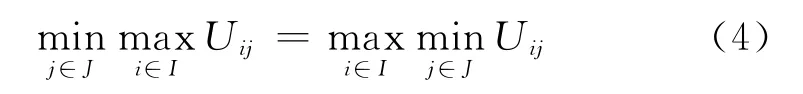
成立，記其值為V，稱為對策的值，使上式成立的局中人1的第i個策略和局中人2的第j個策略，分別是局中人1和局中人2的最優純策略。

（2）一個矩陣對策，當下式成立時：

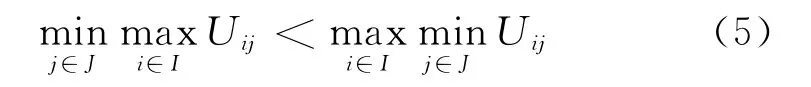
該矩陣不存在鞍點，不存在最優純策略，但存在最優混合策略解。矩陣對策總是存在最優混合策略解，純策略是混合策略的特例。

局中人的一個混合策略，就是該局中人純策略集合上的一個概率分布。局中人1策略集I的概率分布為X＝（X1，X2，…，Xm），局中人2策略集J的概率分布為Y＝（Y1，Y2，…，Y n），這2個混合策略必須滿足

2 對策論在雷達電子對抗中的應用

為了便于綜合分析問題，依據艦載雷達性能，其抗干擾的策略集為［4］：

M＝｛寬限窄，副瓣對消，副瓣隱匿，捷變頻｝

此處假定艦載雷達干擾方的策略集可取為：

N＝｛瞄準，掃描，阻塞，轉發式欺騙，箔條干擾｝

結合艦載雷達與干擾裝備的具體性能參數和對抗雙方的實際情況，例如對抗雙方的天線增益、發射功率、干擾噪聲帶寬、相隔距離等，設定1個固定值，經定量計算和定性分析并且結合相應的干擾效果算法，可得到艦載雷達抗干擾對抗關系矩陣。經分析計算得出的對抗關系矩陣見表1［5］。

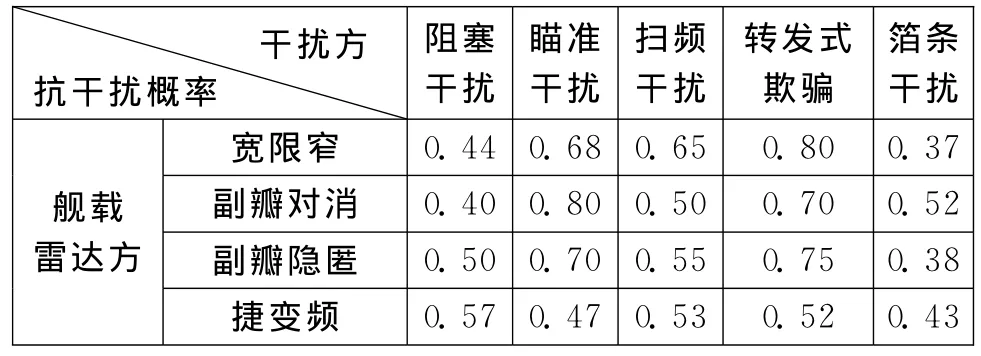
表1 雷達方與干擾方的對抗關系矩陣

通過表1中的數據可看出對抗雙方在純策略情況下，各自所采取的策略進行對抗的得益情況。如在與寬限窄方式的對抗中，箔條干擾條件下抗干擾成功概率為0.37，而抗掃頻干擾條件下抗干擾成功概率為0.65，表明寬窄限對抗掃頻干擾的效果較好，這與實際情況相符，從而證實了數據的可靠性。

由表1就可確定支付矩陣A：

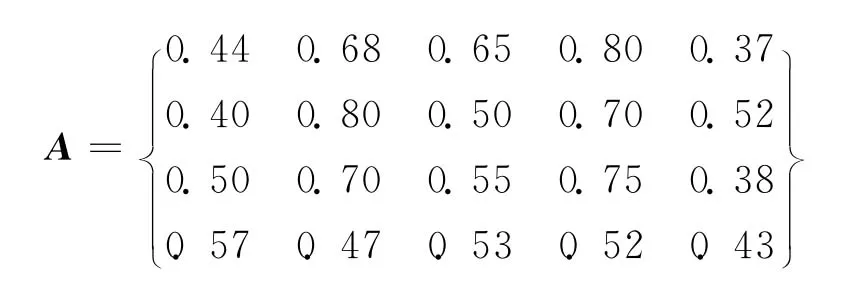
結合取定的M，N，一個完整的對策問題就被描述出來。

矩陣對策有很多成熟的解法，如線性規劃算法、迭代算法等。線性規劃算法是矩陣對策的普適解法，可以用于求解任何矩陣對策，包括有鞍點的矩陣對策；而迭代算法用于求解大型矩陣對策，是最實用、最適于計算機執行的算法。在此利用線性規劃算法進行求解。

根據表1，建立下面2個線性規劃問題。

（1）艦載雷達效用最高的線性規劃問題

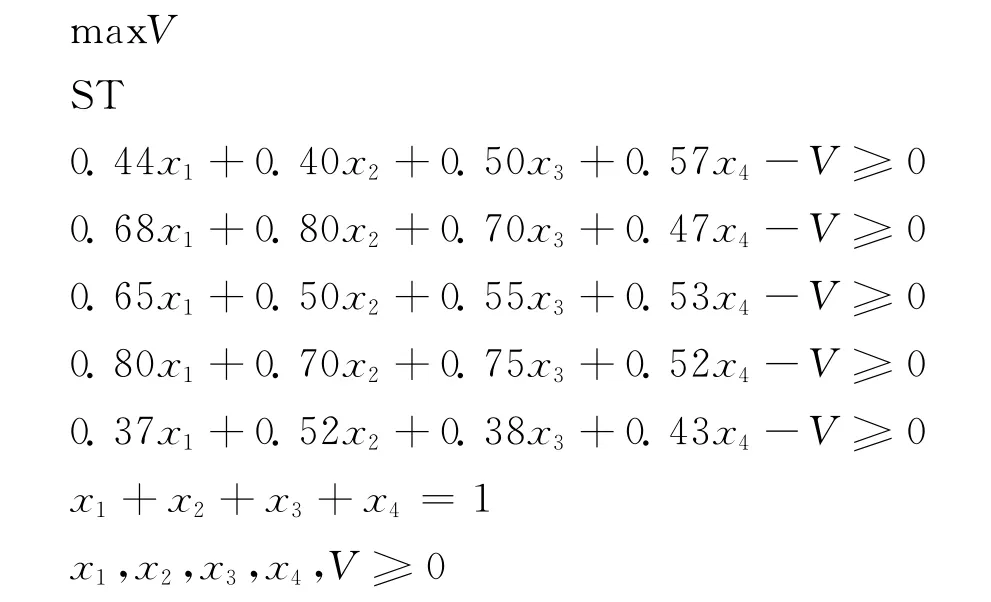
（2）干擾方使艦載雷達效用最低的線性規劃問題

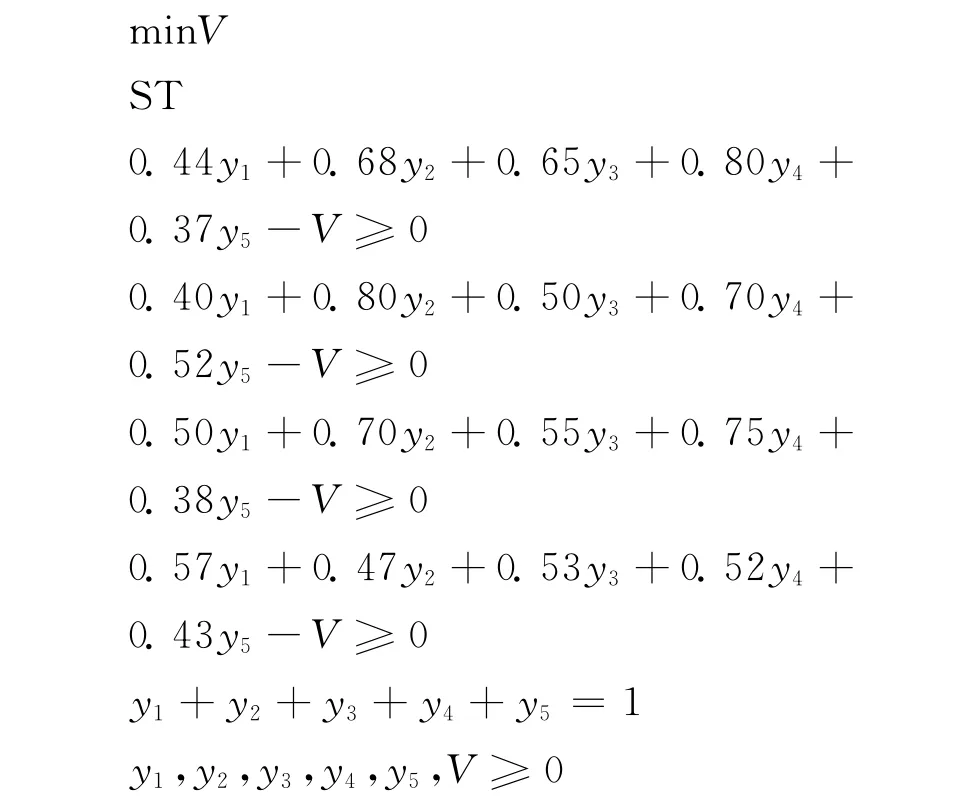
利用線性規劃計算軟件（如LINDO）可以求解得到艦載雷達方與干擾方矩陣對策，結果如表2所示。

表2 雷達方與干擾方對抗的矩陣對策解

從表2中可看出，艦載雷達的最優混合策略是分別以概率0.54和0.46采用副瓣對消和捷變頻選擇方式及零概率采取寬限窄、副瓣隱匿進行抗干擾。而干擾方的最優混合策略是分別以概率0.35和0.65采用阻塞和箔條干擾以及零概率采取瞄準、掃頻、轉發式欺騙干擾的策略來干擾艦載方雷達。得到艦載雷達方與干擾設備對抗中的得益值僅為0.478 5左右。通過數據分析可知，艦載雷達方得益較小的原因是艦載雷達缺乏有效對抗箔條干擾的措施。根據分析結果可知，在海戰中，箔條干擾仍是對抗雷達的有效措施，而為有效提高艦載雷達的對抗性能和在對抗中的收益，可相應地采取抗箔條干擾的措施或者配備多部不同的雷達。

3 結束語

本文分析結果表明，將對策論應用于艦載雷達電子對抗策略分析后，將極大地優化艦載雷達抗干擾方式，為合理地制定艦載雷達抗干擾策略，提高艦載雷達的電子對抗能力有著重要的指導作用。

［1］張克明，王曉亮，王國良.電子對抗新策略矩陣對策［J］.電子對抗技術，2004，19（1）：18－20.

［2］史越冬.指揮決策定量分析［M］.北京：海潮出版社，2008.

［3］李潮，張多林，劉付顯.對策論在雷達電子戰效能評估中的應用［J］.航天電子對抗，2006，23（3）：21－22.

［4］王軍，林強.米慈中，等.雷達手冊［M］.北京：電子工業出版社，2003.

［5］沈鵬，張宏銘，張瑞峰，等.對策論及其在雷達電子對抗中的應用研究［J］.電子對抗，2009（5）：14－16.