一類具擴散的SIR傳染病模型的穩定性分析

朱道宇

（貴州民族大學理學院，貴州貴陽 550025）

一類具擴散的SIR傳染病模型的穩定性分析

朱道宇

（貴州民族大學理學院，貴州貴陽 550025）

研究一類具有空間擴散的SIR傳染病模型，通過討論線性化方程的特征值得到該模型的染病平衡點是局部穩定的，并利用Lyapunov函數得到該平衡點全局漸近穩定的一個充分條件.

傳染病模型；平衡點；漸近穩定

1 引言

目前的很多傳染病模型都源于Kermack和McKendrick在文獻[1]中首次提出的SIR模型，該模型及其各種推廣后的模型的動力學行為已被很多學者進行了深入研究.在生態環境各因素的交互作用中，空間因素是影響生態種群形成和運作的一個重要因素[2-5].在建立生態數學模型時，人們越來越多地意識到空間因素的必要性.從生物學觀點來看，每個生物個體都分布于空間中并與周圍環境以及附近的其他生物個體相互作用.為了尋找食物，躲避更高的傳染風險或者其他目的，個體一般會向種群密度較低的方向擴散，以期有更多的自然資源和生存機會.一般而言，在傳染病高發期，個體傾向于向傳染群的梯度方向擴散.基于此，本文主要研究一類帶空間擴散和非單調發病率的SIR傳染病模型的穩定性.

2 無擴散的SIR傳染病模型

設種群中的個體分為易感者，染病者和康復者三類，易感者由于與染病者接觸而染病，染病者康復后可能因缺少免疫力又變為易感者.設在t時刻易感者，染病者和康復者的數量分別為S(t)，I(t)和R(t)，則由Xiao和Ruan在文獻[6]中給出的具有非單調發病率的SIR傳染病模型如下：

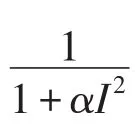
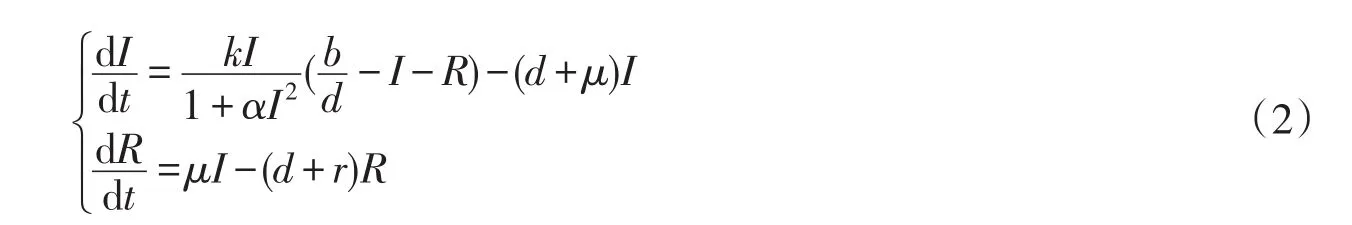
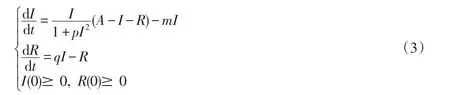
E0=(0,0)叫做無病平衡點，它是一個雙曲鞍點，表示傳染病的消失；E*=(I*,R*)叫做染病平衡點，表示染病者與康復者的并存.

定理2.1系統（3）的一切正解是最終有界的.

證明將系統（3）的兩個方程相加，并令W(t)=I(t)+R(t)，得

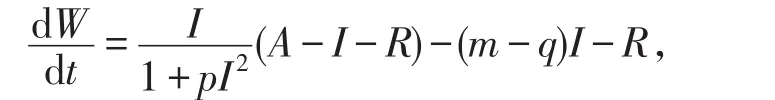
所以對任意的ε＞0，有下面的不等式

其中

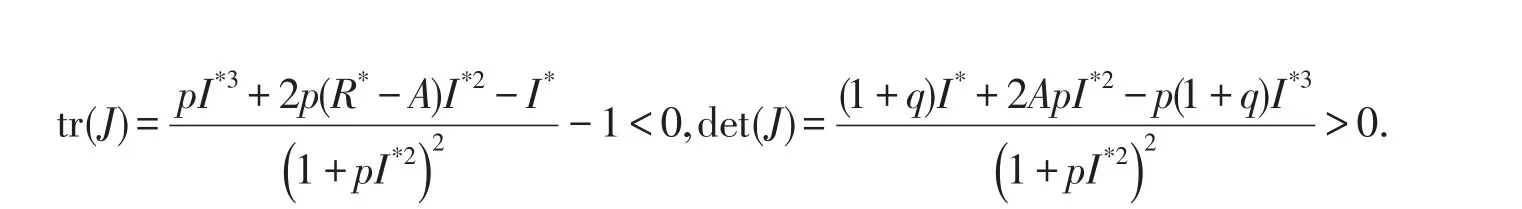
因此，由Roth-Hurwitz準則得到平衡點E*=(I*,R*)局部穩定的一個充分條件.

定理2.2系統（3）的染病平衡點E*=(I*,R*)是局部漸近穩定的.

事實上，更進一步地，我們有：

定理2.3系統（3）的染病平衡點E*=(I*,R*)在第一象限內是全局漸近穩定的.

證明構造Lyapunov函數

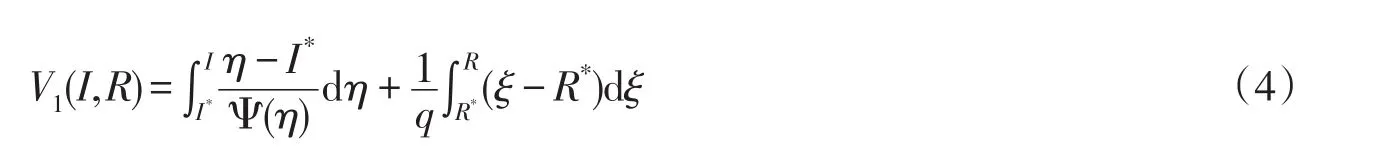
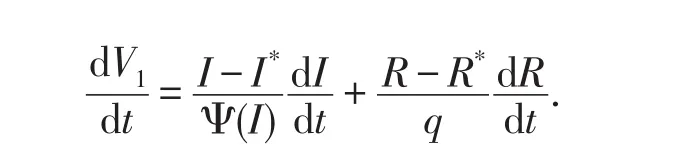
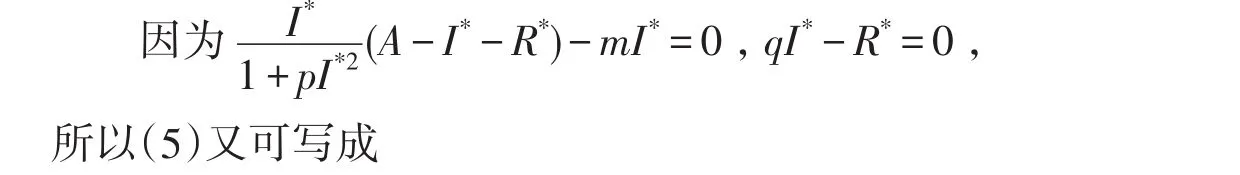
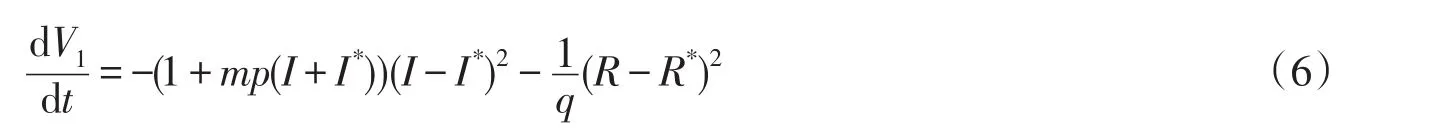
3 帶擴散的SIR傳染病模型

設易感者I和康復者R在空間中可以隨意移動，則與模型（3）對應的具有空間擴散的傳染病模型為

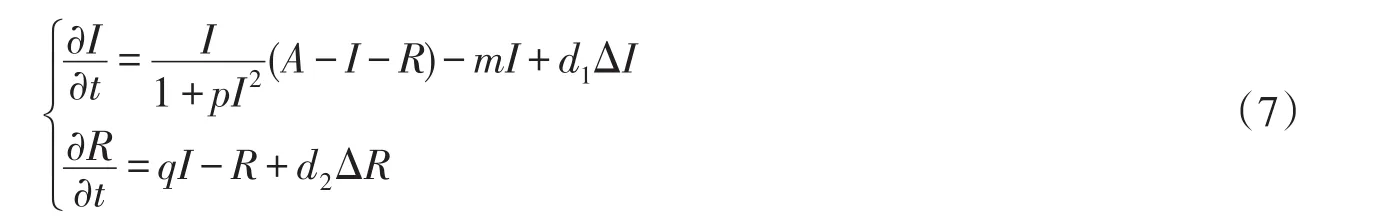
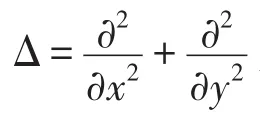
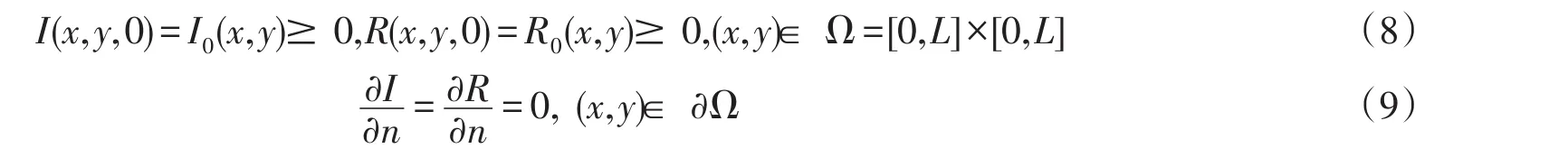
其中n表示邊界?Ω上的單位外法向量.齊次Neumann邊界條件說明上述系統是封閉的，在Ω的邊界上沒有個體移動.下面我們研究擴散系統（7）的相關性質，首先考察解的一致有界性.

定理3.1對于系統（7）的任一解() I(x,y,t),R(x,y,t)，有

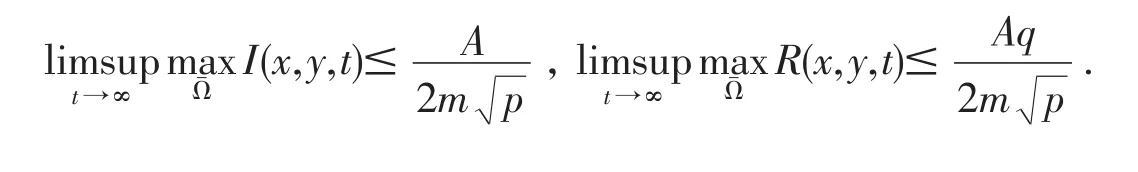
證明由系統（7）的第一個方程及條件（8）和（9）知，I(x,y,t)應滿足

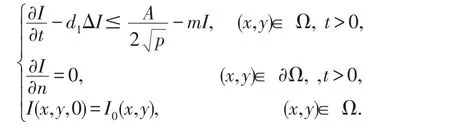
設X(t)是初值問題

證畢.

下面利用線性化方程的特征值以及Liapunov函數法討論系統（7）的染病平衡點E*=(I*,R*)的局部穩定性和全局穩定性.設0＜μ0＜μ1＜μ2＜…是算子Δ在具齊次Neumann邊界條件的Ω上的特征值，令集合

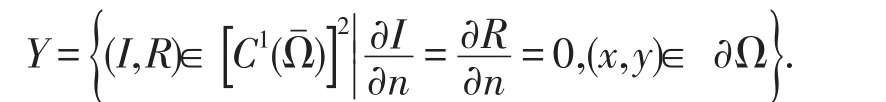
定理3.2系統（7）的染病平衡點E*=(I*,R*)是一致漸近穩定的.

證明系統（7）在平衡點E*處的線性化方程為

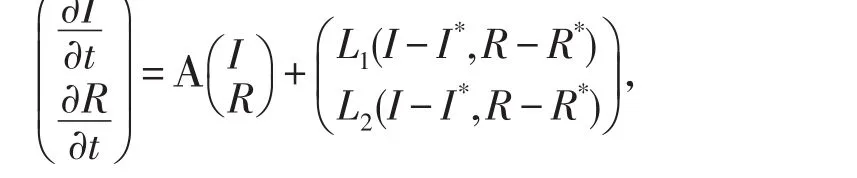
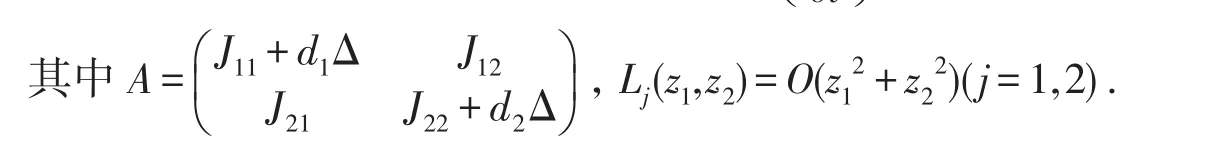
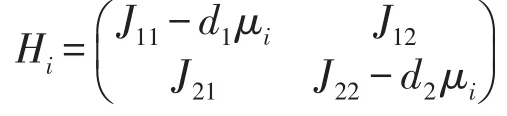
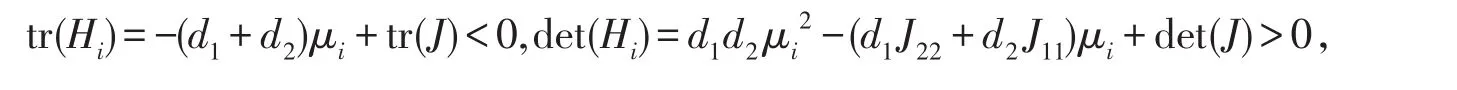
以上兩條說明，存在一個與i無關的正常數C，使得對所有的i都有Re()＜C，因此算子A的譜位于{Re(λ)＜C}中，由文獻[8]知，系統（7）的平衡點E*=(I*,R*)是一致漸近穩定的.

證畢.

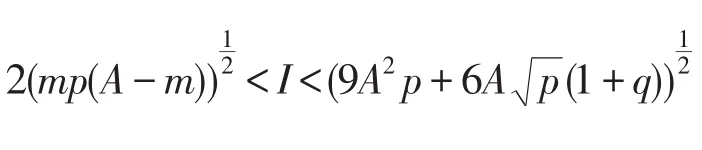
證明構造Lyapunov函數

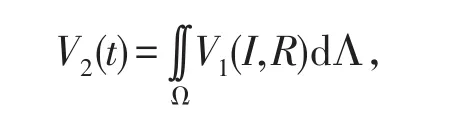
其中V1(I,R)的表達式如（4）式所示.將V2(t)沿著系統（7）的解關于時間t求導，得

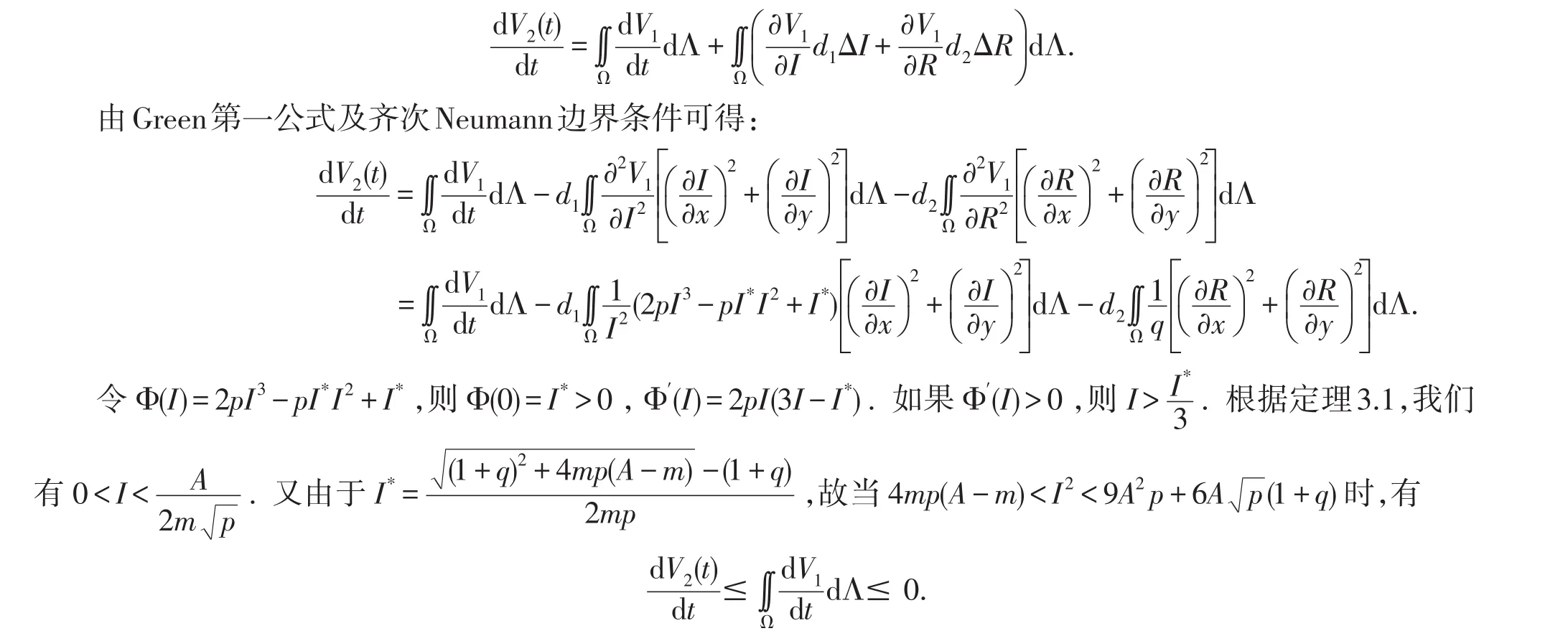
因此，系統（7）的平衡點E*=(I*,R*)是全局漸近穩定的.

證畢.

染病平衡點E*=(I*,R*)的全局漸近穩定性意味著，無論感染者和康復者空間擴散得快慢如何，傳染病將在一定空間內持久地存在.

[2]Holmes E,Lewis M,Banks J,et al.Partial differential equations in ecology:spatial interactions and population dynamics[J].Ecology,1994,75(1):17-29.

[3]Rass L,Radcliffe J.Spatial deterministic epidemics[M].Washington DC:American Mathematical Society,2003.

[4]Murray J.Mathematical biology[M].New York:Springer,2003.

[5]Wang K,Wang W,Song S.Dynamics of an HBV model with diffusion and delay[J].Journal of Theoretical Biology,2008,253(1):36-44.

[6]Xiao D,Ruan S.Global analysis of an epidemic model with nonmonotone incidence rate[J].Mathematical Bioscience,2007,208(2): 419-29.

[7]Pang P Y,Wang M X.Strategy and stationary pattern in a three-species Predator-Prey model[J].Journal of Differential Equations, 2004,200(2):245-273.

[8]Henry D.Geometric theory of semilinear parabolic equations[M].In:Lecture Notes in Mathematics.New York:Springer-Verlag, 1981.

[1]Kermack W O,McKendrick A G.A Contribution to the Mathematical Theory of Epidemics[J].Proc Roy Soc,1927,115(772):700-721.

Stability Analysis of an SIR Epidemic Model with Diffusion

ZHU Dao-yu
(School of Science,Guizhou Minzu University,Guiyang 550025,China)

An SIR epidemic model with spatial diffusion is investigated.Local stability of the endemic equilibrium of the epidemic model is presented by analyzing eigenvalues corresponding to linearization equation.A sufficient condition is obtained for the global asymptotic stability of the endemic equilibrium by Lyapunov function method.

O29

A

1008-2794（2012）10-0045-06

2012-09-27

貴州民族大學校級科研基金資助項目（201202）

朱道宇（1982—），女，貴州遵義人，講師，碩士，研究方向：微分方程與動力系統.

Key words:epidemic model;equilibrium;asymptotic stability