一類新超混沌系統的同步與反同步

張樹來

（常熟理工學院數學與統計學院，江蘇常熟 215500）

一類新超混沌系統的同步與反同步

張樹來

（常熟理工學院數學與統計學院，江蘇常熟 215500）

以一類新超混沌系統為例，研究了驅動系統和響應系統的同步與反同步問題，利用Lyapunov穩定性理論設計了控制器，實現了它們的同步與反同步，數值模擬結果驗證了該方法的有效性.

超混沌系統；Lyapunov函數；同步；反同步

從1963年Lorenz在實驗中發現第一個混沌吸引子以來，Lorenz系統就被作為第一個研究混沌的物理和數學模型，成為后人研究混沌理論的出發點和基石.在過去的幾十年里，混沌控制與同步的理論在一些工程領域中得到了廣泛的應用，如圖像加密，保密通信和信息工程等，顯示出了重要的應用價值[1-2]，所以對混沌控制與同步的理論研究已成為非線性控制理論研究的熱點之一.由于混沌系統對初值極其敏感性，所以長期以來人們認為混沌系統是不可控制的，混沌同步就更加難以實現.自從Pecora和Carroll[3]在1990年利用電路實現混沌同步以來，混沌同步受到了各個領域學者的廣泛關注.隨著混沌控制與同步研究的不斷深入，如廣義同步、完全同步、耦合同步和超混沌系統同步方案[4-7]，近來又提出了混沌系統的反同步[8]等.

目前對于混沌控制與同步研究方法很多，但是對于超系統之間的同步與反同步研究相對較少，在實際應用中特別是兩個超混沌系統的同步與反同步容易應用于安全通信中，因此考慮兩個超混沌系統的同步與反同步更具有重要的實用價值.本文利用Lyapunov的理論設計了相應的控制器，實現了兩個超混沌系統的同步與反同步，并利用matlab工具進行了數值仿真，驗證了其有效性.

1 系統模型

最近，T.Wang等人研究了一類新的四維超混沌系統[8]，系統如下：

這里x1,x2,x3和x4為變量，a,b,c,d為參數.當a=2.1,b=0.6,c=30,d=0.7時，（1）為超混沌系統.圖1為超混沌系統（1）的吸引子.

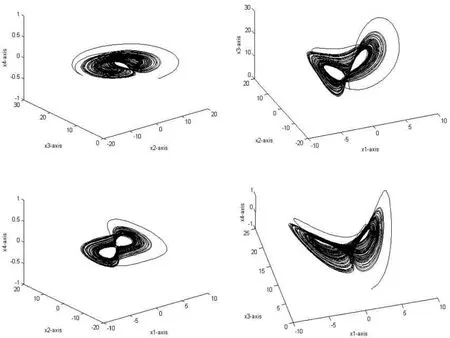
圖1 當a=2.1,b=0.6,c=30,d=0.7時超混沌系統（1）的吸引子

2 驅動系統和響應系統的同步及數值仿真

將系統（1）作為驅動系統，相應地響應系統為：

此處ui(i=1,2,3,4)為控制器.令系統（1）與系統（2）的同步誤差為：

我們構建Lyapunov函數為：

故

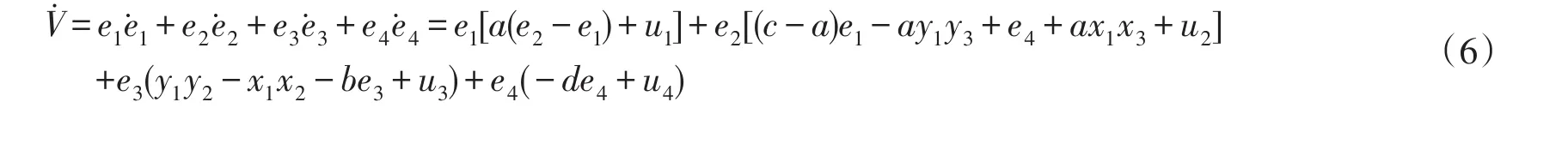
此時若取

即在控制器（7）的作用下，兩個超混沌系統對應的時間序列可以達到同步.采用Runge-Kutta方法模擬，驅動系統和響應系統初值選為：x1(0)=100,x2(0)=5，x3(0)=100,x4(0)=-10，y1(0)=30,y2(0)=20,y3(0)=20,y4(0) =8，數值模擬得誤差隨時間變化如圖2所示.由圖2可見，e1,e2,e3,e4很快趨于0，系統達到了同步.

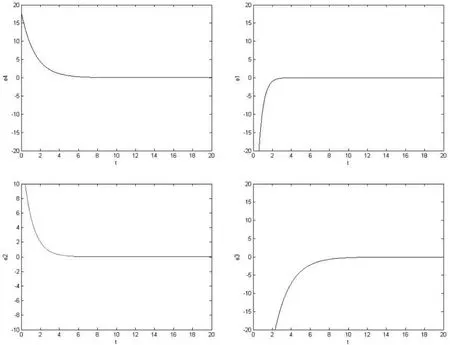
圖2 系統（1）與（2）對應時間序列同步誤差曲線

3 驅動系統和響應系統的反同步及數值仿真

仍然將系統（1）作為驅動系統，（2）為響應系統，令系統（1）與系統（2）的同步誤差為：

構建（5）式的Lyapunov函數，則

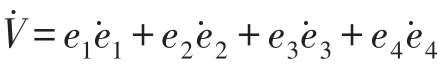
即在控制器（10）的作用下，驅動系統（1）與響應系統（2）達到了反同步.采用四階Runge-Kutta方法模擬，驅動系統和響應系統初值選為：x1(0)=-10,x2(0)=-5，x3(0)=10,x4(0)=-10，y1(0)=21,y2(0)=20,y3(0)= 8,y4(0)=-9，數值模擬得誤差隨時間變化如圖3所示.由圖3可見，e1,e2,e3,e4很快趨于0，系統達到了同步.

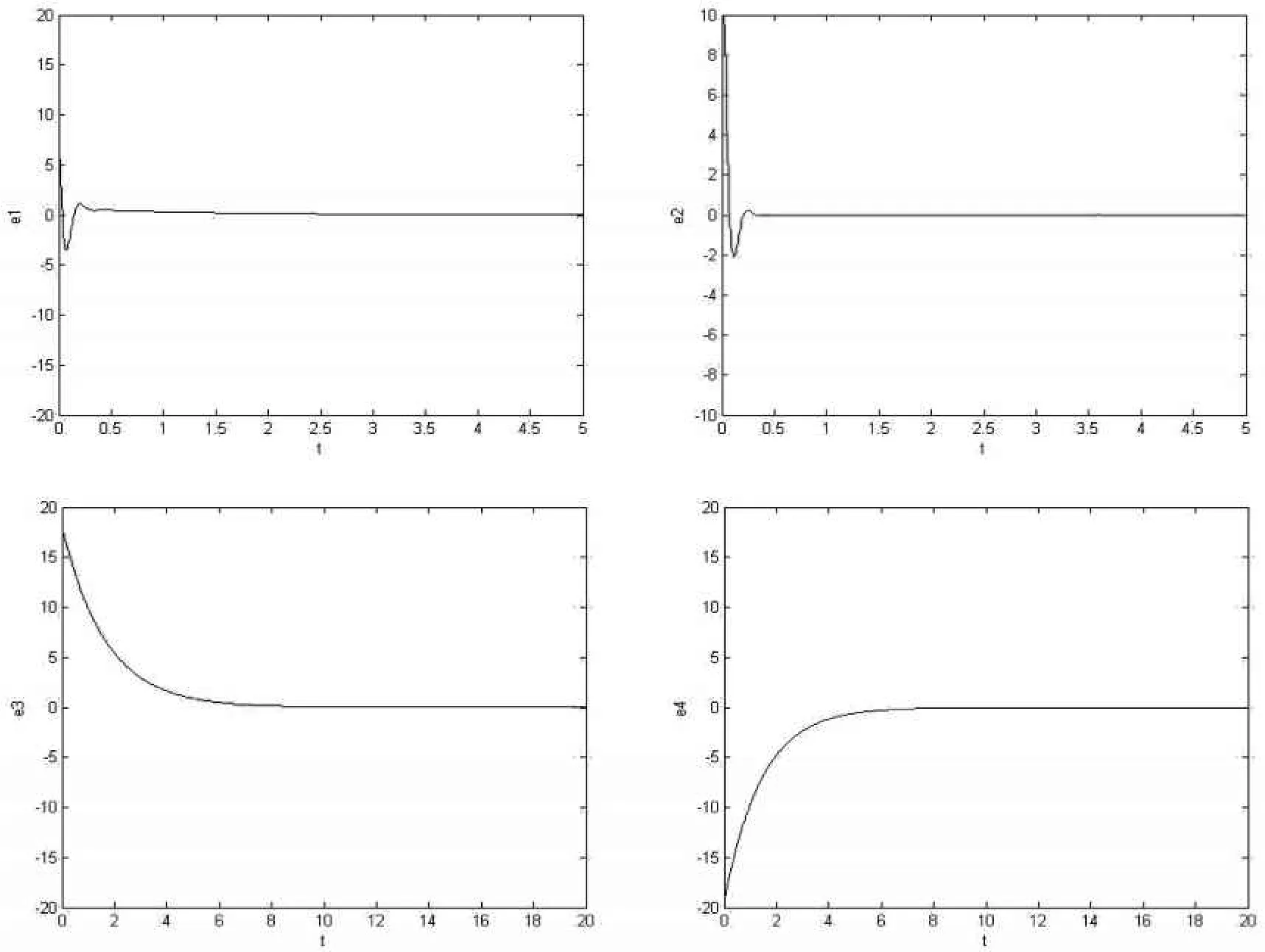
圖3 系統（1）與（2）對應時間序列反同步誤差曲線

4 結論

本文首先介紹了混沌及同步方法的內容，然后主要利用Lyapunov穩定性理論，根據實際情況設計了適當的控制器，對一類新的四維超混沌系統[9]與其對應響應系統的時間序列同步與反同步進行了研究，并利用matlab等工具進行了數值仿真，驗證了其可行性與有效性.由于該方法設計的控制器比較簡單，因而在實際工程應用中更容易實現，具有一定的應用價值.

[2]Park J H.On synchronization of unified chaotic systems via nonlinear control[J].Chaos Solitons Fract,2005,25:699-704.

[3]Pecora L M,Carroll T L.Synchronization in chaotic systems[J].Phys Rev Letter,1990,64(8):821-824.

[4]張樹來，吳志明.一個新時變混沌系統的耦合同步[J].常熟理工學院學報，2007，21（10）：24-28.

[5]Mahmoud G M,Mahmoud E E.Complete synchronization of chaotic complex nonlinear systems with uncertainparameters[J].Nonlinear Dyn,2010,62:875-882.

[6]Kocarev L,Parlitz U.General Approach for Chaotic Synchronization with Applications to Communication[J].Phys Rev Lett,1995, 74(6):5028-5031.

[7]于靈慧，房建成.Hénon混沌同步的自適應逆控制[J].控制理論與應用，2005，22（4）：623-626.

[8]Kim C M,Rim S W,Kye W H,et al.Anti-synchronization of chaotico scillators[J].Physics Letters A,2003,320(1):39-46.

[9]Wang T,Jia N.Chaos control and hybrid projective synchronization of several new chaotic systerms[J].Applied Mathematics and Computation,2012,218:7231-7240.

[1]Zhang D,Xu J.Projective synchronization of different chaotic time-delayed neural networks based on integral sliding mode controller[J].Appl Math Comput,2010,217:164-171.

Synchronization and Anti-synchronization in a Class of New Hyper-chaotic System

ZHANG Shu-lai
(School of Statistics and Mathematics,Changshu Institute of Technology,Changshu 215500,China)

In this paper,the definition of chaos is introduced,and these methods of chaotic synchronization are recommended.Then,as an example of a class of new hyper-chaotic system,chaos synchronization and anti-synchronization of the drive system and the slave system are investigated.With the Lyapunov stability theory,the controller is constructed analytically to synchronize and anti-synchronize them.The numerical simulation results show that the proposed scheme is effective.

TP273；O415.5

A

1008-2794（2012）10-0032-05

2012-09-11

常熟理工學院青年教師科研啟動基金資助項目“一類混沌系統的控制與同步”（QZ1204）

張樹來（1978—），男，山東臨沂人，講師，碩士，研究方向：混沌動力學．

Key words:hyper-chaotic system;Lyapunov function;synchronization;anti-synchronization