Spectrum-generating超代數的一類子代數的研究

郭娜，劉東，高壽蘭

（1.杭州電子科技大學理學院，浙江杭州 310000；2.湖州師范學院理學院，浙江湖州 313000）

Spectrum-generating超代數的一類子代數的研究

郭娜1，劉東2，高壽蘭2

（1.杭州電子科技大學理學院，浙江杭州 310000；2.湖州師范學院理學院，浙江湖州 313000）

研究spectrum-generating超代數的一類子代數，確定了這類子代數的低階上同調群以及自同構群.這類子代數對于討論N=2-超共形代數上Harish-Chandea模的分類很有意義.

李超代數；導子代數；中心擴張；自同構

1 引言

超共形代數與共形場論和弦理論緊密聯系，在數學與物理學有重要作用.N=2-超共形代數[1]是復維數-D的Calabi-Yau流形上的弦緊致分析的基本工具[2].它的表示理論和Kac-Roan-Wakimoto猜想有關[3].為了對N=2-超共形代數上的Harish-Chandra模進行分類，我們需要研究下面的李超代數，它是Spectrum-generating超代數的一個子代數[4].

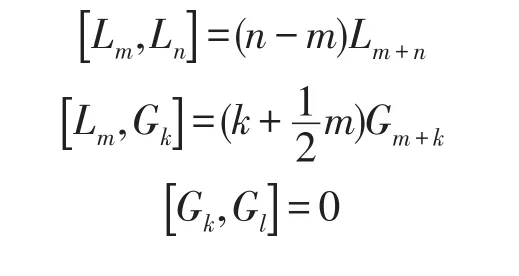
本文重點討論李超代數A的結構理論，包括它的導子代數、二上同調群、自同構群等.我們分別用C，Q 和Z來定義復數集、有理數集和整數集.對于任意集合S，定義它的非零元素集合為S*.

2 泛中心擴張

首先我們回顧李超代數L上的二上循環，它是C-雙線性函數：ψ：L×L→C并且滿足下面的關系式：

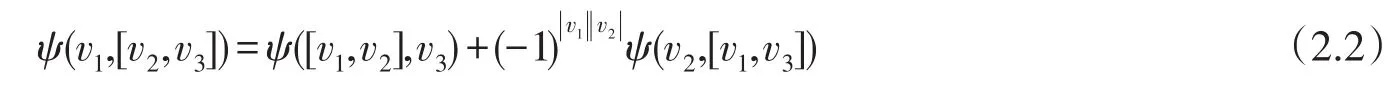
對任意的v1,v2,v3∈L，定義L上的二上循環的向量空間為C2(L,C).

對任意的C-線性函數f：L→C，定義二上循環ψf如下：對任意的v1,v2∈L，ψf(v1,v2)=f([v1,v2]).

這樣的二上循環我們稱為L上的二上邊界或者平凡二上循環.

定義L的二上邊界的向量空間為B2(L,C).如果φ-ψ是平凡的，那么我們稱二上循環φ與二上循環ψ是等價的.對于一個二上循環ψ，定義它的等價類為[ψ].商空間H2(L,C)=C2(L,C)/B2(L,C)=｛二上循環的等價類｝，被稱為L的二階上同調群.

眾所周知，Virasoro循環的二上循環由下式確定：

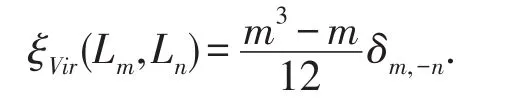
定理1dimH2(A,C)=2，其中關于A的常見的不平凡二上循環如下：

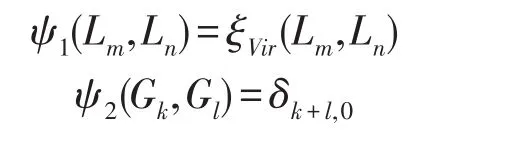
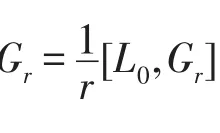
令φ=ψ-ψf-ξVir，其中ψf滿足ψf(v1,v2)=f([v1,v2]).那么我們得到φ(Lm,Ln)=0對任意的m,n∈Z成立.

定理1可由下面的引理1-3得到.

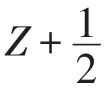
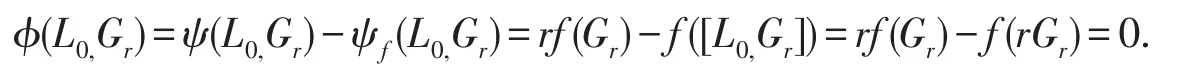
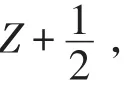
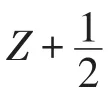
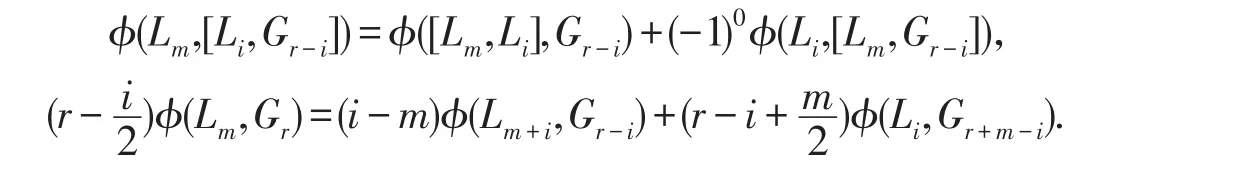
令i=0，即

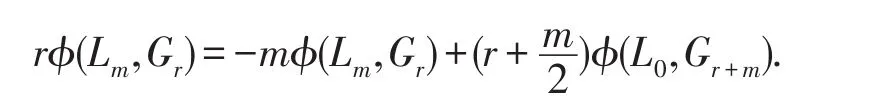
由于φ(L0,Gr+m)=0，那么(r+m)φ(Lm,Gr)=0.

因為r+m≠0，所以φ(Lm,Gr)=0.

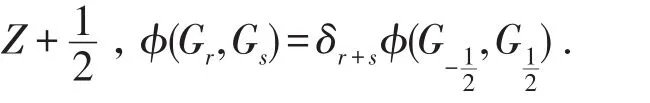
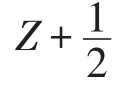
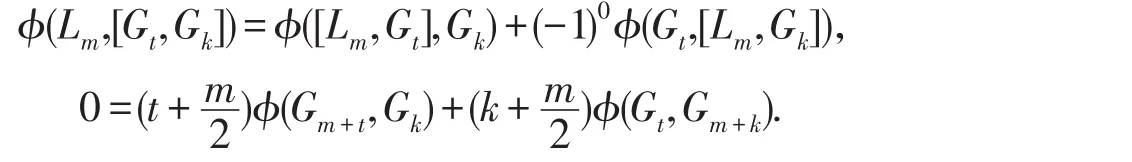
令m=-2t，就得到如果t+k≠0，φ(Gt,Gk)=0.

令t=-(k+m)，

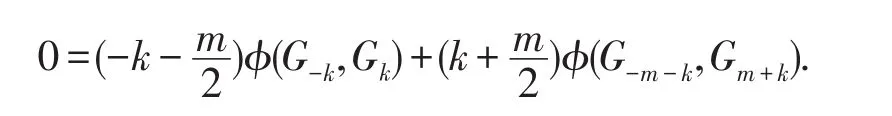
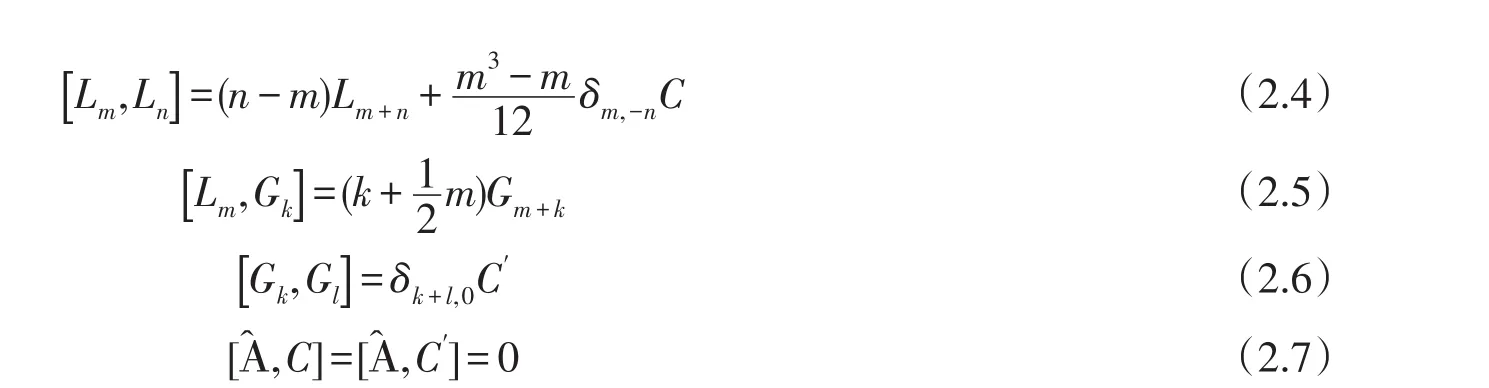
3 算子Lm,Gk的構造

本節中，當C=C′=1時，我們利用一些算子去構建上述李超代數A^.

我們利用Fermionic振子ψn，并且它滿足反交換關系

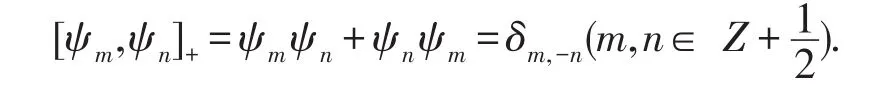
上述代數可以由下面的向量空間表示：

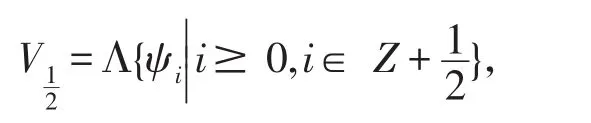
其中符號Λ表示由ψi生成的外代數.

令Lk(k∈Z)是Vδ中的算子，定義：

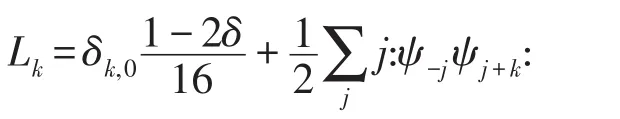
其中j跑遍δ+Z并且正常序列定義為

那么：

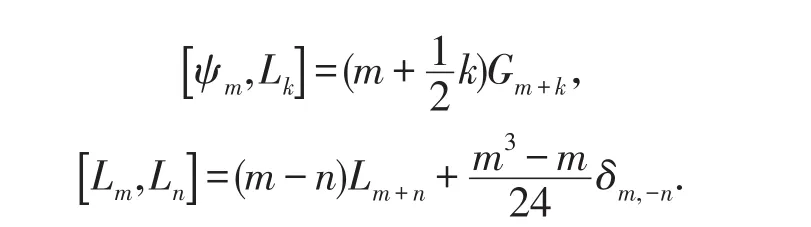
所以為了構建這個代數，我們僅需要將ψk替換為Gk，那么關系式（2.4）-（2.7）成立.

4 李超代數A的導子

令V是一個A-模.從A到V的線性映射φ叫做導子，如果對任意的x,y∈A，我們有

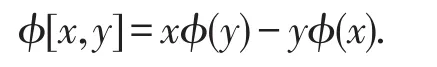
當v∈V，映射φ:x→x·v叫做內導子.所有導子的向量空間定義為Der(A,V).所有內導子的向量空間定義為Inn(A,V).那么在V中的A的一階上同調群和它們的系數關系為等式右邊同時也叫做外導子空間.

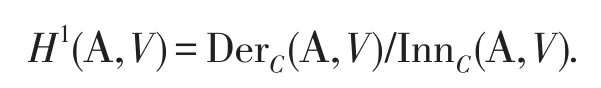
首先我們介紹A的外導子δ：

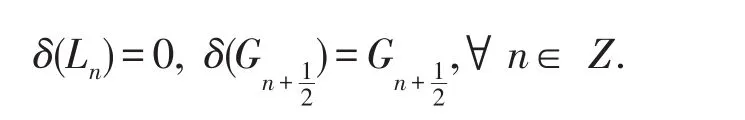
引理4Der(A,V)=Der(A,V)0+Inn(A,V)，其中Der(A,V)0={D∈Der(A,V)|D(Ln)?Vn,對任意的n∈Z}.

證明從文獻[5]很容易得到（證明略）.

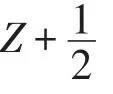
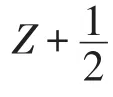
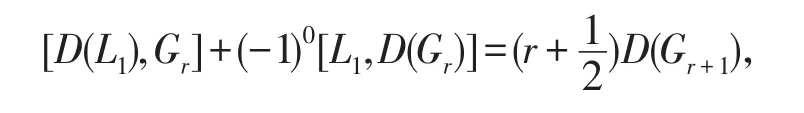
那么

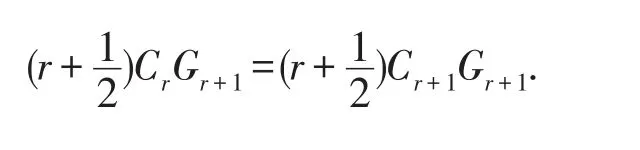
比較Gr+1的系數，我們有

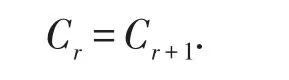
從引理4和引理5，我們可以得到下面的結論.

定理2

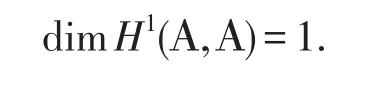
5 自同構群

定義AutA為自同構群.我們知道，對任意的σ∈AutA，σ(Liˉ)=Liˉ，iˉ∈Z2.

定理3令σ∈AutA，則存在a,b∈C*和ε∈{±1}滿足

反之，如果σ是A上的一個線性函數滿足（5.1）-（5.3），ε∈{±1}和a,b∈C*，那么σ∈AutA.

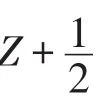
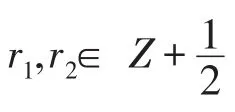
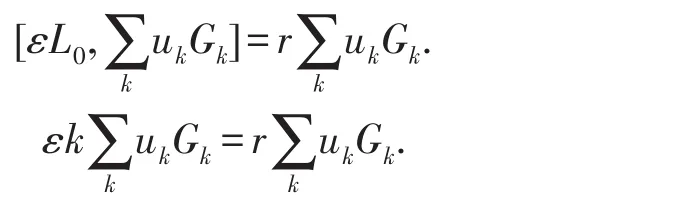
比較Gk的系數，得到εk=r.因此，

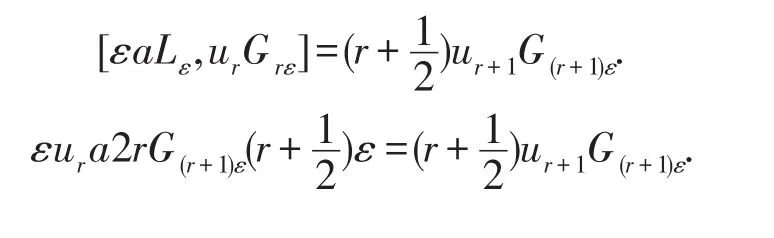
比較G(r+1)ε的系數，則aur=ur+1.

所以假設

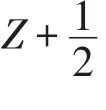
定義A的自同構為σ(ε,a,b)滿足（5.1）-（5.3），那么

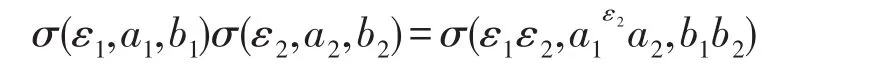
和

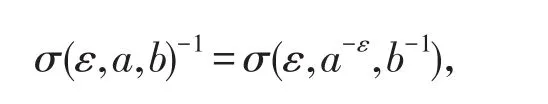
當且僅當ε1=ε2,a1=a2,b1=b2.

通過上面的討論，我們很容易得到下面的定理：

定理4AutA=Z2∝(C*×C*)

[1]Dobrev V K.Characters of the unitarizable highest weight modules over the N=2 superconformal algebras[J].Phys Lett,1987,B (186):43-51.

[2]Eguchi T,Hikami K.N=2 superconformal algebra and the entropy of Calabi-Yau manifolds[J].Lett Math Phys,2010,92(3):269-297.

[3]Arakawa T.Representation theory of superconformal algebras and the Kac-Roan-Wakimoto conjecture[J].Duke Math J,2005,130 (3):435-478.

[4]Ademollo M,Brink L,Adda A D,et al.Supersymmetric strings and colour confinement[J].Phys Lett,1976,B(62):105-110.

[5]Farnsteiner R.Derivations and central extensions of finitely generated graded Lie algebra[J].J Algebra,1998,118:33-45.

[6]Fuks D B.Cohomology of Infinite-Dimensional Lie Algebras[M].New York:Springer,1986:119-120.

A Study of One Subalgebra of the Spectrum-generating Superalgebra

GUO Na1,LIU Dong2,GAO Shou-lan2
(1.Depaprtment of Sciences and Mathematics,Hangzhou Dianzi University,Hangzhou 310000,China;2.Department of Sciences and Mathematics,Huzhou Teachers College,Huzhou 313000,China)

One subalgebra of spectrum-generating superalgebra is studied in this paper.And low order cohomology group and the automorphism group of this algebra are also determined in the paper.This subalgebra is helpful to classified Harish-Chandea modules over the N=2 superconformal algebra.

Lie superalgebra;derivation algebra;central extensions;automorphism

O152.5

A

1008-2794（2012）10-0027-05

2012-08-21

國家自然科學基金項目“Virasoro代數及相關代數的結構與表示理論”（11071068）；國家自然科學基金項目“共型流李代數的結構和表示”（11201141）；浙江省自然科學基金項目“Virasoro型李代數與頂點算子代數的研究”（Y6100148）；浙江省自然科學基金項目“無限維李代數與頂點算子（超）代數的結構域表示”（LQ12A01005）

郭娜（1986—），女，河南南陽人，杭州電子科技大學2010級研究生，研究方向：李代數.